Master 2 Variable Equations: Free Worksheet Included

Learning to solve systems of linear equations in two variables is a critical skill in algebra that helps in understanding complex relationships between variables. This post will guide you through various methods for solving these equations, provide tips for efficient calculation, and includes a free, interactive worksheet to test your skills.
Understanding Systems of Linear Equations
At its core, a system of linear equations involves finding the values of variables that make all equations in the system true at the same time. Here’s what you need to know:
- Each equation in the system represents a line on a coordinate plane.
- The solution to the system is the point or points where these lines intersect.
- Systems can have:
- One unique solution
- Infinite solutions (lines coincide)
- No solution (lines are parallel)
Methods to Solve Two-Variable Equations
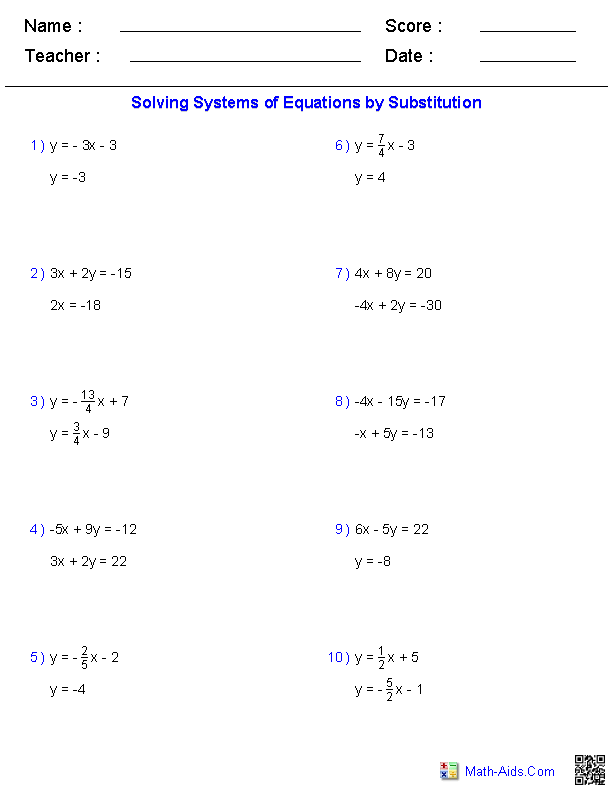
There are several methods to solve systems of linear equations:
- Graphing Method: Plot the lines on a graph and find the intersection point.
- Substitution Method: Solve one equation for one variable and substitute into the other equation.
- Elimination Method: Multiply equations by necessary numbers so that adding or subtracting eliminates one variable.
- Matrix Method: Use matrices to solve complex systems.
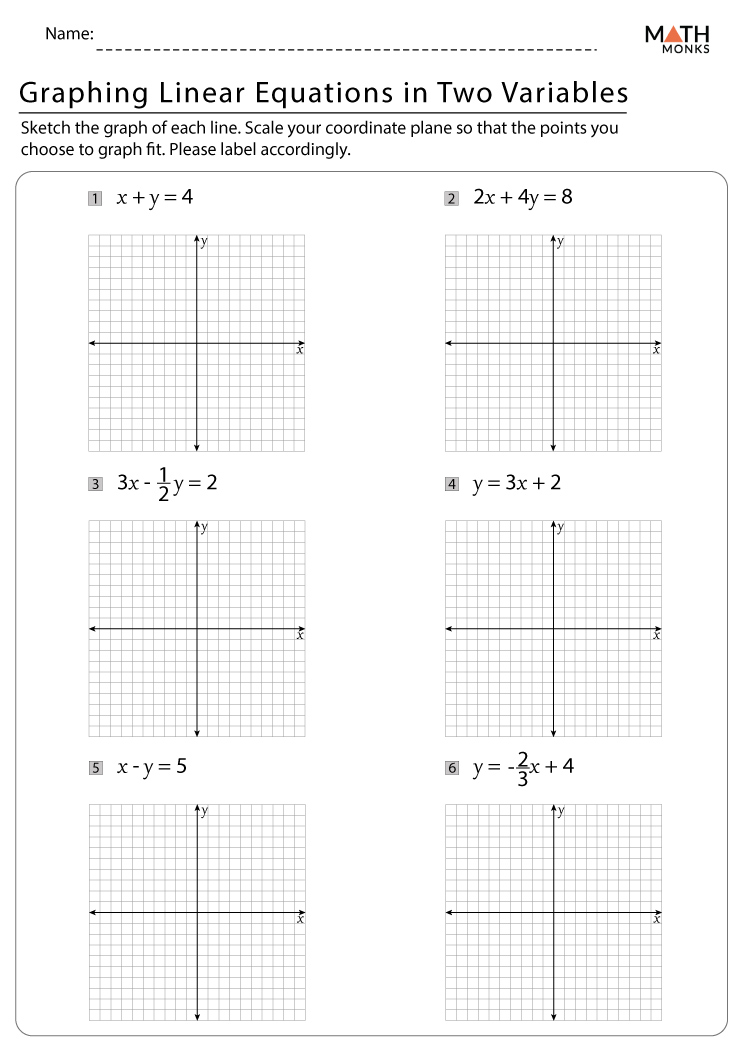
Graphing Method

The graphical approach involves plotting the equations on a graph. Here’s how:
- Plot each equation as a line.
- The point where these lines cross is your solution.
- If lines are parallel, there’s no solution. If lines are the same, infinite solutions exist.
This method is particularly useful for visualizing the solution but can be less accurate for exact solutions.
Substitution Method

Here’s a step-by-step guide:
- Choose one equation and solve for one of the variables in terms of the other.
- Substitute this expression into the other equation.
- Solve the resulting equation to find the value of the remaining variable.
- Back-substitute to find the other variable.
📘 Note: This method is especially efficient when one equation has a variable with a coefficient of 1 or -1.
Elimination Method

Follow these steps:
- Align the equations vertically so like terms are in columns.
- Multiply or divide equations by necessary constants to eliminate one of the variables.
- Add or subtract the equations to cancel out one variable.
- Solve for the remaining variable, then back-substitute to find the other.
Here’s an example:
| Equation 1 | Equation 2 |
|---|---|
| 2x + 3y = 11 | 4x - y = 7 |

By making the coefficient of y the same (multiply the second equation by 3), we can then subtract to eliminate y and solve for x.
Matrix Method

This method involves:
- Expressing the system in matrix form.
- Using operations like row reduction to find the solution.
While more advanced, this approach is particularly useful for solving larger systems or those with many variables.
Interactive Worksheet
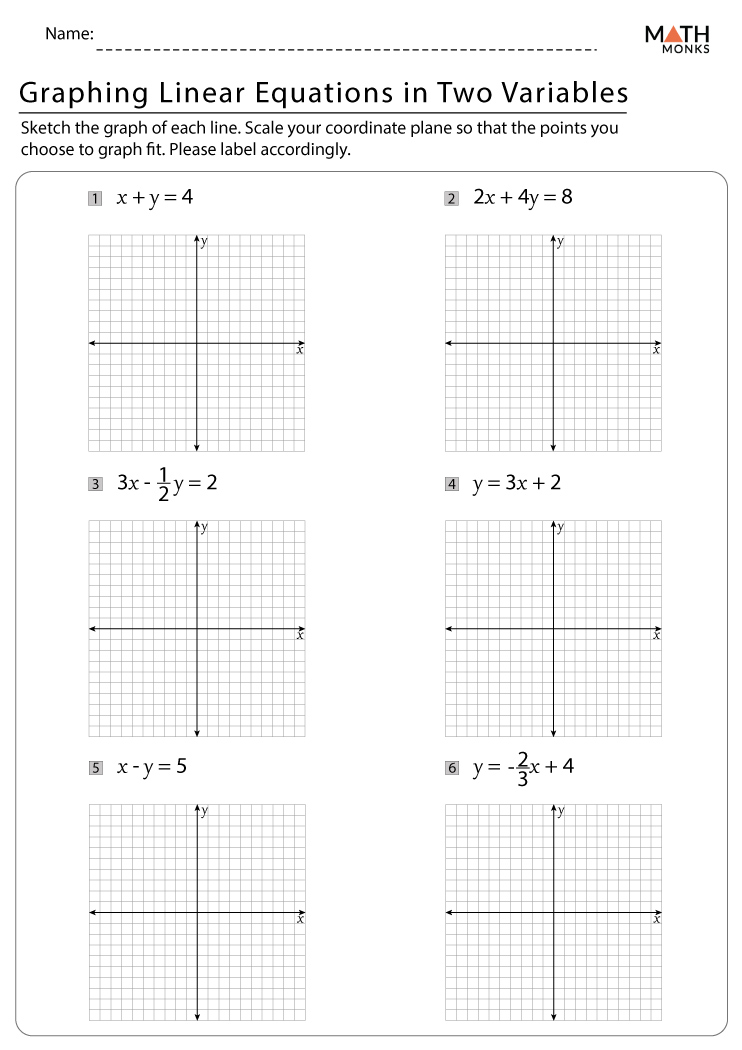
To reinforce your understanding, we’ve provided an interactive worksheet where you can practice all the methods discussed above. This worksheet includes:
- Solve by graphing: plot lines on a graph.
- Solve by substitution: step-by-step questions.
- Solve by elimination: variable elimination exercises.
- Matrix method questions: solve small systems.
Engage with these problems to solidify your grasp on solving systems of equations.
Through understanding these methods, not only will you become proficient in solving linear equations but also gain insight into algebraic structures and patterns. Remember, choosing the right method depends on the structure of the equations you're dealing with.
Why do we use systems of equations?

+
Systems of equations are used to solve real-world problems where multiple conditions or constraints are present. They help in finding where variables intersect, offering solutions that satisfy all given conditions simultaneously.
Can systems of equations have more than two variables?

+
Yes, systems can have any number of variables. The methods described here can be adapted for systems with more than two variables, though they become more complex as the number of variables increases.
What if I solve for a variable and get a contradiction?

+
If you encounter a contradiction, such as 0 = 5, it indicates that the system has no solution, meaning the lines are parallel and never intersect.
How do I know when to use the substitution versus elimination method?

+
Use substitution when one equation easily solves for one variable or when variables have a coefficient of 1 or -1. Choose elimination when the equations have common coefficients that allow for easy cancellation of a variable.
Can graphing always give an accurate solution to a system of equations?

+
No, graphing might provide an approximate solution due to limitations in scale and precision. For exact solutions, algebraic methods like substitution or elimination are more accurate.



