7 Key Angle Pair Relationships Worksheet Answers
Exploring angle pair relationships is crucial for students aiming to master geometry. Understanding these relationships not only enhances one's ability to solve complex problems but also provides insights into how shapes interact within a two-dimensional plane. This comprehensive guide will explore the 7 key angle pair relationships, their definitions, properties, and how to solve related problems effectively.
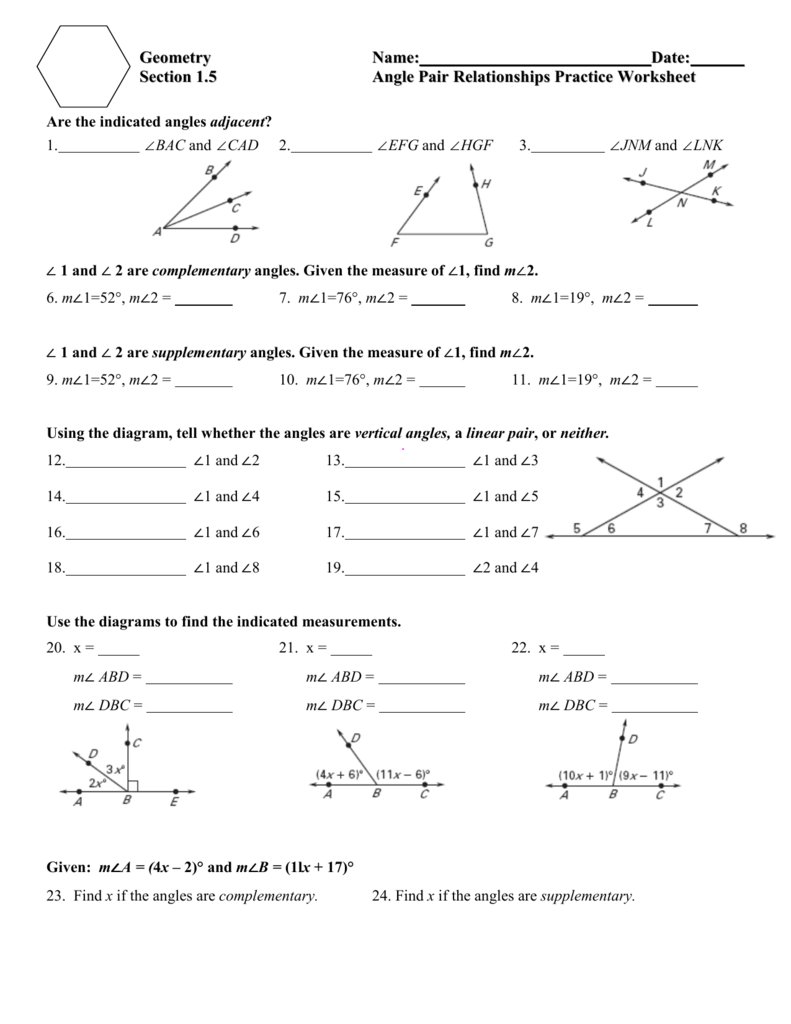
1. Complementary Angles

Complementary angles are two angles whose sum equals 90°. Here are the key points to remember:
- When two angles are complementary, they can form a right angle together.
- If one angle measures a degrees, the other complementary angle will measure (90 - a) degrees.
💡 Note: Both angles need to be positive and less than 90° to be complementary.
2. Supplementary Angles
Supplementary angles, on the other hand, add up to 180°. Here’s what you should know:
- These angles can form a straight line when placed adjacently.
- If one angle is b degrees, its supplementary angle will be (180 - b) degrees.
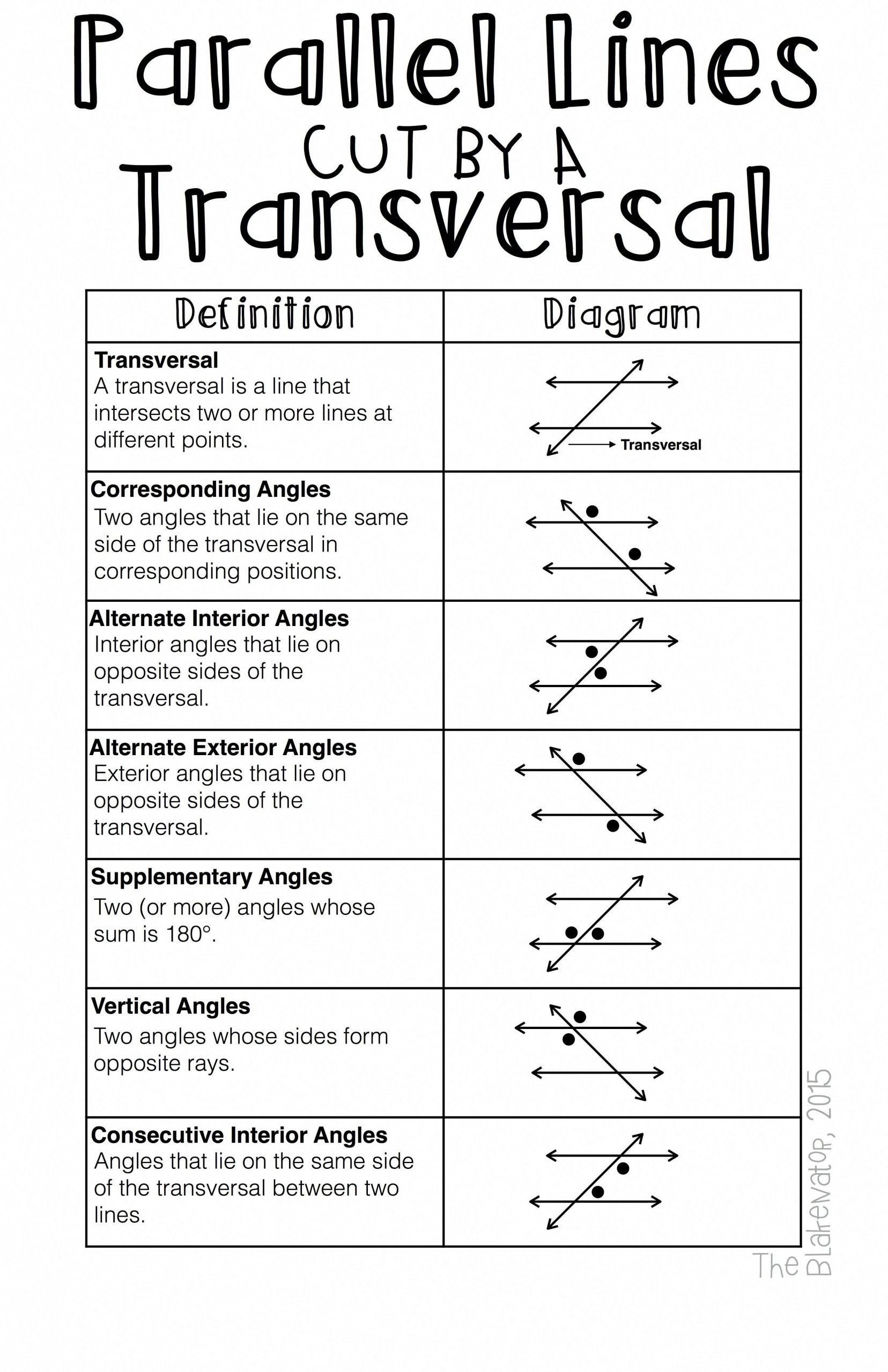
3. Vertical Angles
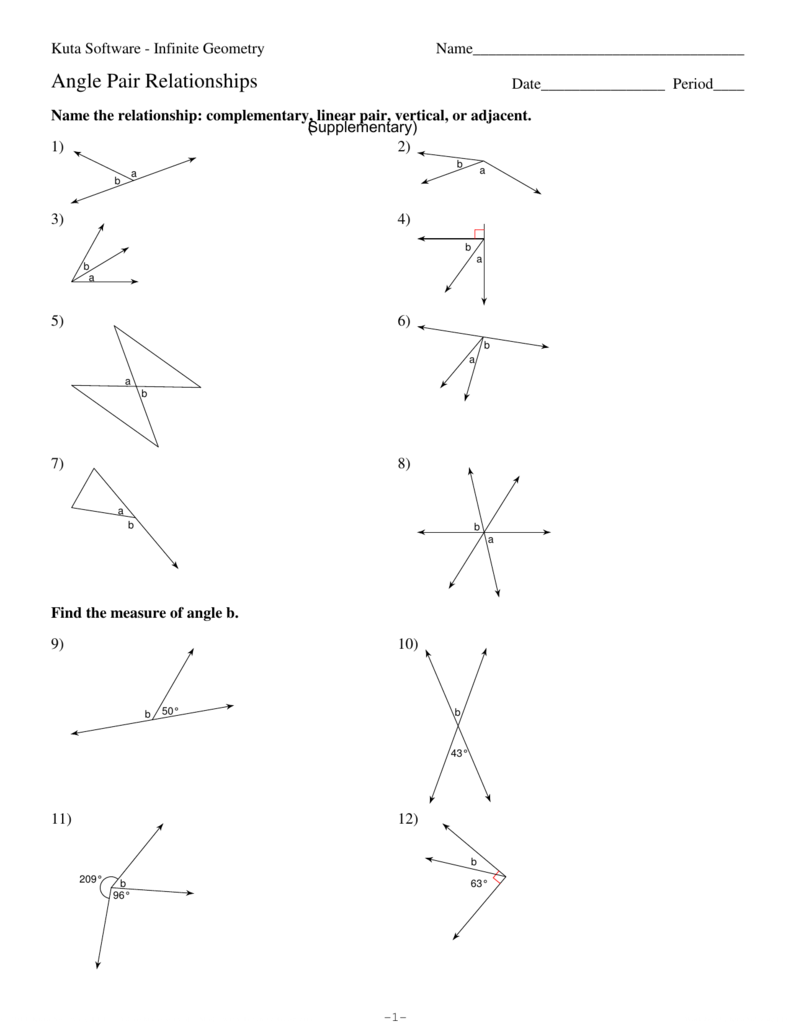
When two lines intersect, they create four angles. The pairs of opposite angles are called vertical angles, and they:
- Are equal in measure.
- Are formed by the intersection of two lines.
4. Adjacent Angles

Adjacent angles share a common side and vertex, but do not overlap. Here are the characteristics:
- They have a common endpoint and a common side.
- They are next to each other without overlapping.
5. Linear Pair Angles
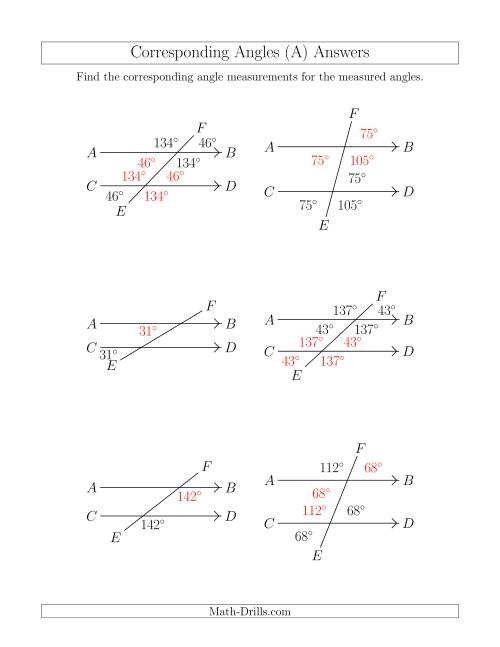
A linear pair is a pair of adjacent angles formed when two lines intersect, where:
- The angles are supplementary.
- Their non-common sides form a straight line.
6. Alternate Interior Angles

These angles are formed inside the parallel lines when cut by a transversal:
- If the lines are parallel, these angles are congruent.
- They lie on opposite sides of the transversal.
7. Alternate Exterior Angles
Alternate exterior angles occur outside the parallel lines and are:
- Equal in measure if the lines are parallel.
- Found on opposite sides of the transversal.
Identifying and Solving Angle Pair Problems

When working with angle pair relationships, here's how you can identify and solve problems:
- Identify the relationships: Look at the diagram and identify which angles form pairs based on the above descriptions.
- Use known angles: If some angles are known, use the relationships to find the unknowns. For example, if one angle is 40° in a linear pair, the other must be 140°.
- Set up equations: Use the sum properties to set up equations. For example, if two angles are supplementary, their sum equals 180°.
- Solve for unknowns: Solve the equations to find the measures of the unknown angles.
💡 Note: Remember that geometric properties are absolute. If a statement about angles seems not to follow these rules, recheck your identification or calculation.
Worksheet Answers Example

Let's solve a few common worksheet problems to illustrate the application of these relationships:
| Question | Answer |
|---|---|
| Find the measure of angle y if the adjacent angle is 75°. | Angle y is supplementary to 75°. Therefore, y = 180° - 75° = 105°. |
| If ∠A and ∠B are vertical angles and ∠A is 32°, what is the measure of ∠B? | Since vertical angles are equal, ∠B = 32°. |
| Given two parallel lines cut by a transversal with ∠1 = 68°, find the measure of its alternate interior angle, ∠7. | Alternate interior angles are equal, so ∠7 = 68°. |

In summary, understanding angle pair relationships is pivotal for solving geometric problems. These relationships help us navigate the intricate world of angles and lines, providing a clear framework to understand how shapes interact. By mastering these concepts, one can unlock the door to more advanced geometric studies and applications.
What’s the difference between complementary and supplementary angles?

+
Complementary angles add up to 90°, while supplementary angles add up to 180°.
Can vertical angles be adjacent?
+
No, vertical angles are opposite angles formed by two intersecting lines; they never share a common side, thus they can’t be adjacent.
How do you know if two angles form a linear pair?

+
Two angles form a linear pair if they are adjacent and their non-common sides form a straight line, making their sum 180°.