Y Mx B Worksheet Answers: Quick Guide for Students
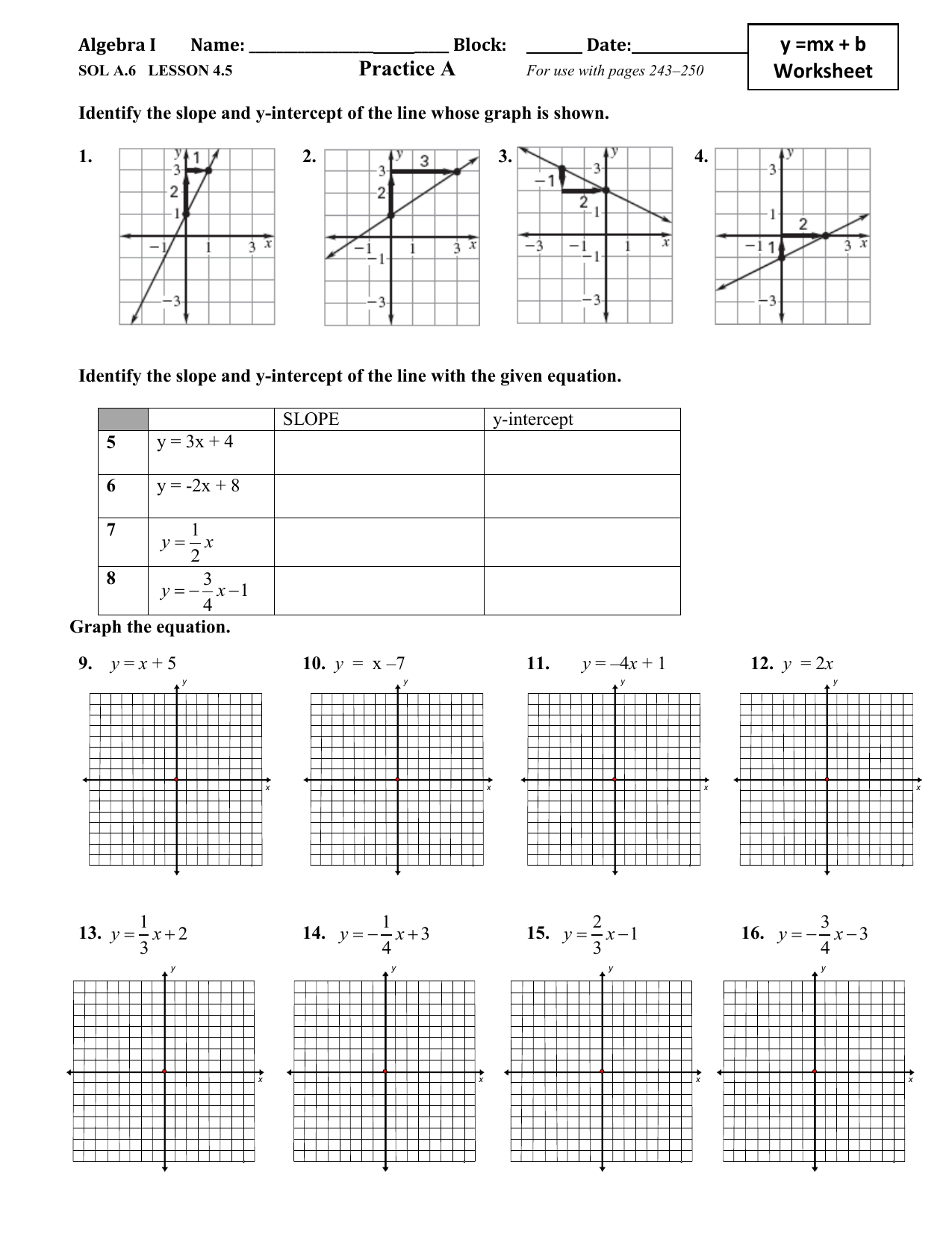
The concept of Y=Mx+B is fundamental in algebra, particularly when it comes to understanding and graphing linear equations. This Quick Guide for Students provides comprehensive answers and explanations to the commonly used Y=Mx+B Worksheet, aiding students in mastering the slope-intercept form. Let's dive into how you can work through these worksheets effectively.
Understanding the Slope-Intercept Form
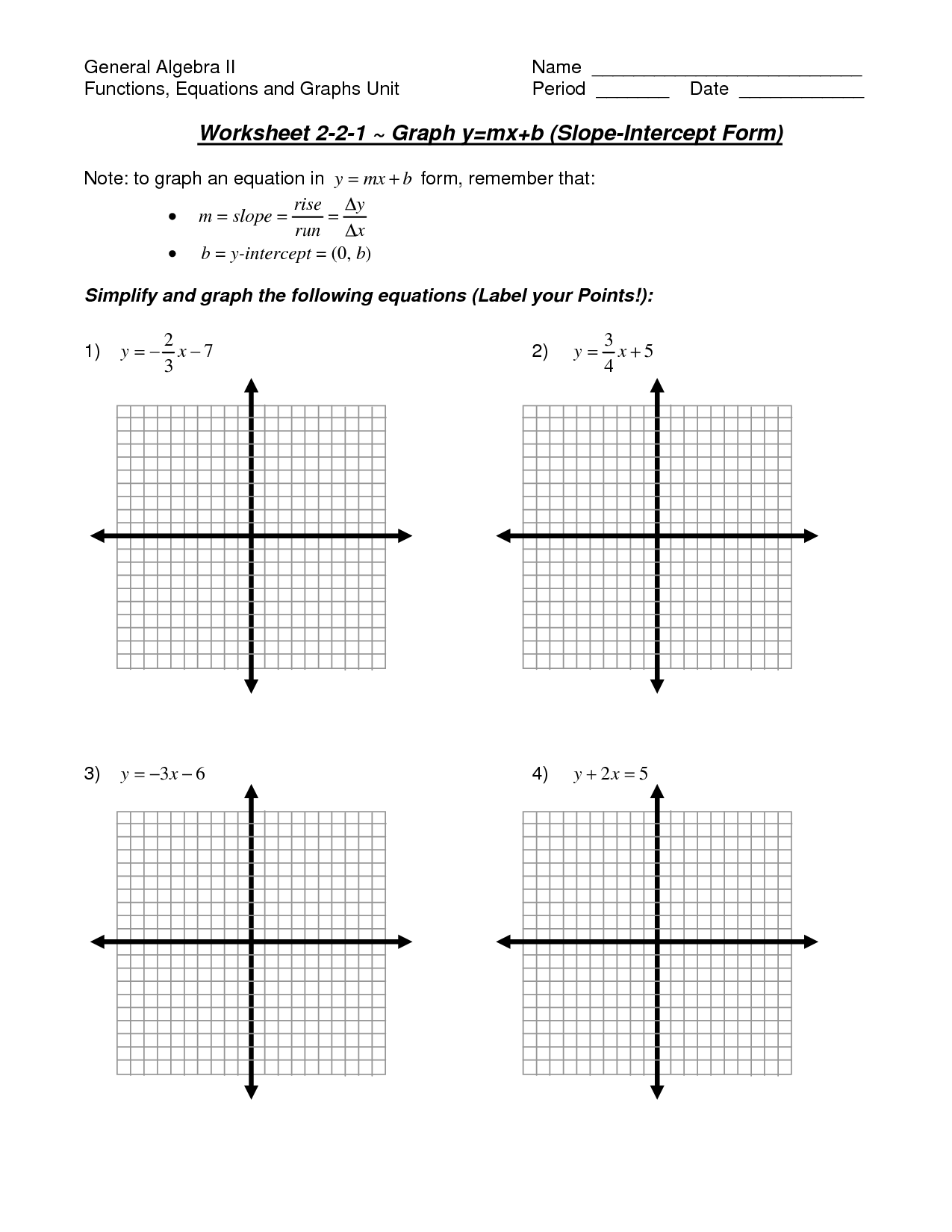
Before we delve into the worksheet answers, let’s clarify what Y=Mx+B represents:
- Y: This is your dependent variable, the vertical position on a graph.
- M: Known as the slope, it dictates how steep the line is. Positive slope means the line rises from left to right, while a negative slope indicates a decline.
- X: The independent variable, which controls the horizontal position on the graph.
- B: The y-intercept, where the line touches the y-axis when x equals zero.
How to Approach Worksheet Questions

Worksheet questions typically involve:
- Finding the slope (M) and y-intercept (B) from a given equation.
- Writing an equation in slope-intercept form given two points or a slope and a point.
- Graphing lines using the slope-intercept method.
- Solving for Y given X or vice versa.
Worksheet Example and Answers
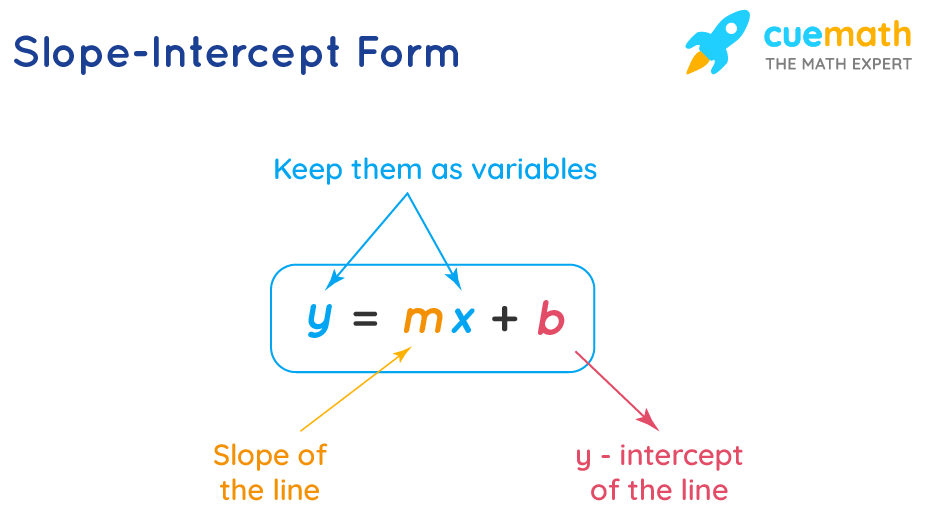
Let’s walk through some typical questions:
Question 1: Identify Slope and Y-Intercept

Given: Y = 2x + 3
Answer:
- Slope (M) = 2
- Y-intercept (B) = 3
Question 2: Write Equation in Slope-Intercept Form
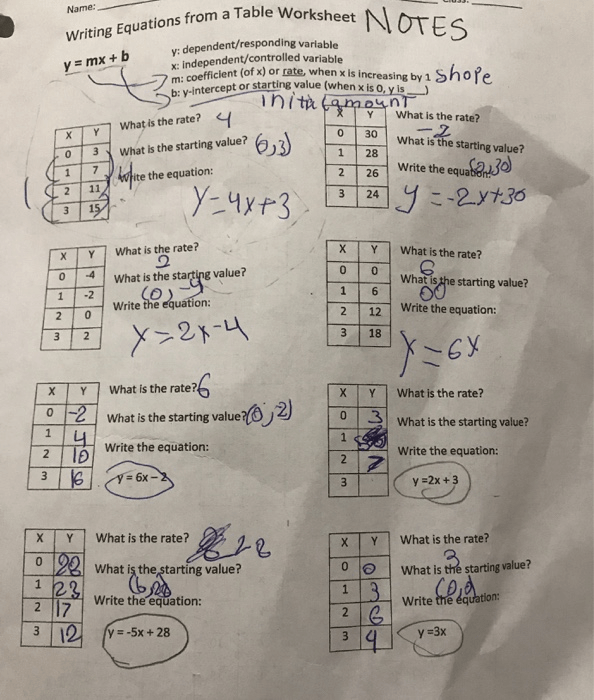
Given: Two points on the line are (1,3) and (4,9).
Solution:
- Calculate the slope (M) using the formula:
(y2 - y1) / (x2 - x1). Thus, M = (9 - 3) / (4 - 1) = 6 / 3 = 2. - Use one point and the slope to find B:
- With point (1,3): 3 = 2(1) + B. Solving for B gives B = 1.
- Therefore, the equation is Y = 2x + 1.
📝 Note: Always check your work with another point from the question to ensure accuracy.
Question 3: Graphing

Given: Y = -1/2x + 4
Solution:
- Plot the Y-intercept at (0,4).
- Use the slope to find another point: move down 1 unit (since the slope is negative) and to the right 2 units. This gives you a point at (2,3.5).
- Connect these points to graph the line.
| Point 1 | Point 2 | Slope | Y-Intercept |
|---|---|---|---|
| (0,4) | (2,3.5) | -1/2 | 4 |

Key Techniques for Mastering Y=Mx+B

To excel in working with the Y=Mx+B format, consider these tips:
- Practice Substitution: Substitute different values of X into the equation to find Y and plot points.
- Use Graphing Tools: Utilize graphing calculators or online tools to visualize your equations.
- Memorize the Slope Formula: For any two points on a line, calculate M easily.
- Understand Changes in Slope: How slope affects the line’s steepness and direction.
In wrapping up, the slope-intercept form of a linear equation is crucial for understanding how lines behave in a two-dimensional space. By mastering the interpretation of M, X, and B, students can not only solve worksheet questions but also apply this knowledge to real-world problems where linear relationships exist. Remember, practice is key; the more you work with these concepts, the more natural they will become.
What does Y=Mx+B tell us about a line?
+
This form indicates the slope (M) of the line, how steep it is, and where it intersects the y-axis (B).
How can I find the slope from two points?

+
Use the formula (y2 - y1) / (x2 - x1). Plug in the coordinates of your points and calculate.
Why is it important to know the y-intercept?

+
The y-intercept shows where the line crosses the y-axis, giving you a starting point to plot or understand the line’s position.