5 Essential Tips for Mastering Y=MX+B Worksheets
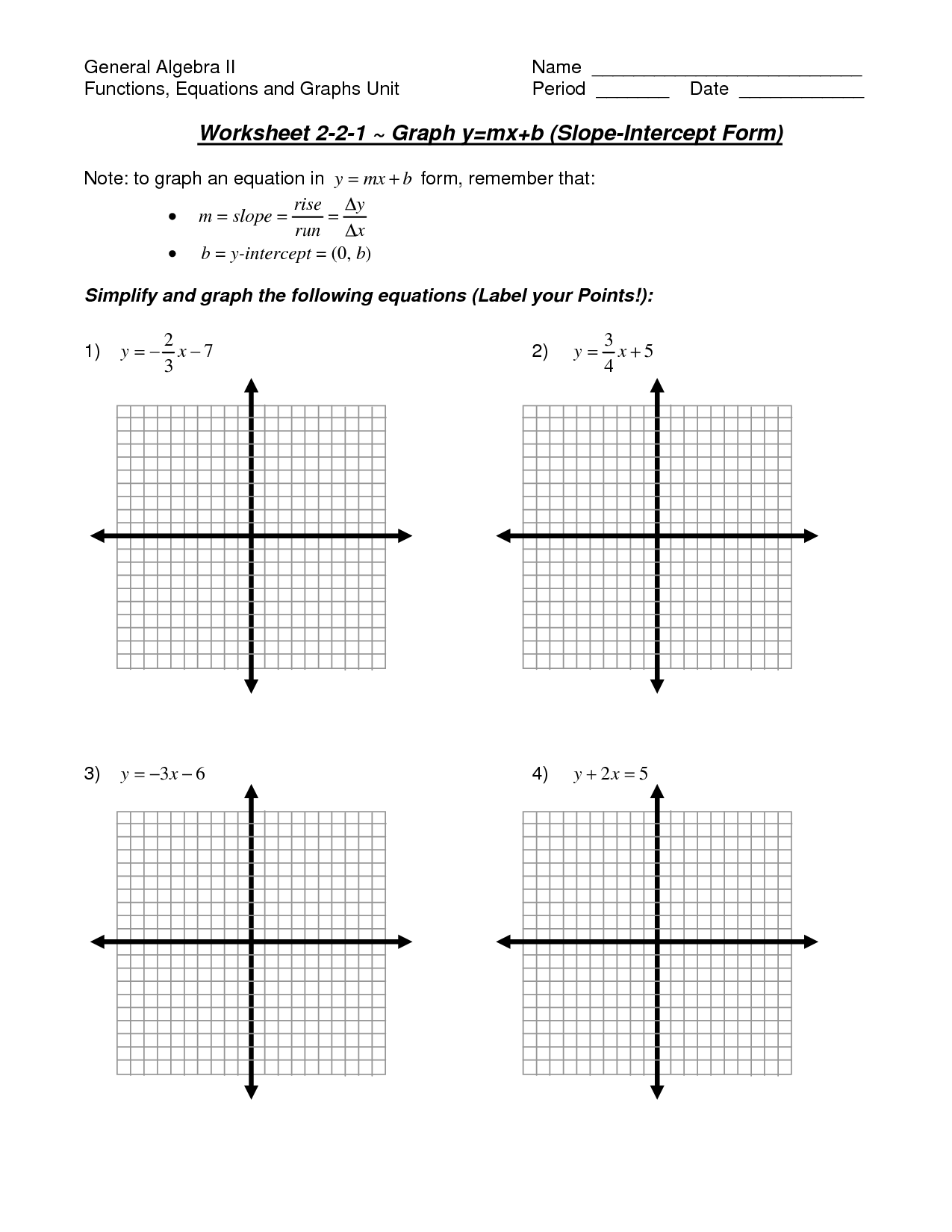
Understanding the Basics of Linear Equations

Linear equations, often represented in the form of y = mx + b, are foundational in algebra. They describe a straight line on a graph where m represents the slope (how steep the line is) and b is the y-intercept (where the line crosses the y-axis). Grasping the concept of linear equations is crucial for students and professionals alike, as it forms the basis for solving more complex mathematical problems.
Tip 1: Grasping the Concept of Slope
Understanding the slope, or gradient, is essential for any mastery of y=mx+b worksheets. Here are the steps to truly get a handle on slope:
- Visualize the concept: Slope is the rate of change between two points on a line. It tells you how much y changes for each unit increase in x.
- Understand the formula: m = (y2 - y1) / (x2 - x1). This formula calculates the slope using the coordinates of two points on the line.
- Recognize positive and negative slopes:
- A positive slope means the line goes upward from left to right.
- A negative slope means the line goes downward from left to right.
🚫 Note: Remember, a horizontal line has a slope of zero because it does not rise or fall as x changes.
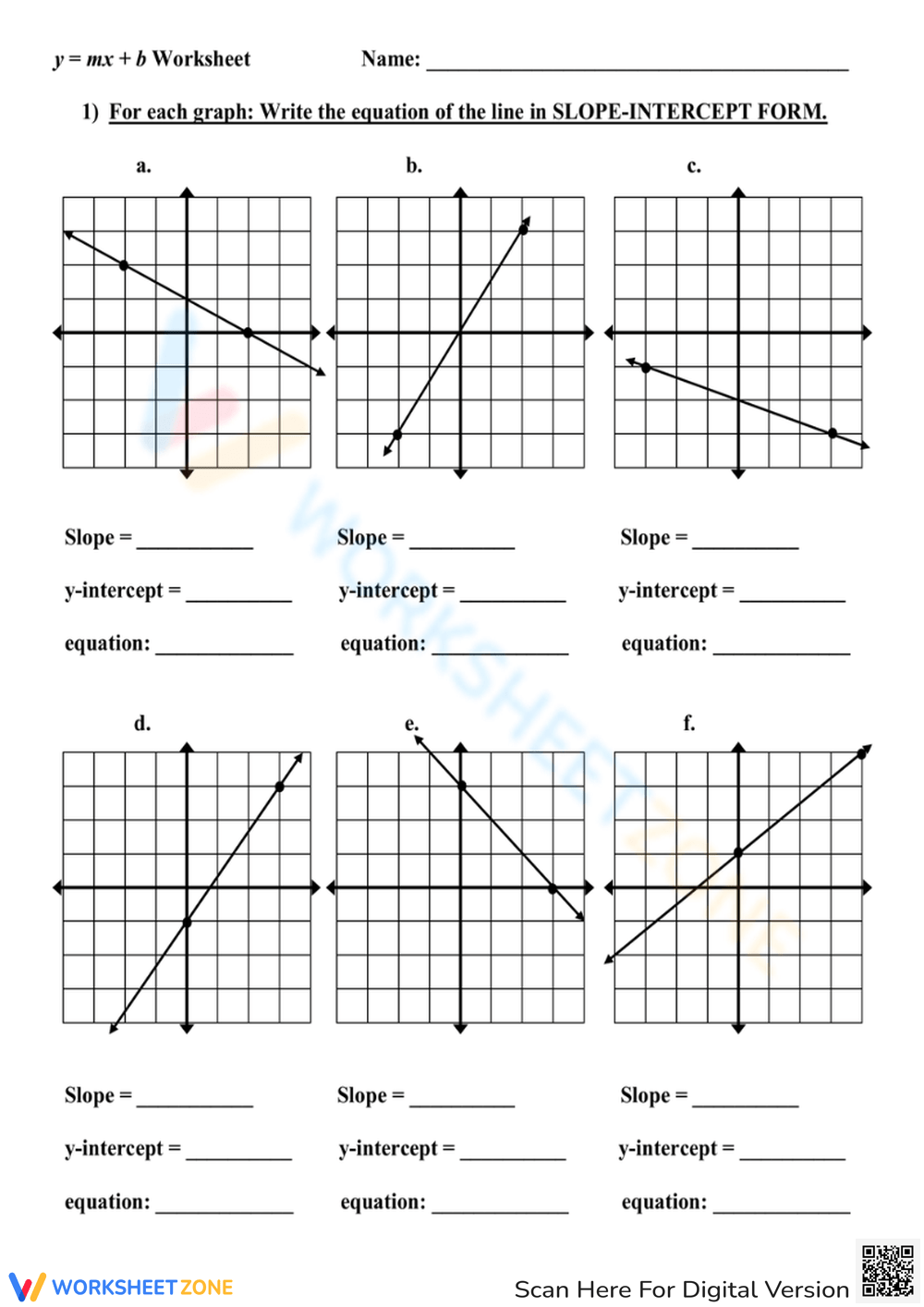
Tip 2: Identifying the Y-Intercept with Precision
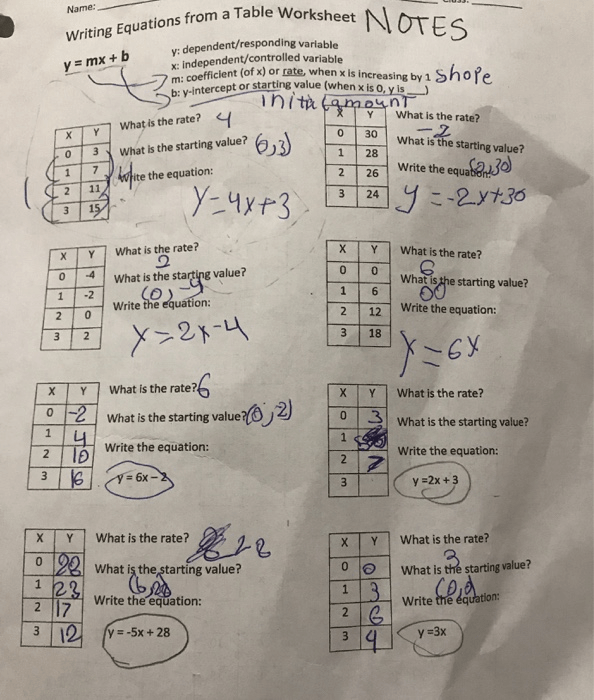
The y-intercept (b) in the equation y = mx + b is where the line hits the y-axis, and it’s crucial for graphing and understanding equations:
- Locate the Y-Intercept: It’s the point where the line crosses the y-axis, which is where x equals zero.
- Use coordinates wisely: If you’re given a graph, trace the line to the y-axis to find the y-intercept.
- Calculate from the slope: If you know the slope and one point on the line, you can find the y-intercept using algebra or graphing tools.
| Point on the Line | M (slope) | Y-Intercept (b) |
|---|---|---|
| (x1, y1) | m | b = y1 - mx1 |

Tip 3: Mastering Line Graphing

Graphing lines accurately requires an understanding of slope and y-intercept. Here’s how you can excel at it:
- Plot the y-intercept: Begin by marking the point where the line crosses the y-axis.
- Use the slope to find other points: From the y-intercept, use the rise (change in y) over run (change in x) to find another point. Repeat this process to sketch the line.
- Check your work: Ensure the line passes through the y-intercept and maintains the slope throughout.
Graphing skills not only help in visualizing linear equations but are also essential in subjects like physics and economics.
Tip 4: Solving for Equations in Context

Applying linear equations to real-world scenarios enhances your understanding of their utility:
- Identify the variables: What is the x (independent) and y (dependent) variable in the problem?
- Formulate the equation: Use the problem’s context to set up the equation with known values of slope or intercepts.
- Solve for unknowns: Use algebraic manipulation to find missing values or solve for x or y.
💡 Note: Problems involving money, distance, speed, and time often require linear equations for solution.
Tip 5: Developing Problem-Solving Skills

The ability to solve complex problems involving linear equations is a valuable skill:
- Think systematically: Break down the problem into smaller, manageable steps.
- Use visualizations: Graphing can often provide insights that algebraic solutions do not.
- Practice regularly: The more you engage with y=mx+b worksheets, the more intuitive solving problems becomes.
- Understand the real-world implications: Recognize how changes in the slope or y-intercept affect the outcome of the equation.
Mastering the nuances of y=mx+b worksheets is not just about knowing the formula but understanding its applications in various fields. The versatility of linear equations in modeling real-world phenomena underscores their importance. From finance to physics, the ability to graph and solve these equations provides a lens through which we can make predictions and analyze trends. It's clear that by immersing ourselves in this foundational concept, we equip ourselves with a mathematical tool that has both practical and theoretical value.
What does “m” represent in the equation y=mx+b?

+
In the linear equation y=mx+b, the variable “m” represents the slope of the line. It indicates how much the y-coordinate changes for a one-unit change in the x-coordinate.
How can I quickly determine the slope from a graph?

+
To quickly find the slope from a graph, you can select any two distinct points on the line and calculate the change in y (rise) divided by the change in x (run). Use the formula m = (y2 - y1) / (x2 - x1) where (x1, y1) and (x2, y2) are the coordinates of the two points.
Can linear equations help in predicting future trends?
+
Yes, linear equations can be used to predict future trends if the relationship between variables remains linear over time. By modeling historical data, you can extend the line to forecast future outcomes with the caveat that external factors are not significantly altering the trend.