5 Ways to Write Linear Equations from Tables
Introduction to Linear Equations

Linear equations are a fundamental concept in mathematics, used to describe relationships between variables. They can be represented in various forms, including tables, graphs, and equations. In this article, we will focus on writing linear equations from tables, a crucial skill in algebra and problem-solving.
Understanding the Basics of Linear Equations
A linear equation is an equation in which the highest power of the variable(s) is 1. It can be written in the form of ax + by = c, where a, b, and c are constants, and x and y are variables. Linear equations can be represented in tables, which display the input-output pairs of the equation.
Method 1: Identifying the Constant Rate of Change
One way to write a linear equation from a table is to identify the constant rate of change. This involves finding the difference in the output values for a given difference in the input values.
| x | y |
|---|---|
| 0 | 2 |
| 1 | 4 |
| 2 | 6 |
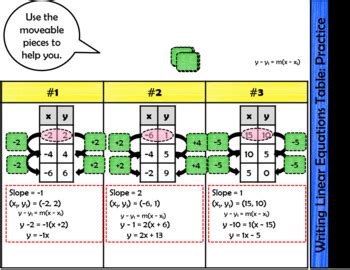
In the above table, the input values increase by 1, and the output values increase by 2. This means that the constant rate of change is 2. We can use this information to write the linear equation.
📝 Note: The constant rate of change is the ratio of the change in output to the change in input.
Using the constant rate of change, we can write the linear equation in the form of y = mx + b, where m is the constant rate of change and b is the y-intercept.
y = 2x + 2
Method 2: Using the Slope-Intercept Form

Another way to write a linear equation from a table is to use the slope-intercept form. This involves finding the slope (m) and the y-intercept (b) of the line.
| x | y |
|---|---|
| -2 | 0 |
| -1 | 2 |
| 0 | 4 |
In the above table, we can see that the line passes through the point (0, 4) and has a slope of 2. We can use this information to write the linear equation in the slope-intercept form.
y = 2x + 4
Method 3: Using the Point-Slope Form
The point-slope form is another way to write a linear equation from a table. This involves finding the slope (m) and using one of the points on the line to write the equation.
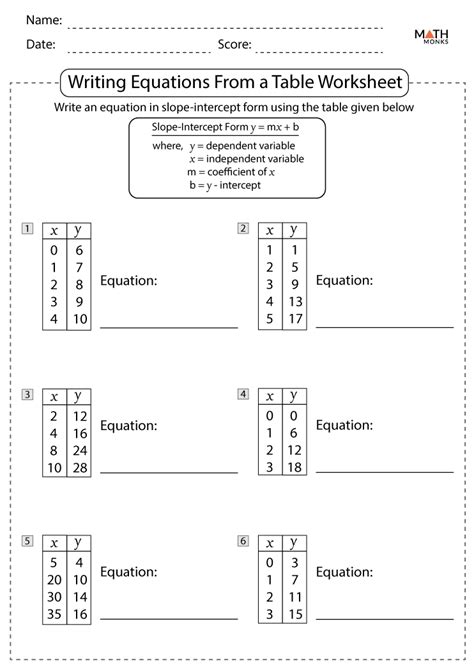
| x | y |
|---|---|
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
In the above table, we can see that the line passes through the point (1, 3) and has a slope of 2. We can use this information to write the linear equation in the point-slope form.
y - 3 = 2(x - 1)
Method 4: Using the Standard Form

The standard form is another way to write a linear equation from a table. This involves finding the coefficients of x and y and the constant term.
| x | y |
|---|---|
| 0 | 5 |
| 1 | 7 |
| 2 | 9 |
In the above table, we can see that the coefficients of x and y are 1 and -1, respectively, and the constant term is 5. We can use this information to write the linear equation in the standard form.
x - y = -5
Method 5: Using the Intercept Form

The intercept form is another way to write a linear equation from a table. This involves finding the x-intercept and the y-intercept.
| x | y |
|---|---|
| -3 | 0 |
| 0 | 2 |
| 3 | 4 |
In the above table, we can see that the x-intercept is -3 and the y-intercept is 2. We can use this information to write the linear equation in the intercept form.
x/(-3) + y/2 = 1
In conclusion, writing linear equations from tables is an essential skill in mathematics. By using the five methods outlined above, you can easily write linear equations from tables. Remember to always identify the constant rate of change, slope, and intercepts to write the equation in the desired form.
What is the difference between the slope-intercept form and the point-slope form?
+
The slope-intercept form is used to write a linear equation in the form y = mx + b, where m is the slope and b is the y-intercept. The point-slope form is used to write a linear equation in the form y - y1 = m(x - x1), where m is the slope and (x1, y1) is a point on the line.
How do I find the x-intercept of a linear equation?

+
The x-intercept is the point where the line crosses the x-axis. To find the x-intercept, set y = 0 and solve for x.
What is the constant rate of change?

+
The constant rate of change is the ratio of the change in output to the change in input. It is used to write linear equations in the form y = mx + b.
Related Terms:
- function table linear answer key
- linear equations worksheet pdf kuta
- writing linear equations worksheet kuta
- linear function tables worksheet pdf
- writing linear equations pdf
- writing equations from tables pdf