Master Writing Inequalities with Our Fun Worksheet

Writing inequalities is a fundamental skill in mathematics, often crucial for solving real-world problems and decision-making processes. Whether you're a student in middle school, high school, or even an adult revisiting math concepts, understanding how to formulate and solve inequalities can be immensely beneficial. In this comprehensive blog post, we'll dive into how you can master writing inequalities with the help of our engaging worksheet. This guide will walk you through the basics, provide practical examples, and ensure you're well-equipped to tackle any inequality problem you encounter.
The Basics of Writing Inequalities

Before we jump into the worksheet, let’s review some fundamental principles about inequalities:
- Inequality Symbols: The most common inequality symbols you'll encounter include:
- > (greater than)
- < (less than)
- ≥ (greater than or equal to)
- ≤ (less than or equal to)
- ≠ (not equal to)
- Real-world Interpretation: Inequalities describe situations where one value is larger or smaller than another, but not necessarily equal.
- Key Rules:
- Adding or subtracting the same number from both sides of an inequality does not change the truth of the inequality.
- Multiplying or dividing both sides by a positive number does not change the inequality direction.
- Multiplying or dividing by a negative number reverses the inequality direction.

Understanding Our Fun Worksheet

Our worksheet is designed to make learning about inequalities both fun and educational. Here’s what you’ll find:
- Visual Representations: Diagrams to help you visualize different inequality scenarios.
- Practice Problems: A range of problems from easy to more challenging, allowing you to build your skills gradually.
- Hints and Tricks: Tips to help you solve inequalities quicker or recognize common pitfalls.
Step-by-Step Guide to Writing Inequalities

To get you started, here’s a step-by-step guide on how to use our worksheet effectively:
1. Familiarize Yourself with Symbols

Begin by reviewing the inequality symbols and their meanings. Here is a quick reminder:
| Symbol | Meaning |
|---|---|
| > | Greater than |
| < | Less than |
| ≥ | Greater than or equal to |
| ≤ | Less than or equal to |
| ≠ | Not equal to |

2. Solve Simple Inequalities

Start with basic inequalities like:
- 5x < 10
- y - 3 ≥ 7
Remember to:
- Isolate the variable on one side.
- Apply the rules to maintain the inequality.
- Check your work.
🔍 Note: Always double-check your answers to ensure you haven't accidentally flipped the inequality sign when multiplying or dividing by a negative number.
3. Compound Inequalities

Progress to compound inequalities, which involve two conditions. For instance:
- 0 < x < 10
- -1 ≤ y ≤ 5
Here, you'll need to solve both sides of the inequality simultaneously.
4. Real-World Applications

Our worksheet includes scenarios where inequalities arise naturally:
- Budgeting: You have $100 to spend, and a new item costs $25. Write an inequality to represent this situation.
- Physics: Represent the maximum force a spring can handle before breaking.
- Manufacturing: A factory can produce no more than 2000 units a day.
This will help you understand the practical use of inequalities.
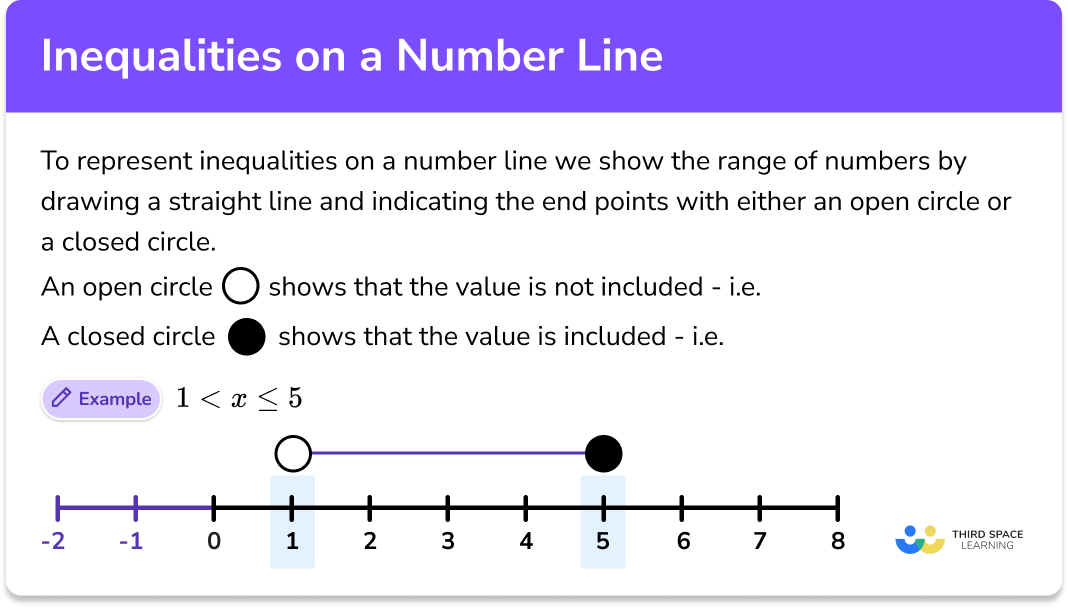
5. Graphing Inequalities on a Number Line

Graphing is an excellent way to visualize where the solutions to an inequality lie. Our worksheet includes exercises to plot inequalities on a number line:
- Draw an open circle for > or < and a closed circle for ≥ or ≤.
- Extend lines to show the range of solutions.

6. Advanced Topics

Once you’re comfortable with the basics, delve into more complex inequalities:
- Absolute Value Inequalities: Learn how to handle absolute values like |x - 3| < 5.
- Quadratic Inequalities: Solve inequalities involving quadratic expressions like x2 + 2x ≥ 0.
- Systems of Inequalities: Explore how multiple inequalities interact to find solutions that satisfy all conditions.
🌐 Note: For more advanced topics, online resources and textbooks can provide additional depth and practice.
Mastery Through Practice
Mastery comes from repeated exposure and practice:
- Regularly Review: Keep revisiting basic concepts to reinforce your understanding.
- Explore Different Contexts: Try solving inequalities in various scenarios to build your problem-solving toolkit.
- Time Yourself: Set time limits for solving problems to improve your speed and accuracy.
By mastering these steps with our worksheet, you'll not only understand inequalities but also be able to apply them confidently.
Your Journey Forward

As you work through our worksheet, remember that every mistake is a learning opportunity. Mathematics is about problem-solving, and inequalities offer a unique lens through which to view these problems. Here are some final tips to help you on your journey:
- Visualize: Always try to picture what the inequality is describing.
- Connect: Link what you're learning to real-world problems for better retention.
- Practice: Consistent practice is key. The more you work with inequalities, the more intuitive they become.
In the end, the ability to write and solve inequalities will enhance not just your mathematical prowess but also your decision-making skills in everyday life, from budgeting to time management. Embrace the challenge, enjoy the process, and soon you'll see that inequalities are not just about numbers but about navigating life's complexities with clarity.
What is the difference between “less than” and “less than or equal to” symbols?

+
The “less than” symbol (<) indicates that the value on the left is strictly smaller than the one on the right, excluding the possibility of equality. In contrast, “less than or equal to” (≤) means that the value on the left can be either smaller or equal to the one on the right. This small difference can significantly affect the solutions to your inequalities.
How can I tell if I need to reverse the inequality sign?
+
You need to reverse the inequality sign when you multiply or divide both sides of the inequality by a negative number. For example, if you’re solving -2x < 4, dividing both sides by -2 gives x > -2, not x < -2.
Why are inequalities useful in real life?

+
Inequalities are useful because they help us define and understand limits and constraints. They are essential in:
- Finance, for budget planning and cost projections
- Engineering, to set tolerances and specifications
- Physics, to determine acceptable ranges of variables like force or speed
- Daily life, for tasks such as time management and scheduling.