5 Easy Steps to Master Graph Equation Writing

In the dynamic world of mathematics, graph equations play a pivotal role in expressing data visually, making abstract concepts tangible. Whether you're delving into algebra, calculus, or advanced statistical analysis, learning to write graph equations is an invaluable skill. This guide will walk you through 5 easy steps to master graph equation writing, turning complex mathematical expressions into clear, interpretable graphs.
Understanding Basic Concepts
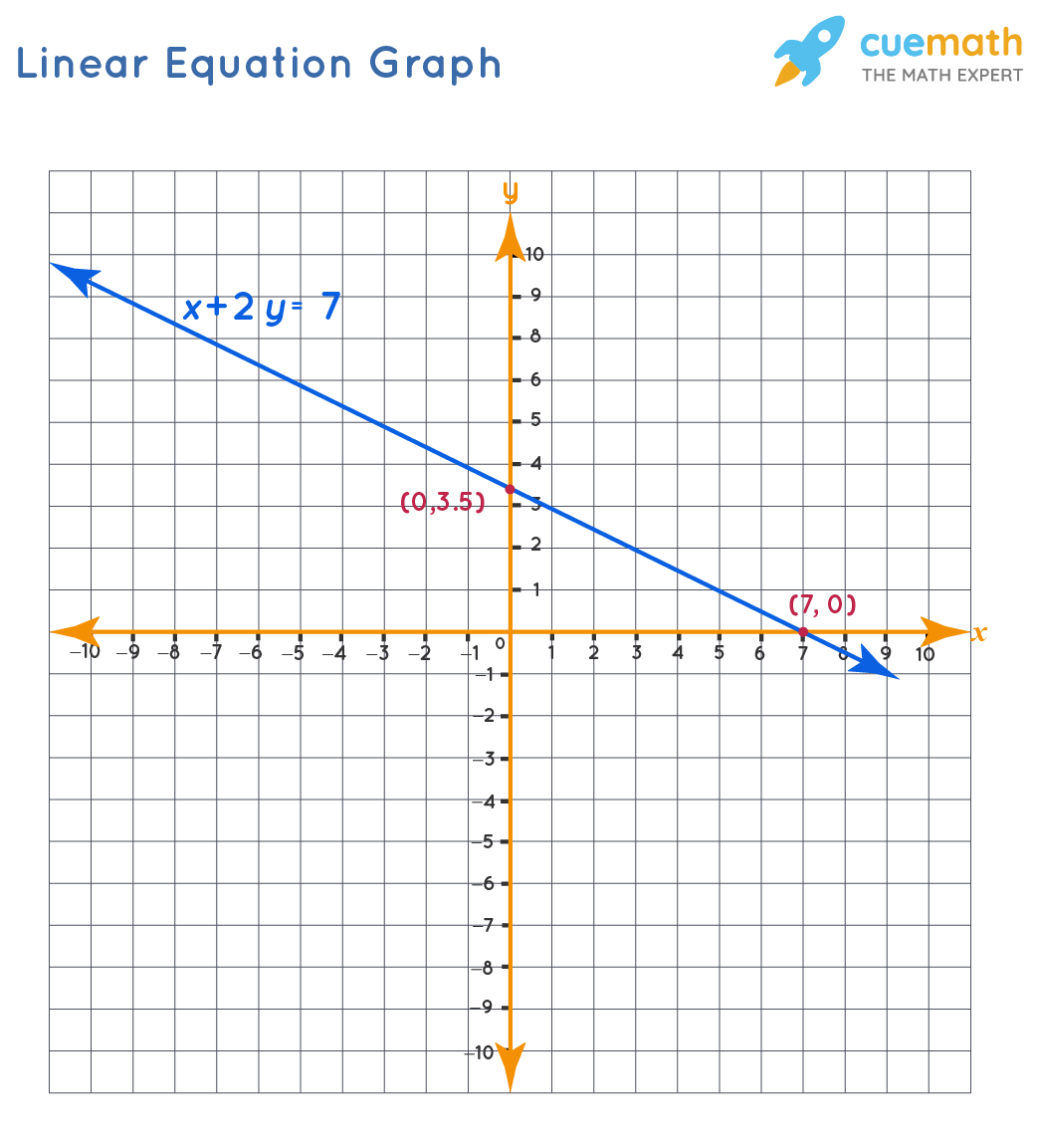
Before diving into the art of graph equation writing, it’s imperative to grasp the fundamentals:
- Variables and Constants: In an equation, variables are the unknowns (e.g., x, y), while constants are fixed values.
- Functions: A function is a rule that assigns each element in a set of inputs to exactly one output.
- Coordinates: Points on a graph defined by pairs of numbers, usually written as (x, y).
🔔 Note: Ensuring a solid understanding of these basic concepts will pave the way for smoother graph equation writing.
Identifying Variables

Graph equations usually involve at least two variables:
- The independent variable (x-axis), which you control.
- The dependent variable (y-axis), which changes based on the independent variable.
Identifying these variables is crucial as it sets the stage for the type of graph you’ll be plotting:
| Equation Example | Independent Variable (x) | Dependent Variable (y) |
|---|---|---|
| y = 2x + 1 | x | y |
| y = x^2 | x | y |

Setting up the Coordinate System
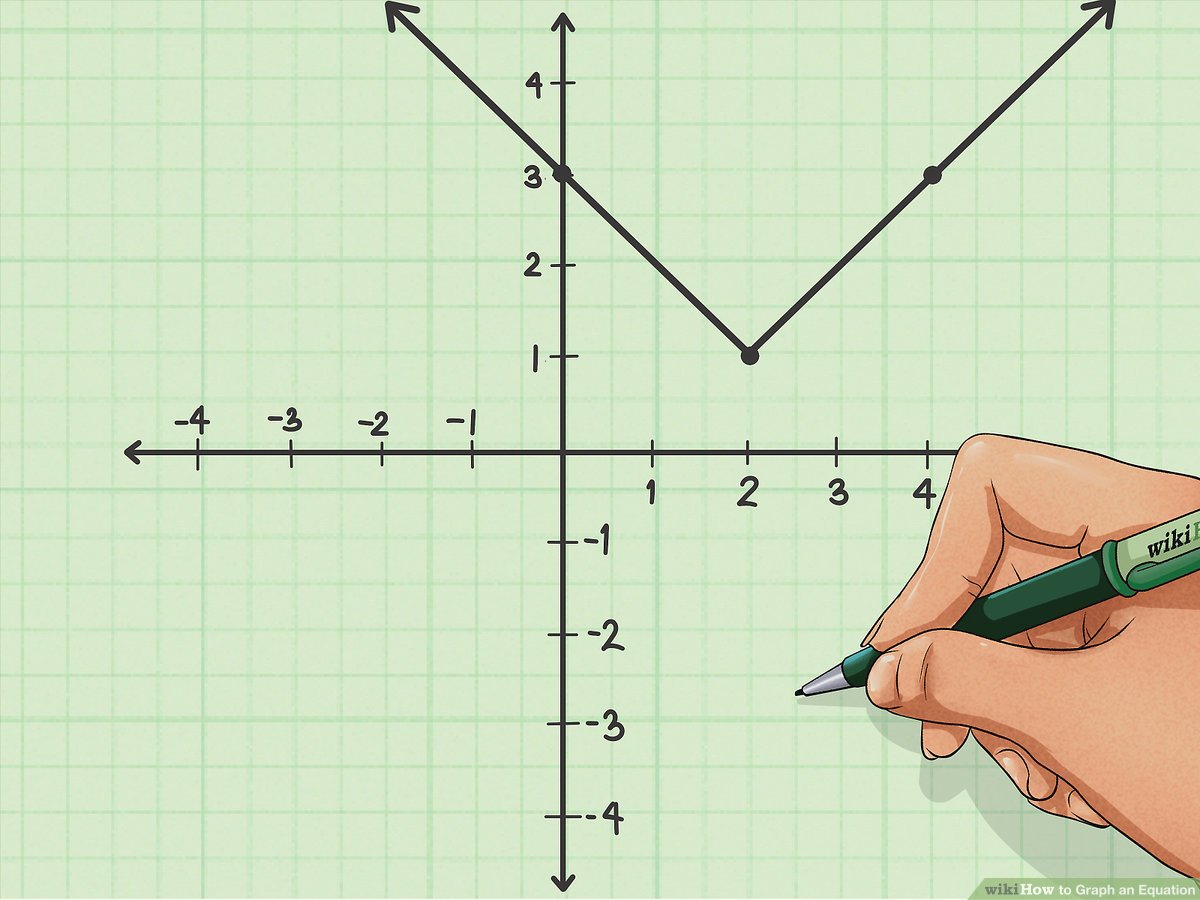
Once you’ve identified your variables, setting up the coordinate system is the next step:
- Choose appropriate scales for each axis based on your data.
- Draw the axes, ensuring the origin (0,0) is clearly marked.
- Label the axes with variable names and units if applicable.
The choice of scales will influence how clearly the graph will represent your data. Here, the consideration is to make the visual representation as intuitive as possible for analysis.
Plotting Points

With your coordinate system ready, you can now plot points:
- Select a range of values for your independent variable (x).
- Calculate corresponding y-values for each x using your equation.
- Plot these points on your graph, marking them distinctly.
🔍 Note: The more points you plot, the smoother your curve will be, enhancing the accuracy of your graph equation.
Connecting the Dots

After plotting points, you’ll proceed to connect them to form the curve or line:
- Determine the type of graph you need: line, curve, scatter plot, etc.
- Connect the points smoothly, ensuring continuity and accuracy in representation.
- Consider the shape of the graph to understand the behavior of your equation better.
Remember, the type of graph you choose should reflect the nature of your data and the equation:
| Graph Type | Best for Equations… |
|---|---|
| Line Graph | Linear equations (y = mx + c) |
| Curve Plot | Polynomial, exponential, or logarithmic equations |
| Scatter Plot | Non-linear or no specific equation; to observe patterns |
💡 Note: While these steps outline a straightforward path to graph equation writing, creativity and understanding of the underlying data will refine your skills further.
In summary, the art of writing graph equations is not just about plotting lines on a paper. It's about understanding the mathematical relationships within the data, translating those into visual representations, and interpreting what those visuals mean. Each step, from understanding the basic concepts to connecting the dots, is crucial in crafting a graph that accurately represents the equation at hand. Through practice and a keen eye for detail, you can master this skill, unlocking insights from complex data sets with ease.
Why is it important to identify variables before plotting?
+
Identifying variables is crucial because it determines how you will set up your graph and interpret the data. It establishes which variable is dependent on the other, helping you to plot the correct relationship.
What should I do if my equation produces a very steep or flat curve?
+
If your equation results in a very steep or flat curve, consider adjusting your scale on the axes. A smaller scale on the y-axis for steep curves or a larger scale on the x-axis for flat curves can make the graph more readable.
How can I make my graph equation writing more accurate?

+
To improve accuracy, plot more points, especially around critical points where the curve changes direction. Use mathematical tools or software to check your work, and ensure you’re using the correct scale and understanding of the equation’s behavior.