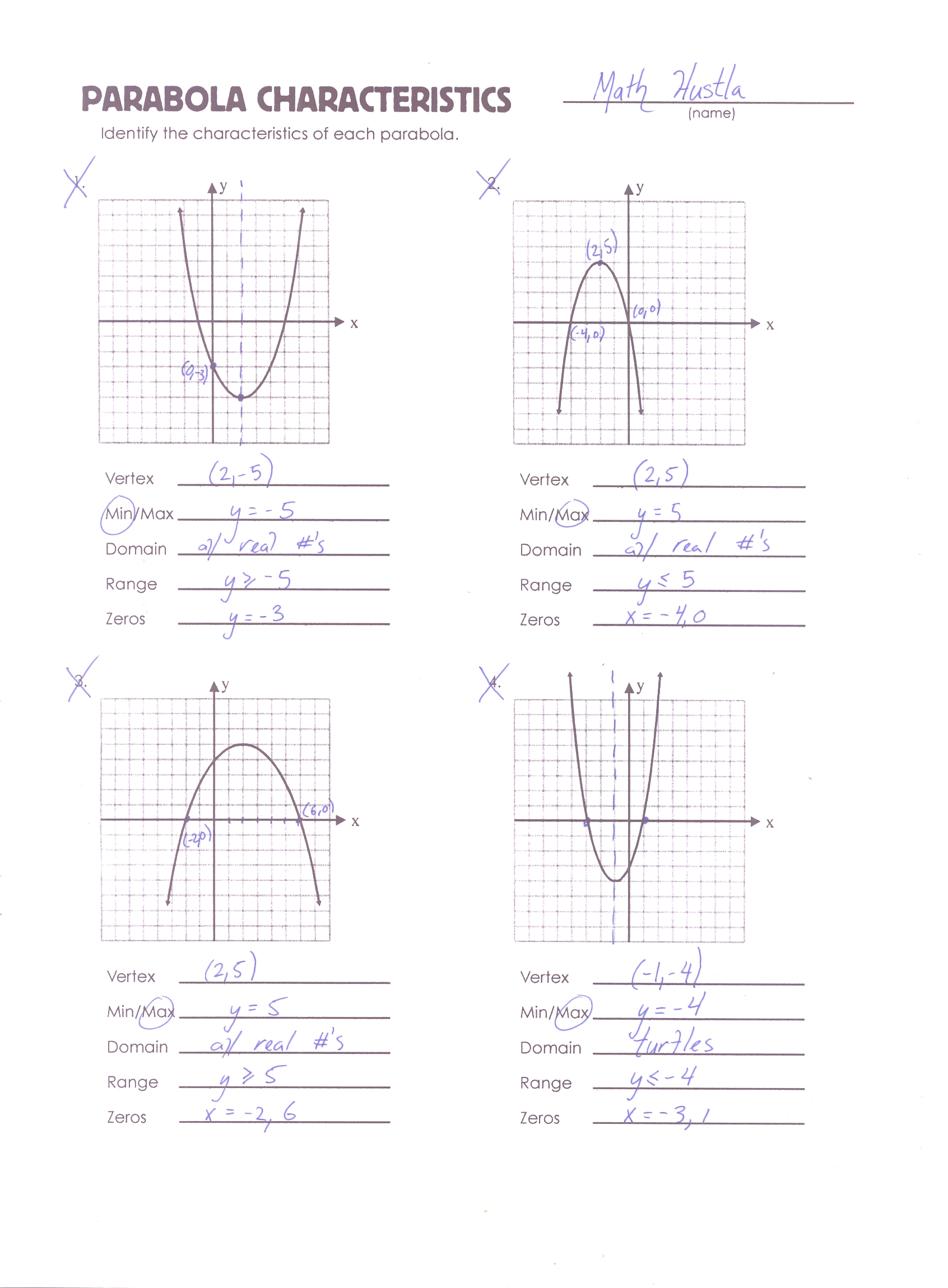
Parabola Worksheets: Master the Curve with Ease

The world of mathematics is filled with intriguing curves, and the parabola stands out for its elegance and application in various fields from engineering to physics. Mastering parabolas can be a gateway to understanding more complex mathematical principles and their practical applications. This extensive guide will provide you with the essential worksheets and insights to master the parabola with ease.
Understanding Parabolas

A parabola is a U-shaped curve that is symmetrical. It arises from the quadratic equation in its general form:
y = ax2 + bx + c
- a determines the parabola's orientation: if a > 0, the parabola opens upwards; if a < 0, it opens downwards.
- b affects the position and steepness of the parabola.
- c shifts the parabola vertically.

Parabola Worksheets: Your Learning Journey
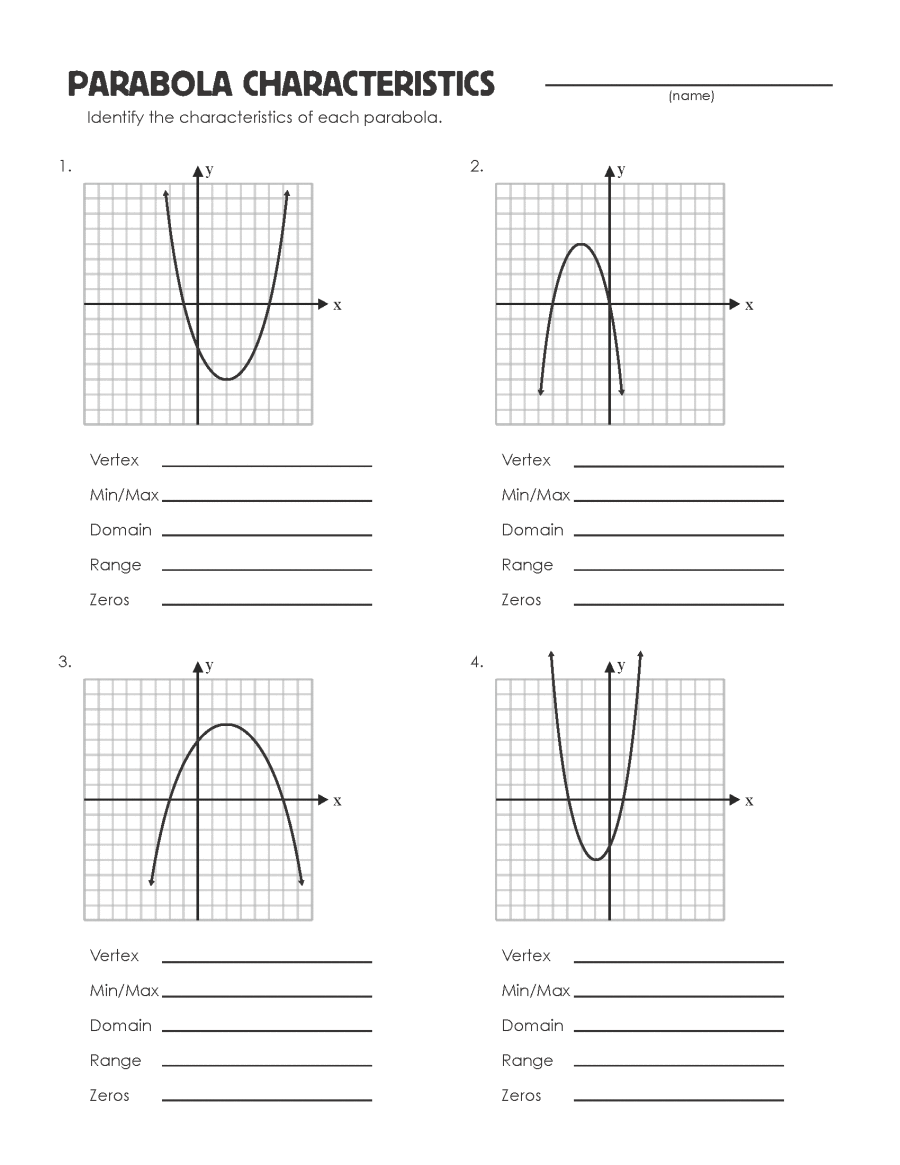
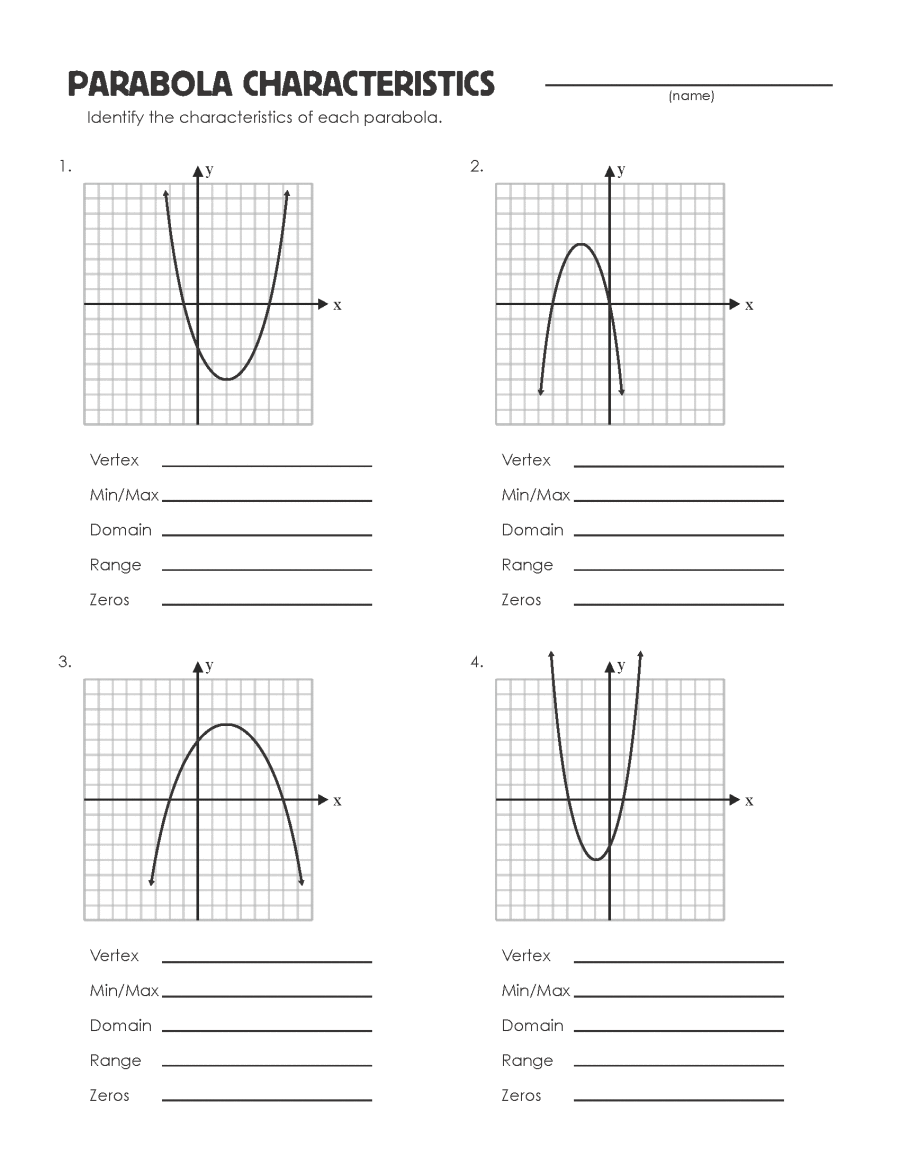
Here are some worksheets tailored to help you grasp parabolas effectively:
Worksheet 1: Graphing Parabolas

This worksheet will guide you through:
- Plotting parabolas from given equations.
- Identifying key points like the vertex and focus.
- Determining the direction of the parabola based on ‘a’.
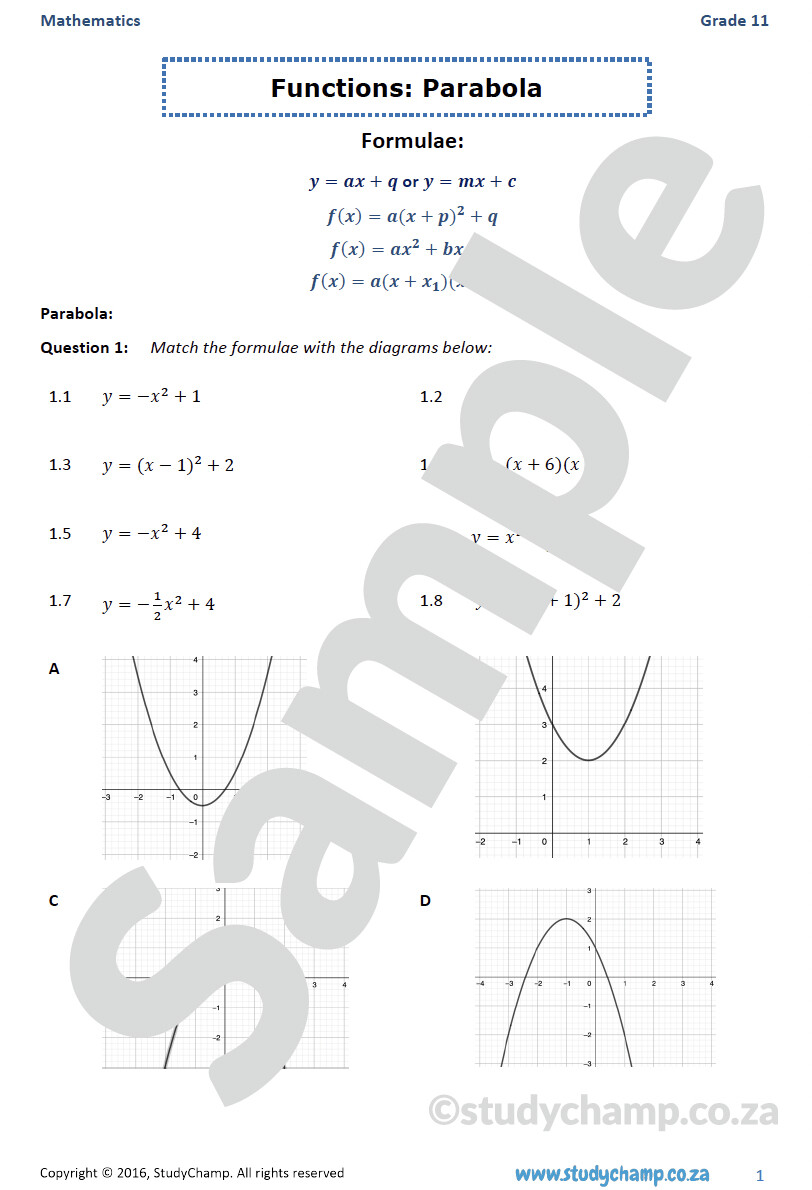
Worksheet 2: Vertex Form
The vertex form of a parabola equation is:
y = a(x - h)2 + k
- Work on converting standard form to vertex form.
- Find the vertex directly from the equation.
| Standard Form | Vertex Form | Vertex |
|---|---|---|
| y = x2 + 6x + 8 | y = (x + 3)2 - 1 | (-3, -1) |
📝 Note: The vertex form is particularly useful when you need to quickly find the vertex of the parabola without graphing.
Worksheet 3: Real-World Applications

This worksheet focuses on:
- Applying parabola properties to solve projectile motion problems.
- Calculating focal distances for reflecting surfaces like satellite dishes.
Worksheet 4: Axis of Symmetry

Every parabola has an axis of symmetry, which is a vertical line that divides the parabola into two mirror images:
- Identify the axis of symmetry using the equation.
- Verify this by plotting the parabola and reflecting points.
Worksheet 5: Focus and Directrix
The focus and directrix are critical elements of parabolas:
- Calculate the distance between the focus and vertex (p).
- Explore how changing p affects the shape and spread of the parabola.
Mastering Parabolas: Tips and Tricks
Here are some strategies to excel in working with parabolas:
- Memorize the standard forms – Knowing the standard and vertex forms by heart will speed up your problem-solving.
- Understand the symmetry – The symmetry of parabolas simplifies solving equations and graphing.
- Practice with a variety of equations – Work through different types of quadratic equations to understand how slight changes affect the parabola's shape.
- Use tools like graphing calculators – They can provide a visual understanding of what happens when you change coefficients.
Summary

The journey through parabolas not only enhances your understanding of algebra but also sets a foundation for more advanced mathematics. By diligently working through the provided worksheets, you’ll become adept at:
- Recognizing and graphing parabolas from their equations.
- Manipulating equations to find vertices and axes of symmetry.
- Applying parabolic principles to real-world scenarios.
Remember, mastering parabolas isn’t just about solving equations; it’s about appreciating the beauty and utility of this curve in both theoretical and practical contexts.
Why is the parabola important in mathematics?

+
Parabolas are crucial in mathematics because they model numerous physical phenomena, including projectile motion, reflectors in optics, and even certain financial models.
How can I find the focus and directrix of a parabola?

+
The distance ‘p’ from the vertex to the focus or directrix can be calculated using the formula p = 1/(4a) where a is the coefficient of x2 in the standard form of the parabola.
Can parabolas open horizontally?

+
Yes, parabolas can open horizontally when the equation includes x as the squared term and y as the linear term.
What are some common mistakes to avoid when working with parabolas?

+
Mistakes to avoid include mixing up the ‘a’ coefficient with the sign (negative vs. positive), incorrectly identifying the vertex, and not accounting for the shift caused by ‘h’ and ‘k’ in the vertex form.