5 Worksheets to Master Equivalent Fractions Easily

Mastering equivalent fractions can be a daunting task for many students. However, with the right tools and techniques, understanding and manipulating fractions becomes much easier. This blog post outlines five interactive worksheets designed to guide students of all levels through the intricacies of equivalent fractions. Whether you're a teacher, a parent, or a student, these resources will offer practical exercises to solidify your grasp on fractions.
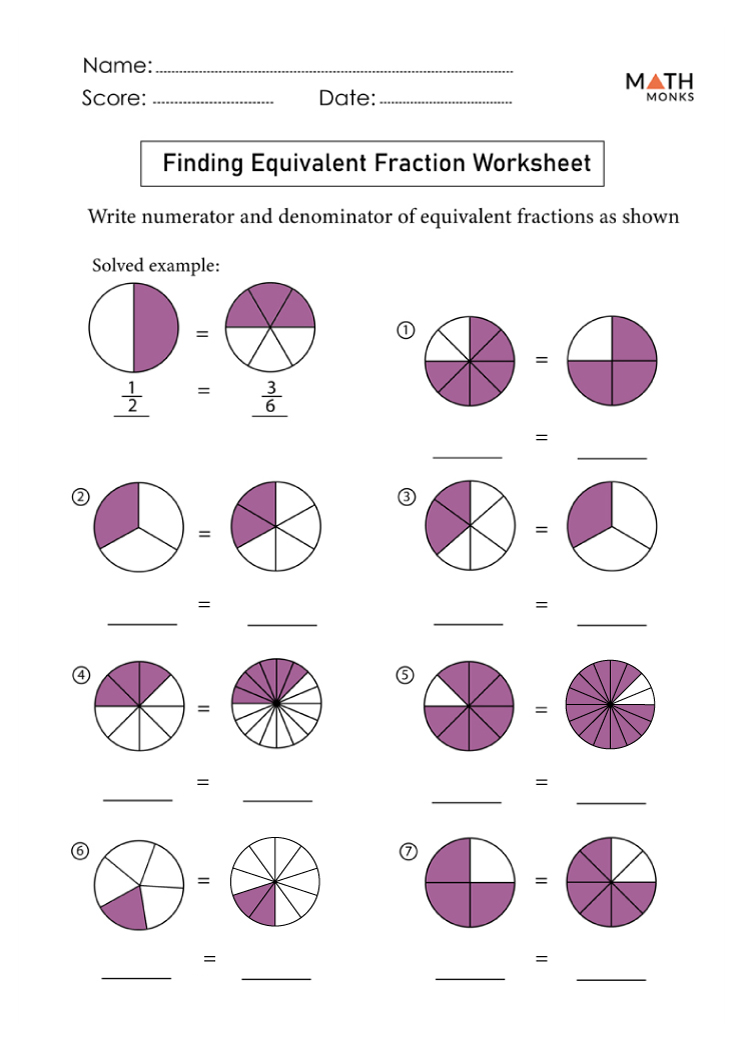
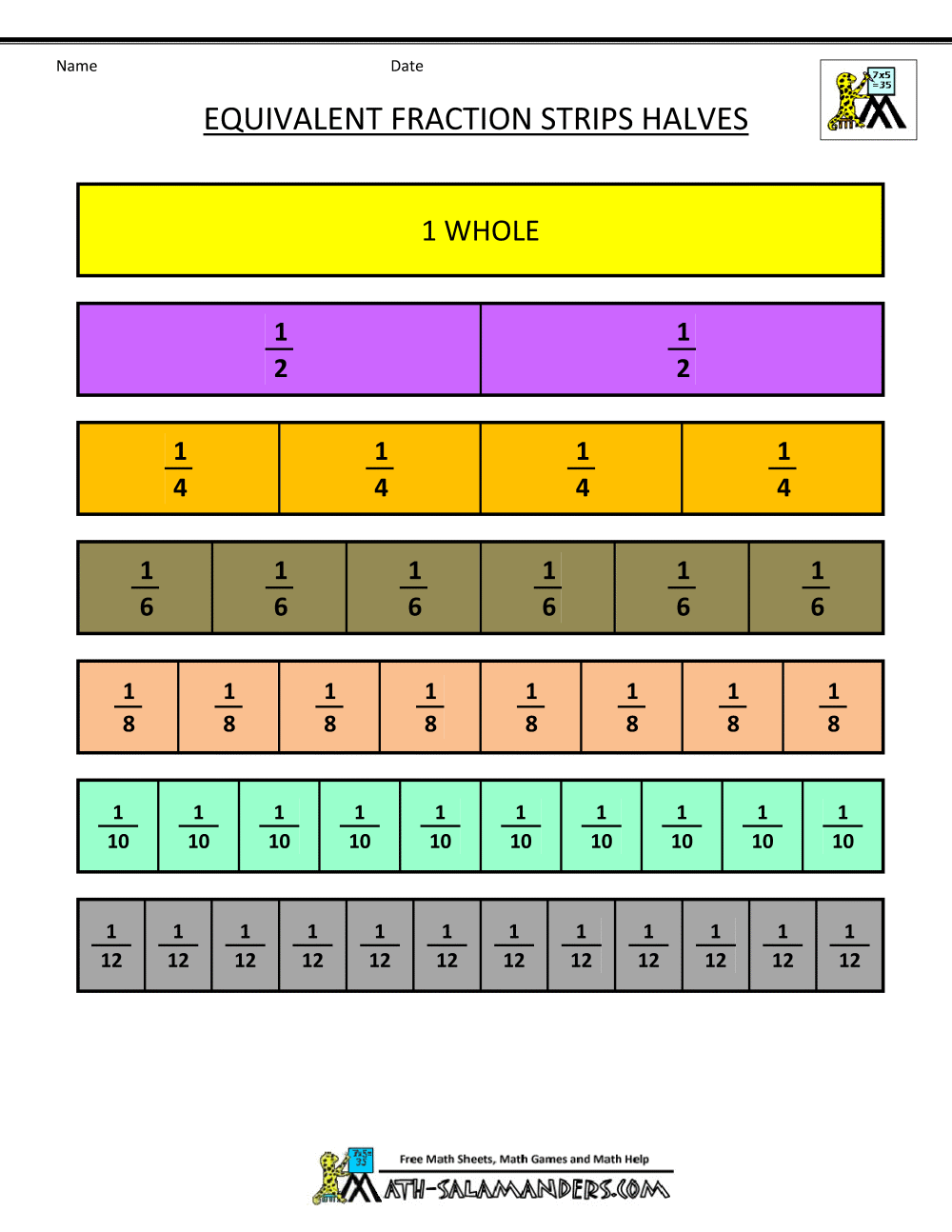
Worksheet 1: Introduction to Equivalent Fractions

The first step in understanding equivalent fractions is to recognize that different fractions can represent the same portion of a whole. Here are some exercises to help:
- Write five fractions that are equivalent to 1⁄2.
- Using visual models, draw circles to show equivalent fractions for 1⁄3, 2⁄6, 3⁄9, 4⁄12.
- Fill in the blanks: 1⁄4 = __ / 8
🔍 Note: Fractions are equivalent when they represent the same value, regardless of their appearance.
Worksheet 2: Simplifying Fractions

Before comparing or finding equivalent fractions, it’s useful to know how to simplify them. This worksheet focuses on:
| Fraction | Simplified Form |
|---|---|
| 16⁄20 | 4⁄5 |
| 28⁄42 | 2⁄3 |
| 10⁄15 | 2⁄3 |
- Find the greatest common divisor (GCD) for each pair of numerator and denominator.
- Divide both by the GCD to get the simplest form.
- Identify fractions that are already in their simplest form.
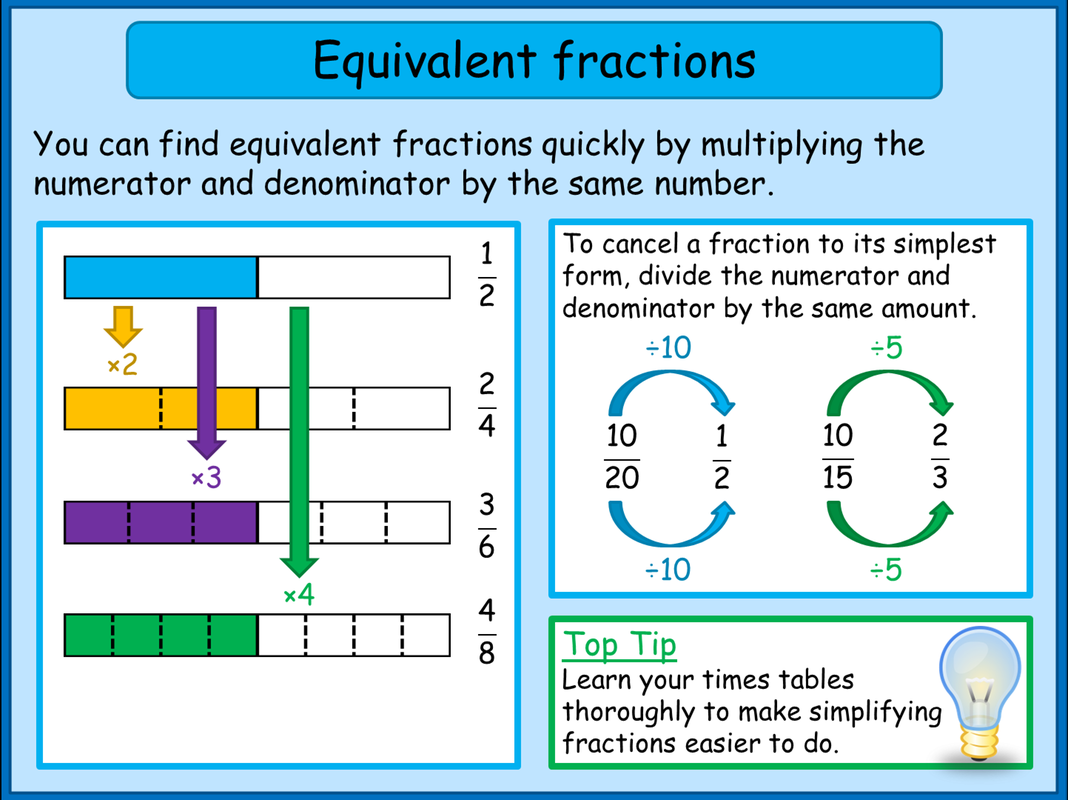
Worksheet 3: Generating Equivalent Fractions

This worksheet introduces techniques to create equivalent fractions through multiplication and division:
- Multiply both the numerator and denominator by the same number to generate equivalent fractions.
- Choose a number and divide both parts of a fraction to find another equivalent fraction.
- Practice converting fractions into different forms for quick identification of equivalency.
🔢 Note: Always ensure that both the numerator and denominator are multiplied or divided by the same number.
Worksheet 4: Comparing Fractions
Comparing fractions isn’t just about knowing their decimal forms; it’s about understanding their relative sizes:
- Use cross-multiplication to compare unlike fractions.
- Convert fractions to like denominators to compare directly.
- Identify when two fractions are equal or equivalent through numerical and visual methods.
Worksheet 5: Real-World Applications


Putting theory into practice helps solidify understanding. Here, students will:
- Solve word problems involving fraction division to find real-world equivalent fractions.
- Calculate parts of a whole or compare different quantities using fractions.
- Use fractions in recipes, measurements, and other practical applications.
By working through these worksheets, students will not only gain confidence in handling fractions but also develop a deeper understanding of their intrinsic nature. Equivalent fractions are everywhere in mathematics, from basic arithmetic to complex algebra, making this skill indispensable for any student of math.
Why is simplifying fractions important for understanding equivalent fractions?

+
Simplifying fractions helps to reveal when two fractions are equivalent, even if they look different. It reduces complexity, making it easier to compare and understand fractions at their core.
How can visual models aid in learning equivalent fractions?

+
Visual models provide a concrete representation of abstract concepts, allowing students to “see” the equality of fractions through direct comparison, which can be particularly effective for visual learners.
What is the significance of real-world applications in learning fractions?
+
Real-world applications make the abstract math of fractions tangible, showing students how these numbers are used in daily life, which reinforces the concept through practical understanding.