5 Tips for Mastering Rational Exponents Worksheets

Mastering rational exponents is an essential skill for students tackling advanced mathematics, particularly in algebra, pre-calculus, and beyond. This mathematical concept can unlock a deeper understanding of functions, equations, and problem-solving in various fields of study. Here, we'll explore five critical tips to help you become proficient in handling rational exponents through worksheets, which are the best tools for practice and mastery.
Tip 1: Understand the Basics

Before you dive into worksheets, make sure you grasp the fundamental concepts:
- Definition: Rational exponents can be written as fractions where the numerator is the power and the denominator is the root. For example, (a^{\frac{m}{n}}) means taking the nth root of ‘a’ raised to the mth power.
- Basic Properties: Familiarize yourself with how rational exponents interact with standard arithmetic operations.
🚨 Note: Rational exponents are not just about memorizing formulas but understanding their implications.
Tip 2: Practice Simplification
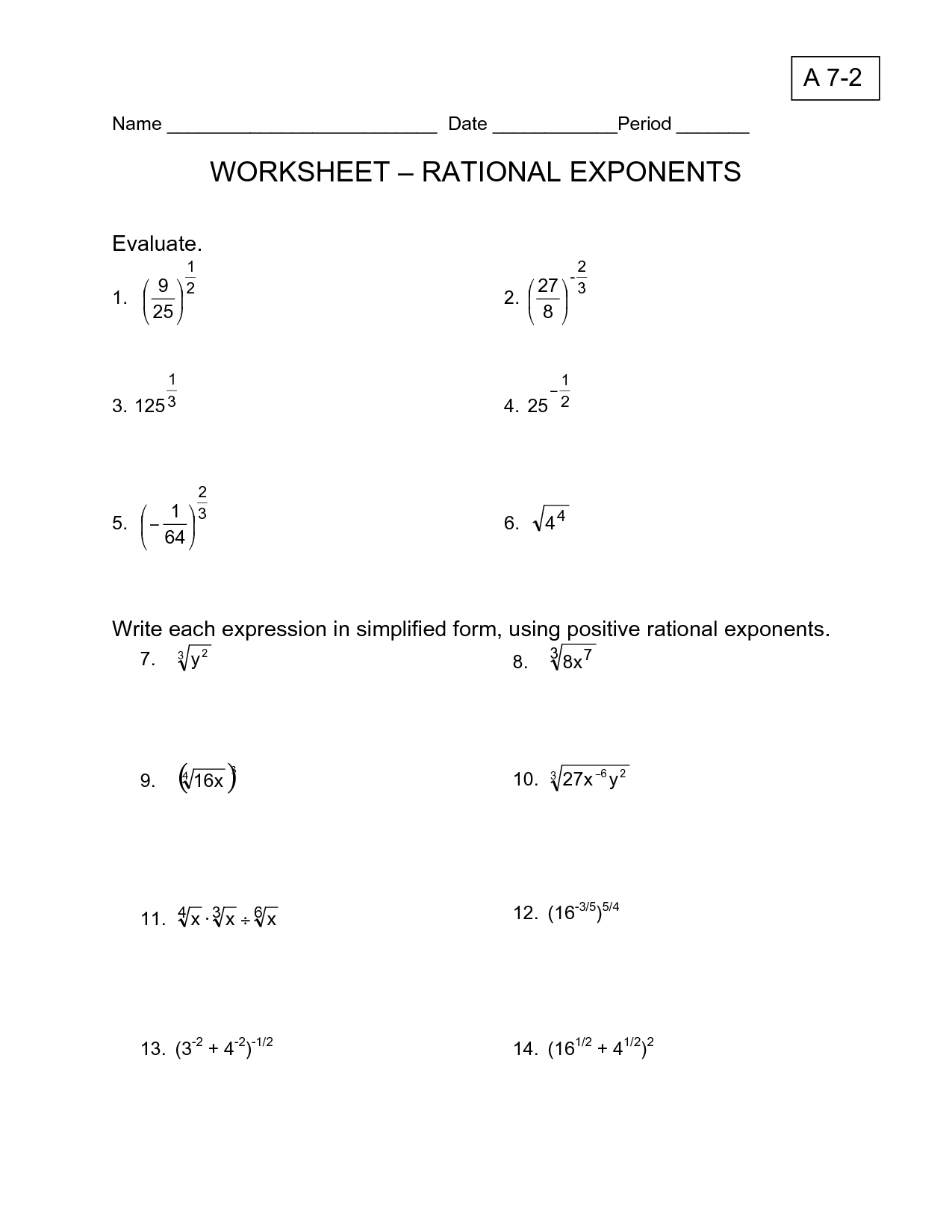
Rational exponents often come in forms that can be simplified. Practice converting between radical form and rational exponents:
- Convert (a^{\frac{1}{n}}) to (\sqrt[n]{a}).
- Use properties like ((a^m)^n = a^{mn}) to simplify expressions.
Here’s an example:
| Expression | Simplified Form |
|---|---|
| ((27^{\frac{1}{3}})^2) | 32 = 9 |

Tip 3: Leverage Worksheets for Diverse Problems

Worksheets offer a plethora of scenarios to solidify your understanding:
- Varied Examples: Include problems that involve exponents of fractions, negative exponents, and multiple operations.
- Real-life Applications: Work on problems that link rational exponents to real-world contexts, enhancing both understanding and interest.
⚙️ Note: Worksheets should be comprehensive to challenge and expand your knowledge.
Tip 4: Utilize Technology and Tools

Modern tools can significantly aid in learning:
- Calculators: Use scientific or graphing calculators to verify your calculations or check your work.
- Educational Software: Programs like GeoGebra or Desmos allow for interactive learning and exploration of rational exponents.
Tip 5: Regular Review and Reflection

Consistency is key in mastering any mathematical topic:
- Daily Practice: Dedicate time each day to work on rational exponents problems.
- Review Mistakes: Analyze your errors to understand where you need improvement.
- Set Goals: Gradually increase the complexity of problems you tackle.
Summing up, mastering rational exponents requires a blend of understanding fundamentals, consistent practice, and the strategic use of resources. By following these tips and dedicating yourself to the process, you'll not only conquer rational exponents but also enhance your overall mathematical proficiency. Remember, every small step in your learning journey builds upon the last, creating a strong foundation for more advanced math concepts.
Why are rational exponents important in mathematics?
+
Rational exponents are crucial because they allow for a seamless transition between different forms of mathematical expressions, making operations like differentiation, integration, and solving equations more intuitive and streamlined.
How do I know if I’m simplifying rational exponents correctly?
+
A good indicator is to check if your final answer matches or can be derived back into the original form. Using a calculator to verify can also help confirm your simplification.
Can I use these techniques in real-world applications?

+
Definitely! Rational exponents are used in fields like engineering, physics, and finance where exponential growth, decay, and roots are common, making them invaluable for solving complex problems.