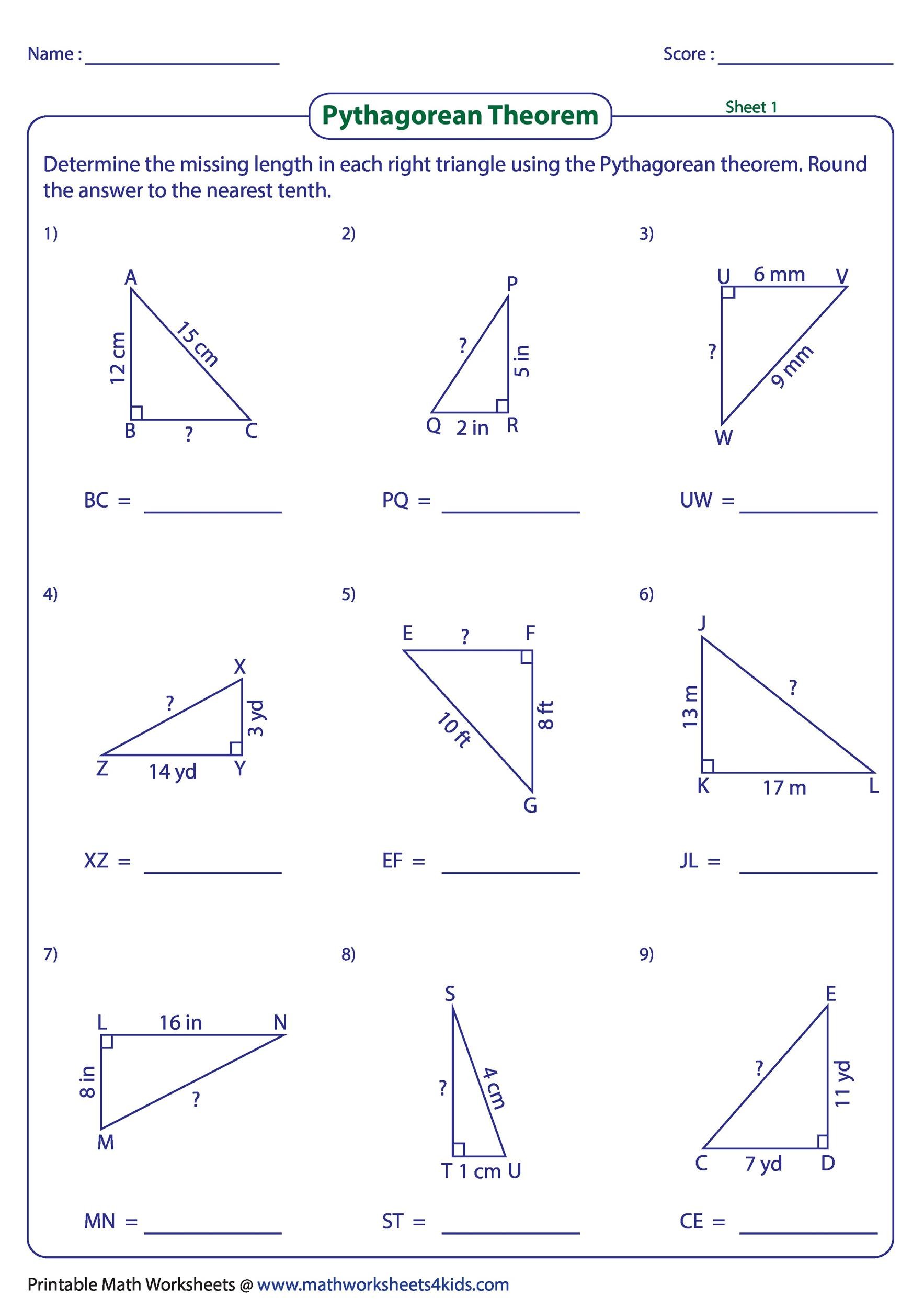
5 Easy Steps to Solve Pythagorean Theorem Worksheets

The Pythagorean Theorem is a cornerstone of mathematics, especially in geometry, making it an essential topic for students to master. Here’s how to conquer those Pythagorean Theorem worksheets with ease:
Understanding the Basics

Before you dive into solving problems, it's crucial to understand what the Pythagorean Theorem is. Known since ancient times, this theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. Mathematically, it's expressed as:
a² + b² = c²
Where:
- a and b are the lengths of the triangle's legs.
- c is the length of the hypotenuse.
Step-by-Step Guide to Solving Pythagorean Theorem Problems

Step 1: Identify the Triangle’s Sides

Most Pythagorean Theorem worksheets will present you with either the lengths of two sides or one side and the hypotenuse. Start by:
- Labeling the sides as a, b, or c. Remember, c is always the longest side.
- If two sides are given, you might need to solve for the third side.
Step 2: Apply the Theorem

Depending on which side you’re solving for:
- If you know a and b, calculate c using c = √(a² + b²).
- If you know c and one leg, solve for the other leg using a = √(c² - b²) or b = √(c² - a²).
Step 3: Plug in the Values

Substitute the known values into the equation:
- Ensure you keep track of which side is which!
Step 4: Solve the Equation

Perform the necessary calculations:
- For finding the hypotenuse or a leg, take the square root of both sides after squaring.
Step 5: Check Your Answer

After solving, it’s beneficial to:
- Check if your result makes sense within the context of the triangle.
- Use the theorem again, but with your calculated side to confirm if a² + b² = c² holds true.
💡 Note: Always keep units consistent when solving. If one side is measured in centimeters, all sides should be in centimeters.
Common Pitfalls

Here are some common mistakes to avoid:
- Not correctly identifying which side is the hypotenuse.
- Misapplying square roots or squares.
- Not rounding correctly if the problem specifies.
Advanced Tips for Quick Solving

To speed up your problem-solving:
- Memorize common squares and their roots (e.g., 3² = 9, 5² = 25).
- Estimate before calculating to check if your result seems reasonable.
📝 Note: Practicing with various worksheet types can help you identify and correct your common mistakes.
By following these steps, you can effectively and accurately solve Pythagorean Theorem problems, turning those daunting worksheets into an opportunity for growth. Remember, practice makes perfect, and with consistent effort, you'll not only become adept at solving these problems but also gain a deeper appreciation for this fundamental mathematical principle.
Why is the Pythagorean Theorem important?

+
The Pythagorean Theorem is foundational in understanding not just geometry but also real-world applications like architecture, navigation, and physics. It’s crucial for understanding distances, calculating heights, and even in computer graphics for 3D modeling.
What if I have only one side of the triangle?
+
If you have only one side, you cannot solve for the other sides using the Pythagorean Theorem alone. You’ll need additional information or another triangle property to proceed.
Can I use the Pythagorean Theorem on non-right triangles?

+
No, the Pythagorean Theorem applies strictly to right-angled triangles. For other triangles, you would use different methods like the law of cosines or sines.