5 Tips to Master Improper Fractions Easily

Understanding improper fractions can seem like a daunting task at first, but with the right approach, mastering them can become straightforward and even enjoyable. Improper fractions are those where the numerator is larger than the denominator, which means they represent values greater than one. Here's how you can quickly grasp and confidently handle improper fractions:
1. Understand the Basics
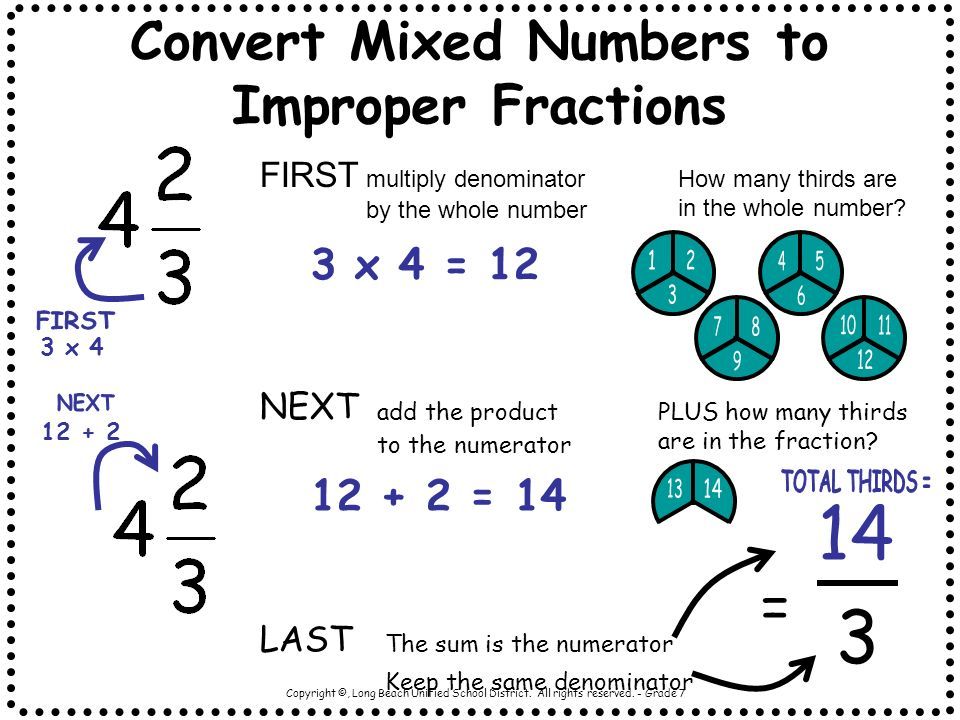
To handle improper fractions effectively, you need to know:
- Numerator: The top number in a fraction, which represents how many parts you have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
- Improper Fraction: A fraction where the numerator is greater than the denominator (e.g., 5⁄4).
Begin by reviewing the concepts of fractions in general. If you can work with proper fractions (where the numerator is less than the denominator), you're halfway there.
2. Convert Improper Fractions to Mixed Numbers

One of the most useful skills in dealing with improper fractions is converting them into mixed numbers. A mixed number combines a whole number with a fraction. Here’s how to convert an improper fraction into a mixed number:
- Divide: Divide the numerator by the denominator.
- Identify: The quotient becomes the whole number.
- Remainder: The remainder becomes the numerator of the new fraction, with the original denominator staying the same.
For example, to convert 7/4 to a mixed number:
- 7 ÷ 4 = 1 remainder 3
- So, 7/4 = 1 3/4
💡 Note: Understanding how to convert improper fractions into mixed numbers is key for simplifying and comparing fractions with whole numbers.
3. Simplify Improper Fractions

Simplifying fractions involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by this number. Here’s how to simplify an improper fraction:
- Find the GCD of the numerator and the denominator.
- Divide both the numerator and the denominator by the GCD.
For instance, to simplify 12/8:
- GCD of 12 and 8 is 4
- 12 ÷ 4 = 3
- 8 ÷ 4 = 2
- So, 12/8 simplifies to 3/2
4. Practice with Real-life Examples

Practice is essential in mastering any mathematical concept:
- Use practical scenarios like dividing pizzas among friends or sharing cookies to understand how fractions work in real life.
- Create visual aids or use manipulatives like fraction strips or pie charts to visualize and compare improper fractions.
Here's a simple exercise you can use to practice:
| Fraction | Problem | Solution |
|---|---|---|
| 5/3 | Convert to mixed number | 1 2/3 |
| 9/2 | Simplify | 4 1/2 |
| 14/6 | Convert and Simplify | 2 1/3 |

📚 Note: Real-world examples make abstract concepts tangible and easier to understand.
5. Use Online Resources and Apps
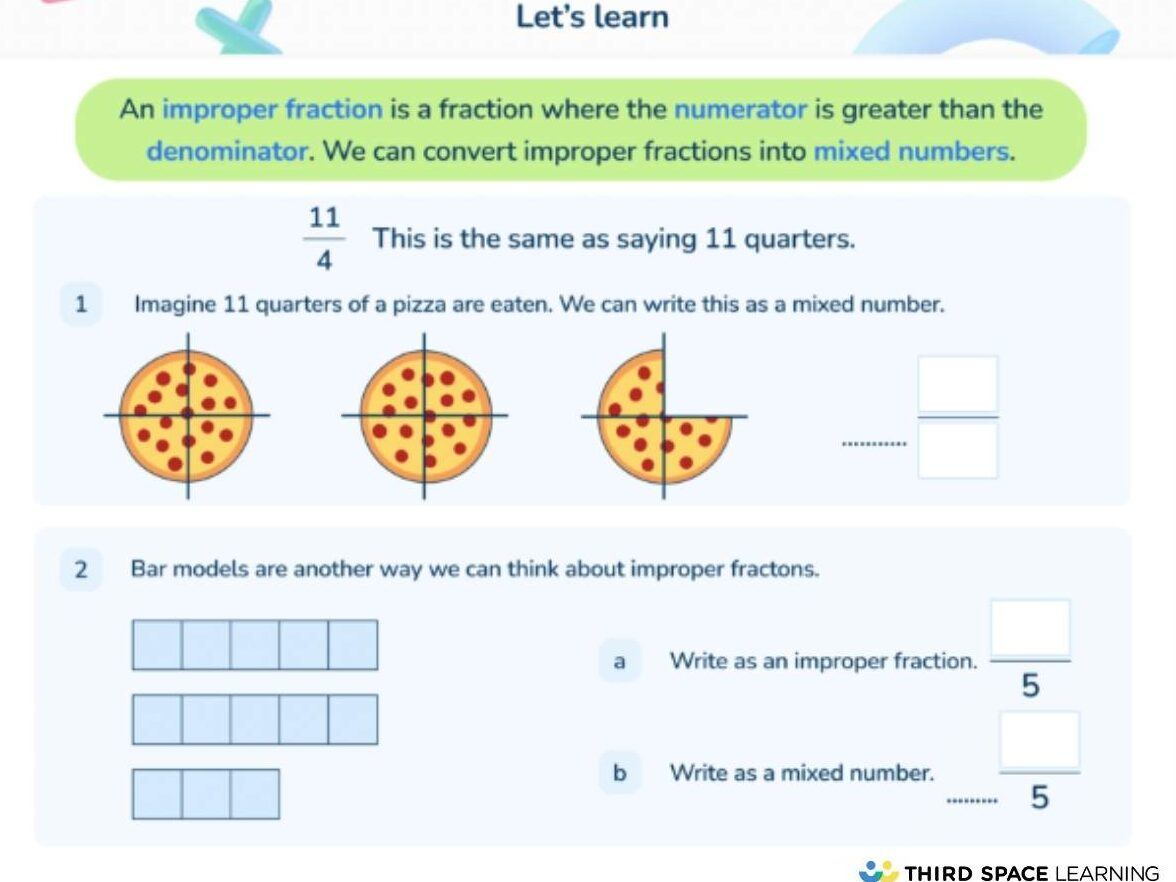
Technology provides a plethora of tools to aid in learning improper fractions:
- Use educational websites like Khan Academy, Math Playground, or IXL which offer interactive lessons and exercises.
- Consider math apps like Photomath or MyScript Calculator, where you can input your improper fraction problems to receive step-by-step solutions.
- Watch instructional videos on platforms like YouTube, which provide visual explanations and real-life problem-solving techniques.
In conclusion, mastering improper fractions requires understanding their basic components, knowing how to convert and simplify them, practicing regularly with real-world scenarios, and utilizing modern technology for learning support. With these tips, improper fractions can become an area of strength rather than a point of confusion.
Why are improper fractions important?

+
Improper fractions are crucial because they allow us to represent numbers greater than one in fraction form, which is useful in various mathematical operations and real-life problem-solving scenarios.
Can I always convert improper fractions to mixed numbers?

+
Yes, any improper fraction can be converted into a mixed number. This conversion helps in visualizing the fraction as a combination of whole numbers and a part.
How do I know if my improper fraction is simplified?

+
An improper fraction is simplified if the numerator and the denominator share no common factors other than 1. You can check this by ensuring their GCD is 1.
What’s the difference between simplifying and converting improper fractions?

+
Simplifying involves reducing the fraction to its lowest terms, while converting changes the form from an improper fraction to a mixed number or vice versa, maintaining the fraction’s value.