Complementary and Supplementary Angles Worksheet Made Easy

Understanding Complementary and Supplementary Angles

In geometry, angles play a crucial role in understanding various shapes and figures. Among the different types of angles, complementary and supplementary angles are two fundamental concepts that every student should grasp. In this article, we will delve into the world of complementary and supplementary angles, exploring their definitions, properties, and real-world applications.
What are Complementary Angles?

Complementary angles are two angles whose sum equals 90 degrees. In other words, when you add two complementary angles together, they form a right angle (90 degrees). For example, if you have an angle of 30 degrees, its complementary angle would be 60 degrees, since 30 + 60 = 90.
What are Supplementary Angles?

Supplementary angles are two angles whose sum equals 180 degrees. When you add two supplementary angles together, they form a straight angle (180 degrees). For instance, if you have an angle of 45 degrees, its supplementary angle would be 135 degrees, since 45 + 135 = 180.
Properties of Complementary and Supplementary Angles

Complementary and supplementary angles have some unique properties that make them useful in various mathematical and real-world applications.
- Complementary Angles:
- The sum of two complementary angles is always 90 degrees.
- The two angles are adjacent to each other (share a common vertex).
- Supplementary Angles:
- The sum of two supplementary angles is always 180 degrees.
- The two angles can be adjacent to each other or non-adjacent.
Real-World Applications of Complementary and Supplementary Angles

Complementary and supplementary angles are not just limited to theoretical mathematics; they have numerous practical applications in various fields.
- Architecture: Complementary angles are used in designing buildings, bridges, and other structures to ensure stability and balance. Supplementary angles are used to create straight lines and right angles.
- Engineering: Complementary and supplementary angles are crucial in designing electronic circuits, mechanical systems, and optical instruments.
- Art and Design: Artists and designers use complementary and supplementary angles to create visually appealing compositions and patterns.
Complementary and Supplementary Angles Worksheet

Now that you have a good understanding of complementary and supplementary angles, it’s time to practice with a worksheet. Below is a sample worksheet to help you reinforce your knowledge.
Complementary Angles Worksheet:
| Angle 1 | Angle 2 | Complementary Angle |
|---|---|---|
| 30 | ? | 60 |
| 45 | ? | 45 |
| 20 | ? | 70 |
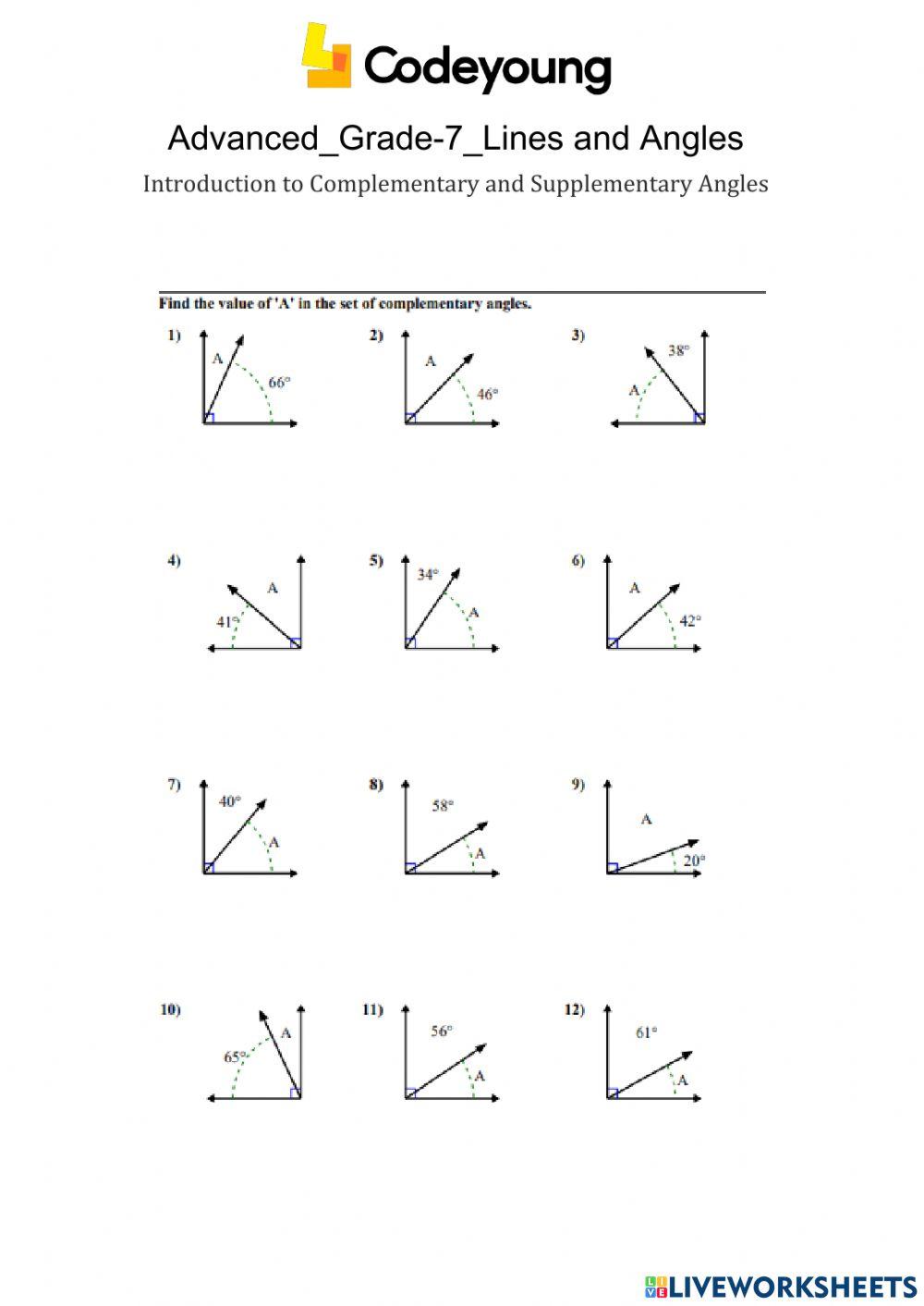
Supplementary Angles Worksheet:
| Angle 1 | Angle 2 | Supplementary Angle |
|---|---|---|
| 90 | ? | 90 |
| 120 | ? | 60 |
| 45 | ? | 135 |
Solving Complementary and Supplementary Angles

To solve the worksheets, follow these simple steps:
- Complementary Angles:
- Identify the given angle.
- Subtract the given angle from 90 degrees to find the complementary angle.
- Supplementary Angles:
- Identify the given angle.
- Subtract the given angle from 180 degrees to find the supplementary angle.
Example:
| Angle 1 | Angle 2 | Complementary Angle |
|---|---|---|
| 30 | 60 | 60 |
In this example, the given angle is 30 degrees. To find the complementary angle, subtract 30 from 90, which equals 60 degrees.
📝 Note: Make sure to check your answers carefully and use a calculator if necessary.
As you practice solving the worksheet, you’ll become more comfortable with complementary and supplementary angles. Remember to apply these concepts to real-world situations to deepen your understanding.
In conclusion, complementary and supplementary angles are fundamental concepts in geometry that have numerous practical applications. By understanding their properties and using the worksheets provided, you’ll become proficient in solving problems involving these angles.
What is the difference between complementary and supplementary angles?

+
Complementary angles are two angles whose sum equals 90 degrees, while supplementary angles are two angles whose sum equals 180 degrees.
Can two complementary angles be equal?

+
Yes, two complementary angles can be equal, and in that case, they would both be 45 degrees.
How are complementary and supplementary angles used in real-world applications?

+
Complementary and supplementary angles are used in architecture, engineering, art, and design to create stable structures, visually appealing compositions, and precise mechanical systems.
Related Terms:
- complementary angle worksheet pdf
- complementary angles worksheet with answers
- supplementary angles anchor chart
- complementary angles anchor chart
- complementary and supplementary angles solver
- complementary angles worksheet 4th grade