5 Tips to Master Inscribed Angles and Arcs
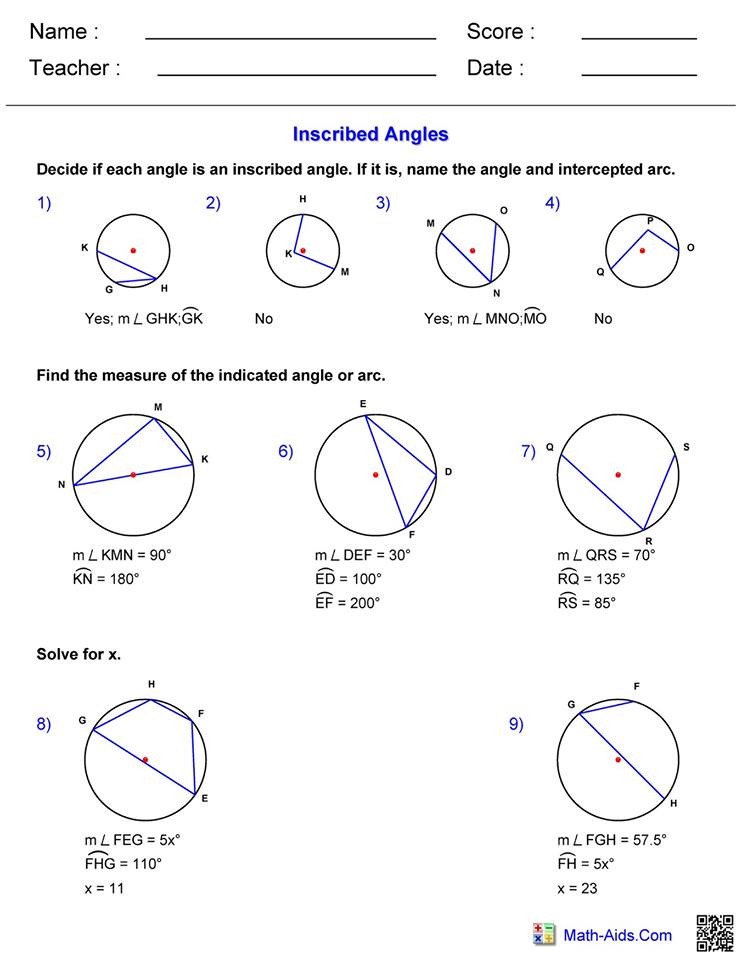
Understanding inscribed angles and arcs can be a fascinating journey into the world of geometry. Whether you're a student tackling these concepts for the first time or an enthusiast looking to deepen your mathematical knowledge, mastering these elements can enhance your geometric prowess. Here, we'll explore five key tips that can help you excel in the study of inscribed angles and arcs.
1. Understand the Basics

The foundation of learning about inscribed angles and arcs starts with understanding their definitions:
- Inscribed Angle: An angle whose vertex lies on the circle, and its sides contain chords of the circle.
- Central Angle: An angle whose vertex is at the center of the circle, and its sides contain radii of the circle.
- Arc: A part of the circumference of the circle, defined by an angle’s two endpoints on the circle.
💡 Note: Remember, the measure of an inscribed angle is half the measure of the arc it intercepts.
2. Visualize Through Diagrams

Geometry is a visual subject. Drawing accurate diagrams:
- Helps in understanding the relationships between inscribed angles, central angles, and arcs.
- Allows you to see how changing one element affects others.
| Element | Description |
|---|---|
| Central Angle | Equal to the arc it intercepts. |
| Inscribed Angle | Half the arc it intercepts. |

Spend time practicing the construction of these angles and arcs. This practice will solidify your understanding and improve your problem-solving skills.
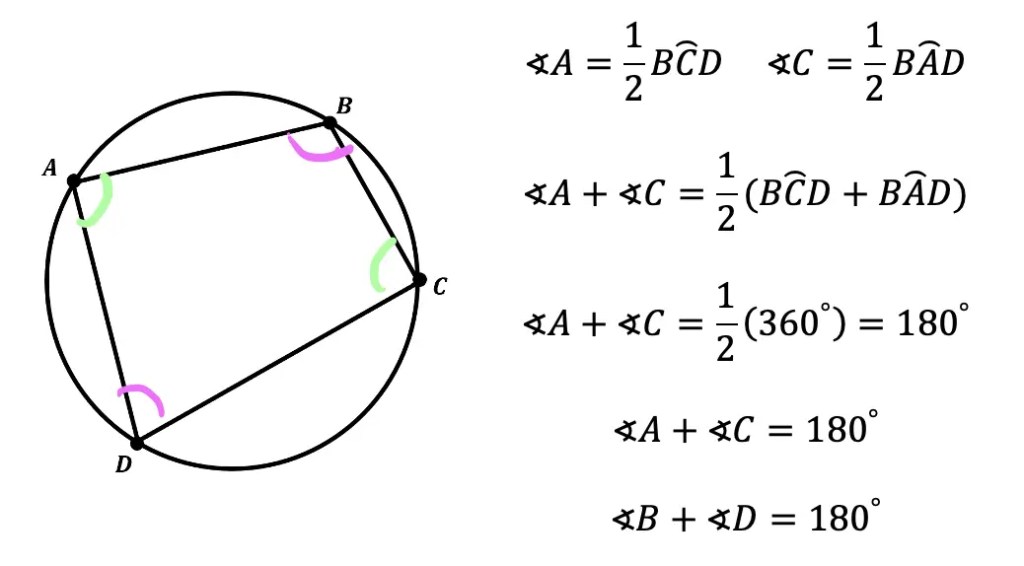
3. Use Relationships Between Angles
Circles come with a treasure trove of relationships:
- Angles formed by chords intersecting inside the circle.
- Angles formed by tangents and secants.
- Power Theorems: These relate the lengths of chords, tangents, and secants.
Here’s a handy relationship:
- An inscribed angle is half the measure of the arc it intercepts.
- A central angle equals the arc it intercepts.
🔍 Note: Use these relationships to solve for unknown angles or arcs in complex problems.
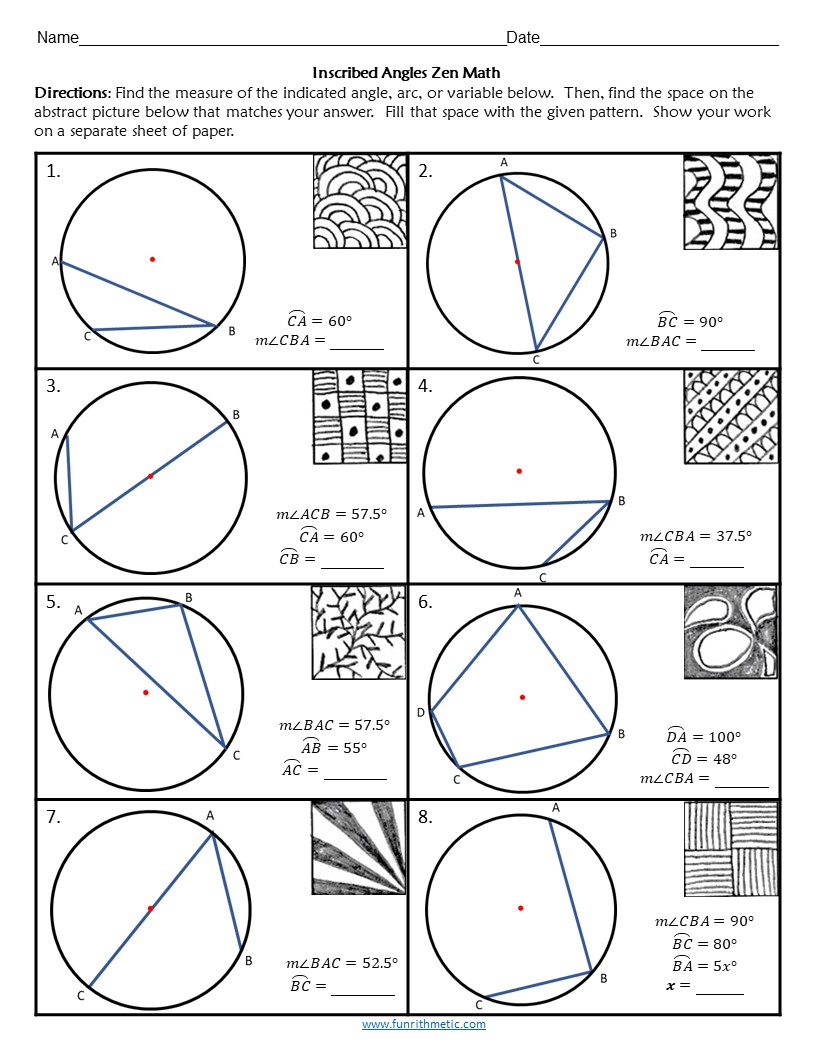
4. Practice with Multiple Configurations

To master inscribed angles and arcs:
- Practice problems where angles are inscribed within different arcs.
- Solve for angles when chords or tangents are involved.
- Work on scenarios involving multiple intersecting chords or tangents.
Below is an example of such a scenario:

5. Connect Concepts with Real-World Examples

Geometry isn’t just for the classroom. Here are some real-world applications:
- Architecture: Architects use arcs and angles to design structures like arches, domes, and curved facades.
- Design: In graphic design, understanding arcs and angles helps in creating logos or layouts with curves and circular elements.
- Engineering: Engineers rely on these principles for calculations in the design of gears, pistons, and other circular components.
Summing Up Key Points

Mastering inscribed angles and arcs involves a deep understanding of basic definitions, leveraging visual aids, knowing and applying angle relationships, practicing various geometric configurations, and connecting the concepts to real-world scenarios. By following these tips, you not only prepare yourself for complex geometric problems but also gain a holistic view of how geometry shapes our world.
Why is understanding inscribed angles important?

+
Inscribed angles are crucial because they help in solving problems related to circles, understanding architectural designs, and even analyzing engineering models where curves are involved.
Can the measure of an inscribed angle ever be larger than 90 degrees?

+
No, the measure of an inscribed angle can never exceed 90 degrees because it is half the measure of the intercepted arc, and no arc can span more than a semicircle (180 degrees).
How do I know which angle to find when solving a problem with inscribed angles?

+
Identify the type of angle or arc you need to solve for. Use the given information and apply the appropriate relationships between angles and arcs to work out the problem systematically.
Can an inscribed angle intercept more than one arc?

+
Yes, an inscribed angle can intercept multiple arcs if the sides of the angle extend to form different segments of the circle, but the primary arc it relates to is the one directly between its endpoints.



