7 Tips to Solve Momentum Conservation Worksheets Easily

In the realm of physics, momentum conservation is a principle that often puzzles students. Worksheets that require you to apply this principle can be particularly challenging if you're not familiar with the core concepts or lack a structured approach. This post will delve into seven effective tips that can help you easily navigate and solve momentum conservation worksheets.
1. Master the Basics

Before you dive into solving momentum conservation problems, ensure you have a solid grasp of the foundational concepts:
- Definition of Momentum: Momentum (p) is defined as mass times velocity (p = m × v).
- Conservation of Momentum: In an isolated system, the total momentum before an event (like a collision) equals the total momentum after the event.
- Elastic and Inelastic Collisions: Understand the differences and the implications for momentum and kinetic energy.
💡 Note: The principle of momentum conservation holds true only in an isolated system, where no external forces act on the system.
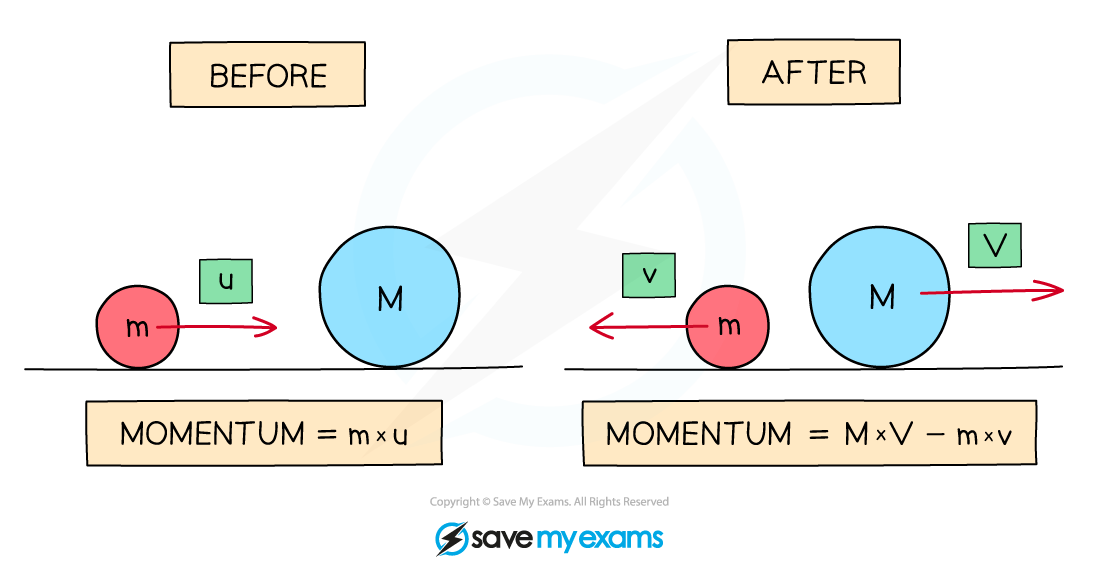
2. Visualize the Problem

Many students find it easier to understand and solve problems when they can visualize them:
- Draw a simple diagram representing the objects before and after the event.
- Include arrows to indicate direction and magnitude of velocities.
- Label masses, velocities, and any other relevant information.
3. Use Equations Wisely

The following equations are crucial for solving momentum conservation problems:
| Scenario | Equation |
|---|---|
| Total Momentum Before Collision | p_before = m_1 × v_1 + m_2 × v_2 |
| Total Momentum After Collision | p_after = m_1 × v_1’ + m_2 × v_2’ |
| Conservation of Momentum | p_before = p_after |

Remember, in elastic collisions, kinetic energy is also conserved, adding another equation to your arsenal.
4. Identify the System

To accurately apply momentum conservation, you must:
- Identify the objects in your system clearly.
- Decide if the system is isolated or not (considering external forces like friction or applied forces).
- Establish boundaries within which you’ll conserve momentum.
5. Break Down Problems into Steps

Complex problems can be made more manageable by breaking them into smaller, sequential steps:
- Determine the initial state: masses, velocities, and direction.
- Calculate the initial total momentum of the system.
- Identify the nature of the collision (elastic or inelastic).
- Set up the conservation of momentum equation.
- Solve for unknowns, keeping track of vectors and signs.
- Check your results for physical feasibility (e.g., conservation of energy in elastic collisions).
6. Use Dimensional Analysis

Ensuring that your equations and units are consistent:
- Momentum is measured in kg·m/s.
- Check if your units cancel out to give momentum units.
- Dimensional analysis can catch errors in your calculations.
7. Practice with Real-World Scenarios

Applying momentum conservation to real-world problems not only helps with understanding but also with retention:
- Study collision scenarios in sports (e.g., billiards or carom).
- Analyze accidents or laboratory experiments involving collisions.
- Use online simulations or momentum conservation apps for interactive learning.
By following these seven tips, you'll find yourself more adept at solving momentum conservation worksheets. The key is not just in learning the formulas but understanding their application in diverse physical scenarios. This understanding will transform your ability to approach, analyze, and solve problems in momentum conservation, making your learning journey both effective and enriching.
What is the difference between elastic and inelastic collisions?
+
In an elastic collision, both momentum and kinetic energy are conserved. Objects bounce off each other with no loss of energy. In an inelastic collision, momentum is conserved, but kinetic energy is not; the colliding objects tend to stick together or deform, reducing kinetic energy.
How do you know if a system is isolated?

+
A system is isolated if there are no external forces acting upon it during the event in question. This means that only internal forces (like those between colliding objects) are considered.
Why is direction important in momentum conservation?

+
Momentum is a vector quantity, meaning it has both magnitude and direction. Conservation of momentum requires that we take into account the direction of velocities when calculating total momentum before and after a collision. Positive or negative signs are used to represent these directions.