5 Simple Ways to Calculate Triangle Area

Learning how to calculate the area of a triangle is fundamental in geometry, and understanding this can aid in various professional fields such as architecture, engineering, or even interior design. Here, we explore five simple methods to compute the area of a triangle, catering to different shapes and available data. Let's dive in.
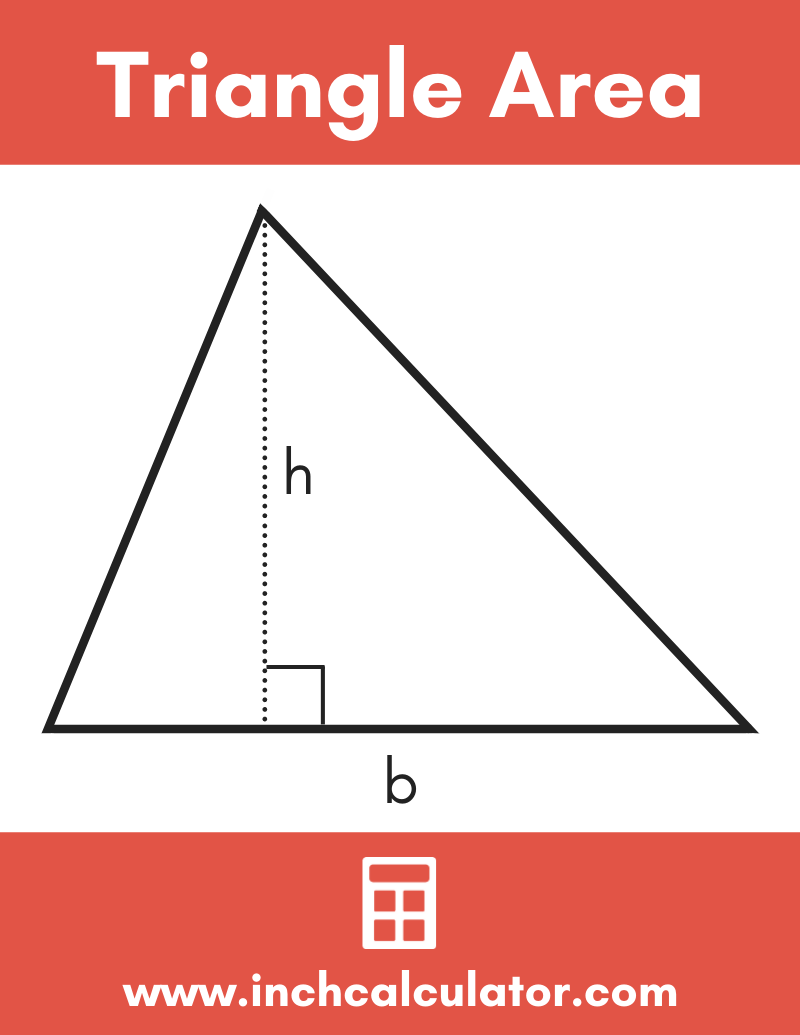
1. Base and Height Method

The most straightforward method involves using the base and the height of a triangle. This method is commonly used for right triangles, but it can apply to any triangle where the height is perpendicular to the base.
- Identify the base of the triangle.
- Measure the height, which is a perpendicular line from the base to the opposite vertex.
- Use the formula: Area = (Base × Height) / 2.

📏 Note: Make sure the height is always perpendicular to the base, or your calculation will be incorrect.
2. Heron's Formula
Heron's Formula, also known as Hero's formula, is particularly useful when you know the length of all three sides of the triangle.
- First, calculate the semi-perimeter s by adding all three sides and dividing by 2: s = (a + b + c) / 2.
- Then, plug the values into Heron's formula:
Area = √[s(s - a)(s - b)(s - c)]

📝 Note: Heron’s formula works for all types of triangles, including scalene, isosceles, and equilateral triangles.
3. Using Trigonometry (with Two Sides and the Included Angle)

When you know two sides of the triangle and the included angle, trigonometry provides an excellent approach to calculate the area.
- Identify two sides of the triangle, let’s call them a and b, and the angle between them θ.
- Apply the formula:
Area = (1/2) × a × b × sin(θ)

4. Equilateral Triangle Area

For an equilateral triangle, where all sides are equal, the calculation is simplified since the height forms a right angle with one of the sides.
- Calculate the height of the triangle using h = (√3 / 2) × side length.
- Then, use the standard area formula: Area = (Base × Height) / 2.
| Side Length (s) | Height (h) | Area |
|---|---|---|
| 10 units | (√3 / 2) × 10 ≈ 8.66 units | (10 × 8.66) / 2 = 43.3 square units |

5. Using Coordinates

When the vertices of the triangle are given as coordinates on a plane, you can calculate its area using determinant algebra or geometric mean.
- Let’s denote the vertices as A(x1, y1), B(x2, y2), and C(x3, y3).
- Use the determinant formula:
Area = | (x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2))/2 |
In summary, understanding how to calculate the area of triangles through these methods empowers you to tackle various geometric problems. Each method has its strengths:
- The base and height method is simple but requires perpendicularity.
- Heron's formula can be used with any triangle where side lengths are known.
- Trigonometry provides flexibility when angles are involved.
- Equilateral triangles offer an easy formula due to their symmetrical properties.
- Coordinate geometry offers precision when dealing with graphical representations.
With these techniques in your toolkit, you're ready to approach geometric tasks with confidence, whether it’s for practical design or theoretical math. Remember, the key to mastering these calculations lies in understanding the context of the data you have and selecting the most fitting method.
Can I use the base and height method for all triangles?

+
Yes, but you must ensure the height is perpendicular to the base. For non-right triangles, you might need to calculate the height separately.
When should I use Heron’s Formula?

+
Use Heron’s Formula when you know the lengths of all three sides of the triangle and don’t have the height or angle information.
Is trigonometry always needed for triangle area calculation?

+
No, trigonometry is useful when you know two sides and the included angle, but other methods are often easier and applicable in different scenarios.