Area of Irregular Shapes Worksheet Made Easy
Unlocking the Secrets of Calculating the Area of Irregular Shapes

Calculating the area of irregular shapes can be a daunting task for many students. Unlike regular shapes, irregular shapes do not have symmetrical sides or angles, making it challenging to determine their area. However, with the right strategies and techniques, calculating the area of irregular shapes can be made easy.
What are Irregular Shapes?

Irregular shapes are polygons that do not have equal sides or equal angles. They can be triangles, quadrilaterals, pentagons, or any other polygon with unequal sides and angles. Irregular shapes are commonly found in real-life objects, such as buildings, bridges, and mountains.
Why is Calculating the Area of Irregular Shapes Important?

Calculating the area of irregular shapes is crucial in various fields, such as architecture, engineering, and geography. For instance, architects need to calculate the area of irregularly shaped rooms to determine the amount of flooring material needed. Engineers need to calculate the area of irregular shapes to determine the stress and strain on a structure. Geographers need to calculate the area of irregularly shaped landforms to understand the Earth’s surface.
Methods for Calculating the Area of Irregular Shapes

There are several methods for calculating the area of irregular shapes, including:
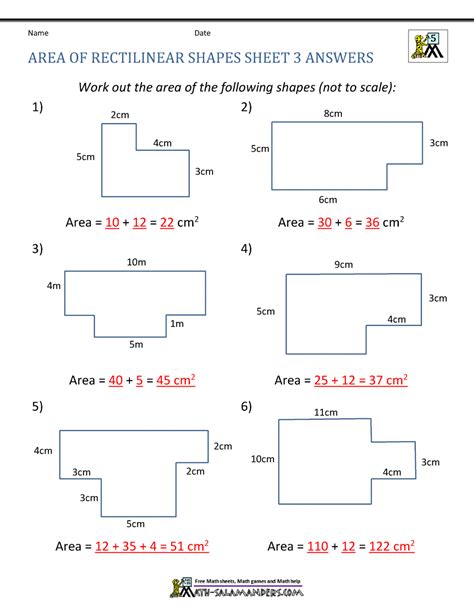
- Breaking down the shape into smaller regular shapes: This method involves dividing the irregular shape into smaller regular shapes, such as triangles or rectangles, and then calculating the area of each shape separately.
- Using the formula for the area of a polygon: This method involves using the formula for the area of a polygon, which is (n x s^2) / (4 x tan(π/n)), where n is the number of sides and s is the length of each side.
- Using the Shoelace formula: This method involves using the Shoelace formula, which is a mathematical formula for calculating the area of a polygon given its vertices.
Step-by-Step Guide to Calculating the Area of Irregular Shapes
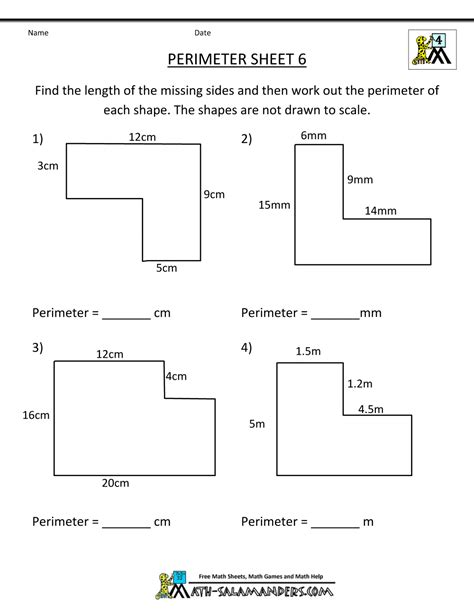
Here is a step-by-step guide to calculating the area of irregular shapes:
- Identify the shape: Identify the irregular shape and determine its number of sides and vertices.
- Break down the shape into smaller regular shapes: Divide the irregular shape into smaller regular shapes, such as triangles or rectangles.
- Calculate the area of each shape: Calculate the area of each regular shape using the formula for the area of a triangle or rectangle.
- Add up the areas: Add up the areas of each regular shape to find the total area of the irregular shape.
📝 Note: Make sure to use the correct formula for the area of each regular shape, and to add up the areas carefully to avoid errors.
Examples of Calculating the Area of Irregular Shapes

Here are some examples of calculating the area of irregular shapes:
- Example 1: Calculate the area of a quadrilateral with sides of 5 cm, 6 cm, 7 cm, and 8 cm.
- Break down the shape into two triangles and a rectangle.
- Calculate the area of each shape using the formula for the area of a triangle and rectangle.
- Add up the areas to find the total area of the quadrilateral.
- Example 2: Calculate the area of a hexagon with sides of 3 cm, 4 cm, 5 cm, 6 cm, 7 cm, and 8 cm.
- Break down the shape into six triangles.
- Calculate the area of each triangle using the formula for the area of a triangle.
- Add up the areas to find the total area of the hexagon.
Conclusion

Calculating the area of irregular shapes can be a challenging task, but with the right strategies and techniques, it can be made easy. By breaking down the shape into smaller regular shapes, using the formula for the area of a polygon, and using the Shoelace formula, you can calculate the area of irregular shapes with ease. Remember to always use the correct formula for the area of each regular shape, and to add up the areas carefully to avoid errors.
What is the difference between regular and irregular shapes?

+
Regular shapes have equal sides and equal angles, while irregular shapes do not have equal sides or equal angles.
What is the Shoelace formula?

+
The Shoelace formula is a mathematical formula for calculating the area of a polygon given its vertices.
Why is calculating the area of irregular shapes important?

+
Calculating the area of irregular shapes is crucial in various fields, such as architecture, engineering, and geography, to determine the amount of material needed, stress and strain on a structure, and to understand the Earth’s surface.
Related Terms:
- area of irregular shapes formula
- 3rd grade irregular shape worksheet
- perimeter worksheets for 6th grade
- irregular shapes area 3rd grade
- perimeter worksheets for grade 6
- solve irregular shapes area worksheet