Algebra Worksheet Answers: Unlocking Every Problem Easily

Algebra, a fundamental branch of mathematics, has long been a topic that both intimidates and fascinates students. Whether you're just starting out or grappling with advanced concepts, the key to mastering algebra lies in understanding its foundational concepts and solving problems efficiently. In this extensive guide, we will delve into algebra worksheet answers, offering strategies, tips, and explanations to unlock every algebra problem with ease.
The Basics of Algebra

Algebra isn’t just about solving for x; it’s a language used to express mathematical relationships and model real-world problems. Here are some basic concepts to start with:
- Variables: Symbols representing unknown quantities.
- Equations: Statements that two expressions are equal.
- Terms and Coefficients: Variables with their numerical multipliers.
Expressions

Algebraic expressions are the building blocks of algebra. An expression like 5x + 3 involves variables and constants combined using operations like addition, subtraction, multiplication, and division.
Solving Equations
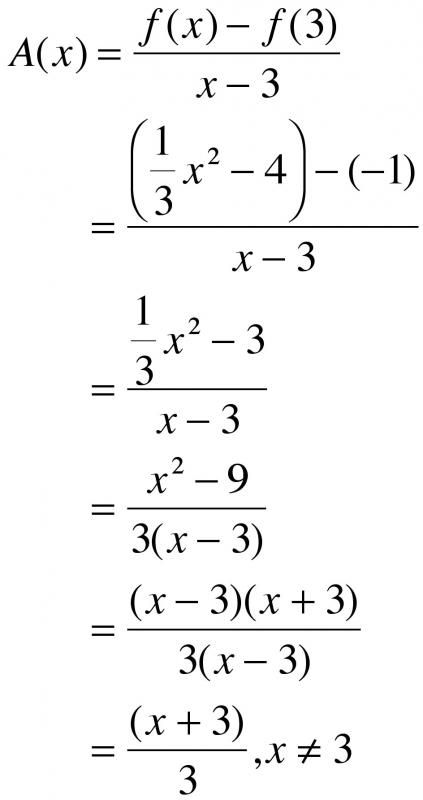
One of the primary goals in algebra is to solve equations. Here’s a step-by-step approach to tackle linear equations:
- Isolate the variable on one side of the equation.
- Eliminate constants by performing inverse operations (addition/subtraction).
- Eliminate coefficients by dividing both sides by the variable’s coefficient.
| Equation | Step | Operation |
|---|---|---|
| 2x + 3 = 11 | 1 | Subtract 3 from both sides: 2x = 8 |
| 2x = 8 | 2 | Divide both sides by 2: x = 4 |

Quadratic Equations

Quadratic equations take the form ax² + bx + c = 0. There are multiple methods to solve these:
- Factoring: If ax² + bx + c can be factored, set each factor equal to zero.
- Completing the square: Transform the equation to make a perfect square trinomial.
- Quadratic Formula: Use x = (-b ± √(b²-4ac)) / (2a) for any quadratic equation.
Common Algebraic Mistakes

Algebraic mistakes can lead to incorrect answers. Here are some common pitfalls to avoid:
- Distributing incorrectly during FOIL (First, Outer, Inner, Last).
- Forgetting to distribute multiplication through parentheses.
- Performing operations in the wrong order (not following PEMDAS/BODMAS).
- Misinterpreting signs when moving terms across the equation.
Practice Makes Perfect

Here are some strategies to practice algebra effectively:
- Start with basic problems and gradually move to complex ones.
- Use algebra software or apps for interactive learning.
- Join study groups to solve problems collaboratively.
- Time yourself to simulate exam conditions and improve efficiency.
💡 Note: Remember that algebra involves recognizing patterns and understanding why certain manipulations work.
As we wrap up this exploration of algebra worksheet answers, it's clear that mastering algebra is about consistent practice, understanding the concepts deeply, and applying techniques systematically. By focusing on the basics, avoiding common mistakes, and practicing with intention, algebra can transform from a subject of intimidation to one of empowerment. Whether you're solving for x, manipulating equations, or tackling quadratic problems, you now have the tools to approach each challenge with confidence. Let the journey into algebra be one where every problem is an opportunity to grow your mathematical prowess.
What are the main components of an algebraic expression?

+
The main components include variables (letters representing unknown quantities), constants (known numbers), coefficients (numbers before a variable), and operations (like addition or multiplication).
How do I check if my algebra answer is correct?

+
After solving an equation, substitute your answer back into the original equation to see if both sides balance. If they do, your answer is likely correct. Additionally, using algebraic software or apps can help verify solutions.
What is the importance of factoring in algebra?
+
Factoring helps in simplifying expressions, solving equations, and understanding the structure of polynomials. It’s crucial for finding roots, simplifying complex expressions, and in calculus for differentiation and integration.