Worksheet Adding Fractions With Unlike Denominators

Understanding how to add fractions with unlike denominators is essential for mastering basic arithmetic, making it a fundamental skill for students and useful for various real-life situations. Whether you're preparing a recipe, analyzing data, or solving mathematical problems, this knowledge can save time and reduce errors. Here’s a comprehensive guide on how to add fractions when their denominators are not the same.
Why Different Denominators Matter


Fractions are essentially portions of a whole, and when you want to combine these portions, the common base or denominator becomes crucial. Just as you can't directly add 1 apple and 2 oranges without considering their different kinds, you can't add fractions with different denominators without some adjustments.
The Concept of a Common Denominator

A common denominator is a shared multiple of the denominators of the fractions you are adding. Here's why it's important:
- Uniformity: It allows us to treat each fraction as part of the same whole.
- Accuracy: Ensures we add only the numerators, making our calculations precise.
- Simplicity: It simplifies the process by allowing us to work with a single 'unit' for both fractions.
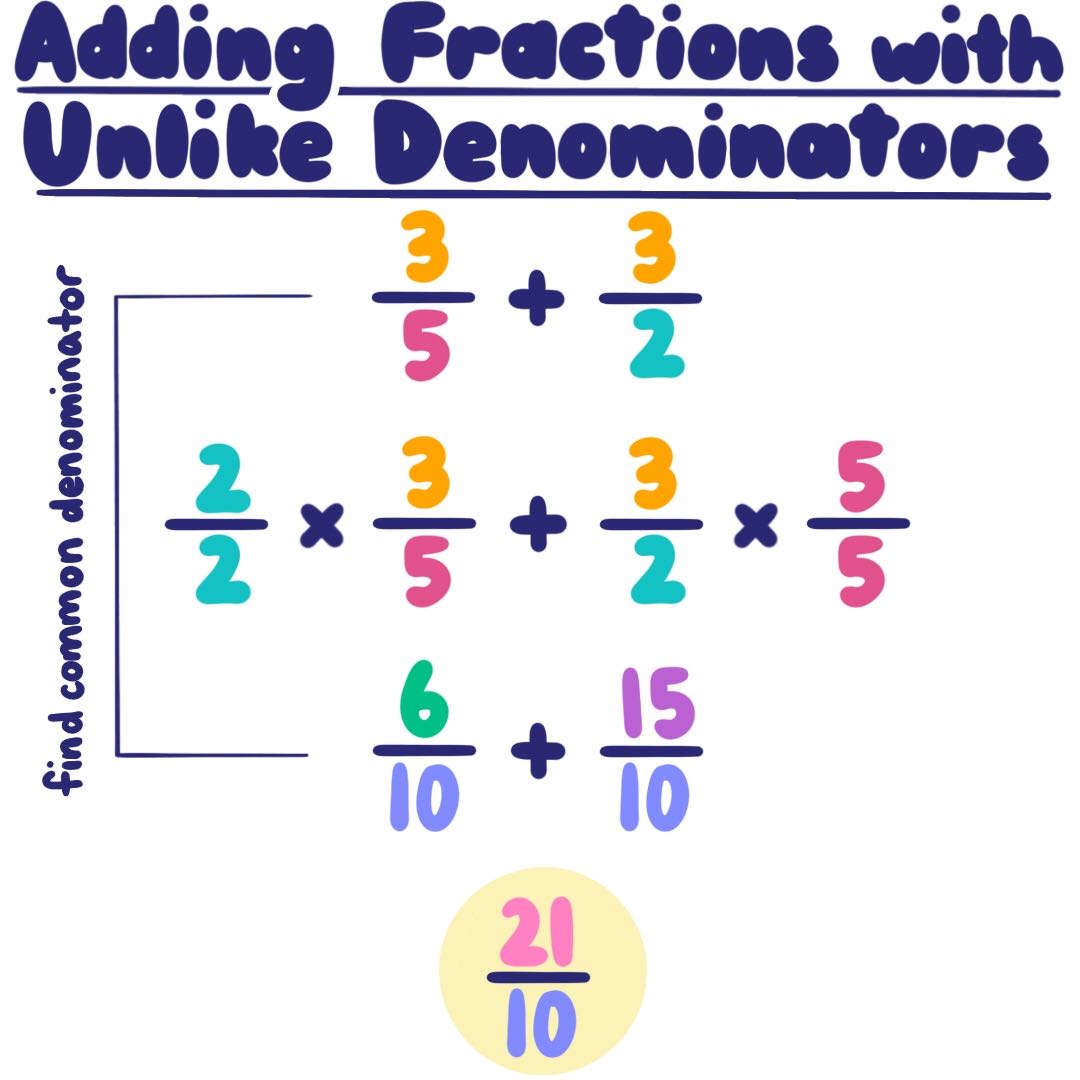
Steps to Add Fractions with Unlike Denominators

Find the Least Common Multiple (LCM)

To find a common ground for different fractions:
- List the multiples of each denominator.
- Identify the smallest number that both lists share, which is the LCM.
Convert Fractions to Like Denominators

Once you have the LCM:
- Divide the LCM by the denominator of each fraction.
- Multiply both the numerator and the denominator of each fraction by this quotient.
- Now, all fractions share the same denominator, and addition becomes straightforward.
Perform Addition

With common denominators in place:
- Add the numerators together.
- Keep the common denominator as is.
- Optionally, simplify the resulting fraction.
📚 Note: The use of LCM helps to minimize the denominator, ensuring efficiency and simplicity in your calculations.
Advanced Techniques for Adding Fractions
Using Prime Factorization for LCM

Finding LCM through prime factorization involves:
- Decomposing each denominator into its prime factors.
- Multiplying the highest power of all prime factors present in all denominators.
Adding Mixed Numbers

When dealing with mixed numbers:
- Convert mixed numbers to improper fractions.
- Follow the steps for adding unlike denominators.
- Convert the result back to a mixed number if necessary.
Shortcuts for Common Denominators

For fractions with denominators like 2, 3, 4, 5, etc.:
- Learn and apply common multiples (e.g., 12 for 3 and 4).
💡 Note: Practice with a variety of denominators to become familiar with frequent LCMs.
Real-World Applications of Adding Fractions

Cooking and Recipes

In culinary settings, precise measurements are key. Imagine needing to add 3⁄4 cup of water with 1⁄3 cup of oil:
| Fraction | Denominator | Converted |
|---|---|---|
| 3⁄4 | 4 | 9⁄12 |
| 1⁄3 | 3 | 4⁄12 |
| Sum: | 12 | 13⁄12 = 11⁄12 |

Financial Calculations

When budgeting or calculating interest, understanding how to add different portions can simplify the process. Consider adding a 1⁄2 savings rate with a 3⁄5 spending rate:
- LCM(2,5) = 10
- Converted fractions: 5⁄10 and 6⁄10
- Sum: 11⁄10 or 11⁄10
Mastering the addition of fractions with unlike denominators enriches one's mathematical repertoire, enhancing problem-solving skills in diverse contexts. This skill equips us to make sense of proportions, analyze data, and make informed decisions in various settings. From culinary arts to financial planning, understanding fractions is more than just academic; it's practically essential.
Adding fractions might seem intimidating at first, but through practice, understanding the process becomes intuitive. Here are some final thoughts to keep in mind:
How do you simplify the LCM for fractions with larger denominators?

+
Prime factorization is efficient for larger numbers. Find the highest power of common prime factors and multiply them.
Can you add fractions with negative numerators?
+
Yes, but ensure to consider the signs when summing. The sum can be negative if the absolute values of the numerators make the result smaller than the denominator.
What if the denominators are large primes?
+
Large prime denominators might require using the denominator as is if no smaller common multiple exists. However, finding the LCM can become computationally intensive.
How do you verify your results when adding fractions?
+
Convert the sum back to a mixed number or decimal equivalent, or cross-check by subtracting fractions to see if you return to the original numbers.