Master Adding and Subtracting Fractions with Ease
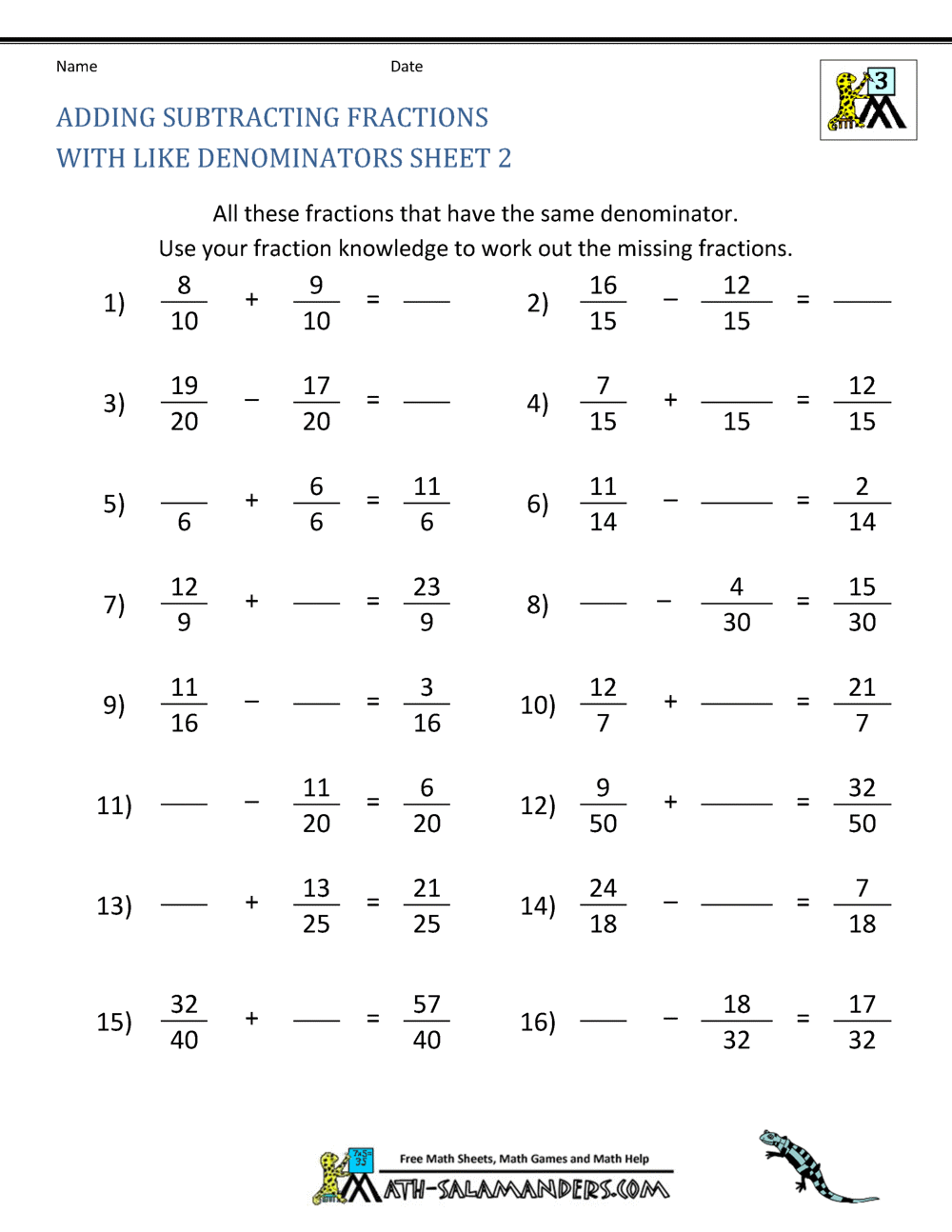
Understanding Fractions: A Primer

Before diving into adding and subtracting fractions, it’s crucial to understand what a fraction is and how it functions within the realm of mathematics. A fraction represents a part of a whole or, more precisely, a division of two numbers. For instance, 1⁄2 means one part out of two, indicating that half of something has been taken into account. Fractions consist of two main parts:
- Numerator: The top number, which indicates the quantity of parts we are considering.
- Denominator: The bottom number, showing into how many equal parts the whole has been divided.
Knowing these fundamental components allows us to work with fractions effectively, whether we are performing basic arithmetic operations like addition and subtraction, or dealing with more complex algebraic fractions.
Steps to Add Fractions

Adding fractions is an exercise in aligning denominators to ensure you can combine like terms. Here’s how you do it:
- Identify a common denominator. If the fractions you want to add already have the same denominator, you skip this step. Otherwise, you’ll need to find the least common multiple (LCM) of the denominators. For example:
- If you have fractions 1⁄2 and 3⁄4, the common denominator could be 4 (the LCM of 2 and 4).
- Adjust each fraction to have this common denominator. Multiply both the numerator and denominator of each fraction by the same number:
- 1⁄2 becomes (1*2)/(2*2) = 2⁄4.
- Add the numerators. After adjusting the fractions, simply add the numerators:
- 2⁄4 + 3⁄4 = (2 + 3)/4 = 5⁄4.
⚠️ Note: Simplify if necessary. After adding, if the resulting fraction can be simplified, do so to express it in its lowest terms.
Subtracting Fractions

Subtracting fractions follows a similar logic to addition:
- Find a common denominator. This step is identical to adding fractions.
- Adjust the fractions. If the denominators differ, convert each fraction so that they share the same denominator.
- Subtract the numerators. Now that the denominators are the same, subtract the top numbers:
- For 5⁄4 - 2⁄4, subtract 5 - 2 = 3 to get 3⁄4.
Adding Mixed Numbers

Mixed numbers are a combination of a whole number and a proper fraction, for example, 1 1⁄2. Adding mixed numbers involves:
- Convert mixed numbers into improper fractions or keep them as mixed numbers and add whole parts separately.
- Follow the same steps for adding fractions, then convert back if necessary.
For example:
- 1 1⁄2 + 2 3⁄4:
- Convert to improper fractions: 1 1⁄2 = 3⁄2 and 2 3⁄4 = 11⁄4.
- Find the LCM of denominators (4). Convert 3⁄2 = 6⁄4.
- Add 6⁄4 + 11⁄4 = 17⁄4.
- Convert back to mixed numbers: 17⁄4 = 4 1⁄4.
Visual Representation for Adding and Subtracting Fractions


Utilizing Visual Aids

Visual aids can be a powerful tool for understanding and teaching the addition and subtraction of fractions:
| Operation | Visual Aid |
|---|---|
| Addition | Imagine two pies, one with 1⁄4 eaten and the other with 1⁄4 eaten. Together, you’ve eaten 2⁄4 or 1⁄2 of a pie. |
| Subtraction | Consider two pies again, with one pie having 3⁄4 left and the other 1⁄4 left. Subtracting means determining how much more is left in the first pie compared to the second, which would be 2⁄4 or 1⁄2. |
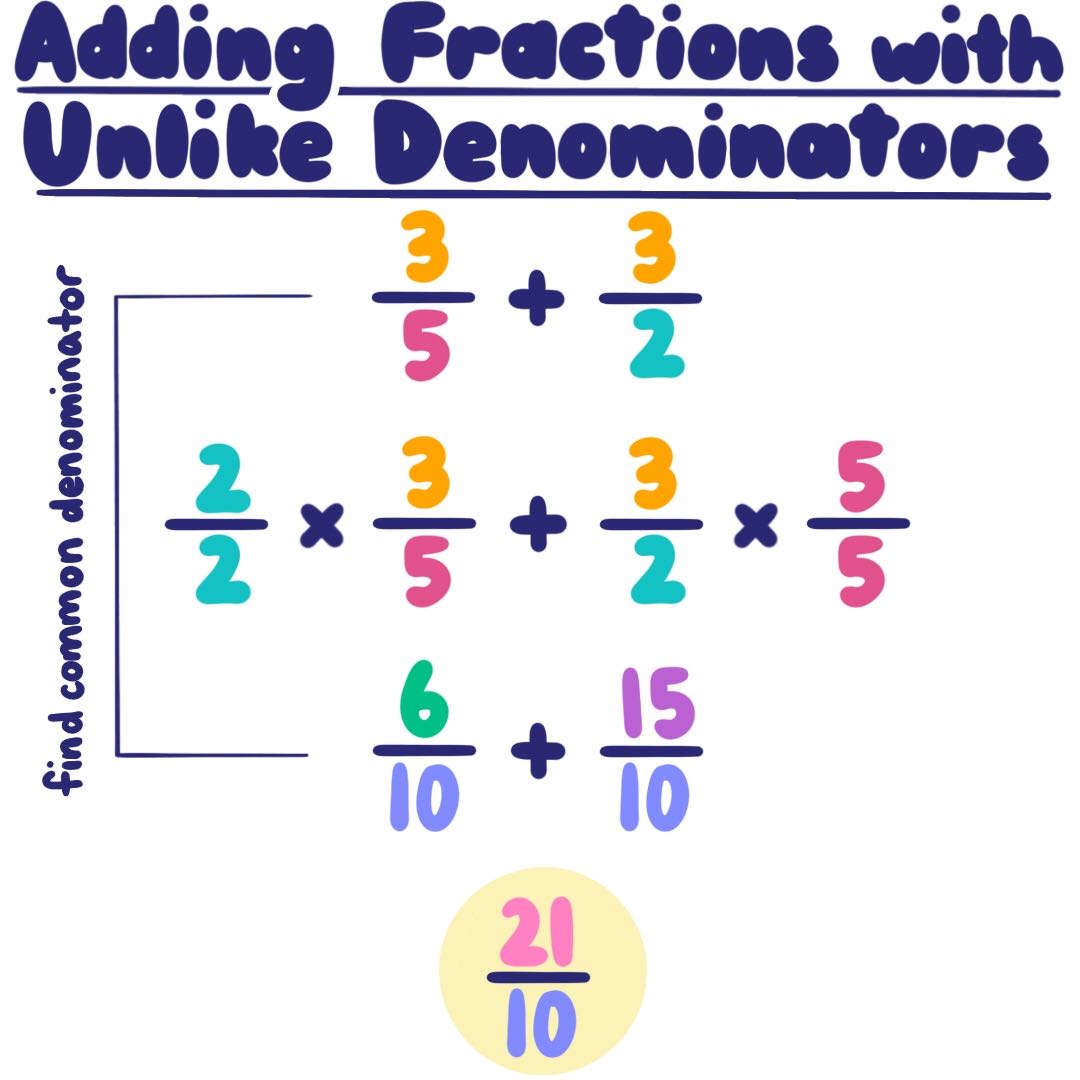
🧠 Note: Visual aids not only help in understanding the concept but also in retaining the information longer.
As we conclude our exploration into mastering the addition and subtraction of fractions, it's clear that while these operations might seem daunting initially, they are built on simple, logical principles. With a bit of practice, aligning denominators, adding or subtracting numerators, and converting between mixed numbers and improper fractions become second nature. This foundational arithmetic skill is not only vital for everyday calculations but also paves the way for understanding more complex mathematical concepts. Remember that practice makes perfect, and patience with oneself is key to mastering these operations. By embracing visual aids and consistent practice, you'll find yourself adding and subtracting fractions with ease, whether for educational purposes or practical applications.
Why do fractions need a common denominator?

+
Fractions need a common denominator to ensure that the numerators being added or subtracted represent the same part of the whole, allowing for a meaningful sum or difference.
Can I add or subtract fractions with different denominators without converting?

+
No, you must first convert fractions to have a common denominator because otherwise, the operation doesn’t make mathematical sense.
What if the fraction result can be simplified?

+
Always simplify the resulting fraction to express it in its lowest terms, which makes the number more manageable and easier to understand.