Parallel Lines Transversal Worksheet: Simple Guide

Geometry, with its myriad of shapes, angles, and lines, forms the backbone of many mathematical concepts and real-world applications. Among the fundamental topics in geometry, understanding how parallel lines behave when intersected by a transversal can sometimes feel like navigating a maze. However, with the right tools and a systematic approach, grasping these concepts becomes less of a puzzle and more of an adventure in logic. This blog post provides a comprehensive guide to understanding and creating a Parallel Lines Transversal Worksheet, ensuring both students and educators can utilize this resource effectively.
What Are Parallel Lines and a Transversal?
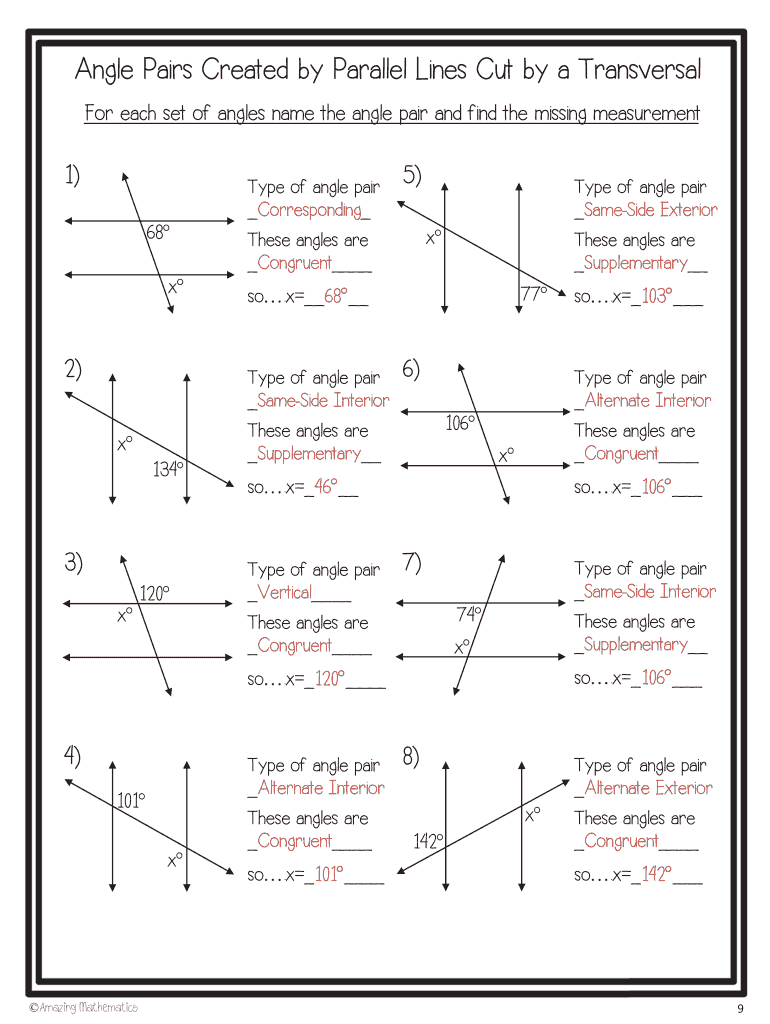
Parallel lines are two lines on a plane that never meet or intersect, keeping an equal distance apart at every point. A transversal is a line that cuts across two or more lines at distinct points. When a transversal intersects parallel lines, it creates several pairs of angles:
- Corresponding Angles: Angles that are on the same side of the transversal and in matching corners.
- Alternate Interior Angles: Angles that are between the parallel lines but on opposite sides of the transversal.
- Alternate Exterior Angles: Angles that are outside the parallel lines and on opposite sides of the transversal.
- Same Side Interior Angles (or Co-interior Angles): Angles that are inside the parallel lines and on the same side of the transversal.
Creating Your Parallel Lines Transversal Worksheet

To craft an effective worksheet, consider the following steps:
- Identify Objectives: Determine what you want students to learn from the worksheet. Is it identifying angles, calculating their measures, or understanding properties?
- Choose Your Format: Decide if it's going to be a fill-in-the-blank exercise, a matching activity, or a problem-solving task.
- Sketch the Diagram: Draw parallel lines intersected by a transversal. Clearly label angles.
- Prepare Questions: Create questions or tasks that align with your objectives. Here's how:
Basic Angle Identification

Start with simple questions:
- Identify the types of angles formed (corresponding, alternate interior, etc.).
- Label angles with their appropriate names or measurements if given.
Angle Calculation

If you provide an angle measure:
- Ask students to find the measures of other angles using properties like supplementary angles or vertical angles.
Problem Solving

Introduce scenarios where students must use logic:
- Determine the feasibility of a given set of angle measurements given the properties of parallel lines.
- Explore how changing one angle affects the others.
Real-world Applications

Connect the worksheet to real-life examples:
- Analyze angles created by railroad tracks or architecture.
Example Worksheet Content

Here's a sample layout for your worksheet:
| Problem | Your Answer |
|---|---|
| Given ∠1 = 55°, find the measures of all angles in the diagram. | Draw diagram, calculate and label angles. |
| If ∠5 = 30°, which of these are not true: ∠3 = 30°, ∠6 = 30°, ∠8 = 150°? | Identify and explain. |

📌 Note: Ensure your diagrams are clear and include parallel line markers to distinguish them from others.
After completing the worksheet, students should have a firm grasp on how angles relate to one another when parallel lines are involved.
Summing up, creating a parallel lines transversal worksheet involves setting clear objectives, structuring the worksheet logically, and providing a variety of exercises. This not only aids in the learning process but also fosters a deeper understanding of geometric relationships. By visualizing these principles through worksheets, students engage with the material, leading to better comprehension and retention. Now, armed with this guide, you can craft a worksheet that both educates and entertains, making geometry an accessible and enjoyable subject.
What are the key properties of angles formed by a transversal with parallel lines?

+
The key properties include: corresponding angles are equal, alternate interior and alternate exterior angles are equal, and same side interior angles are supplementary.
Why do we use worksheets for learning parallel lines and transversals?

+
Worksheets provide visual representation, allow practice with calculations, help in identifying angle relationships, and reinforce problem-solving skills in geometry.
How can I make the worksheet more engaging for students?

+
Incorporate real-life scenarios, use color to differentiate angles, add puzzles or fun activities related to geometry, and include challenging questions that promote critical thinking.
What should I do if students struggle with these concepts?

+
Provide additional visual aids, use manipulatives like angle protractors, offer small group sessions for targeted practice, or integrate technology tools like interactive simulations.
Can I use this worksheet for different levels of students?

+
Absolutely. Adjust the complexity of the problems, provide more visual cues for beginners, or introduce abstract thinking and proofs for advanced learners.



