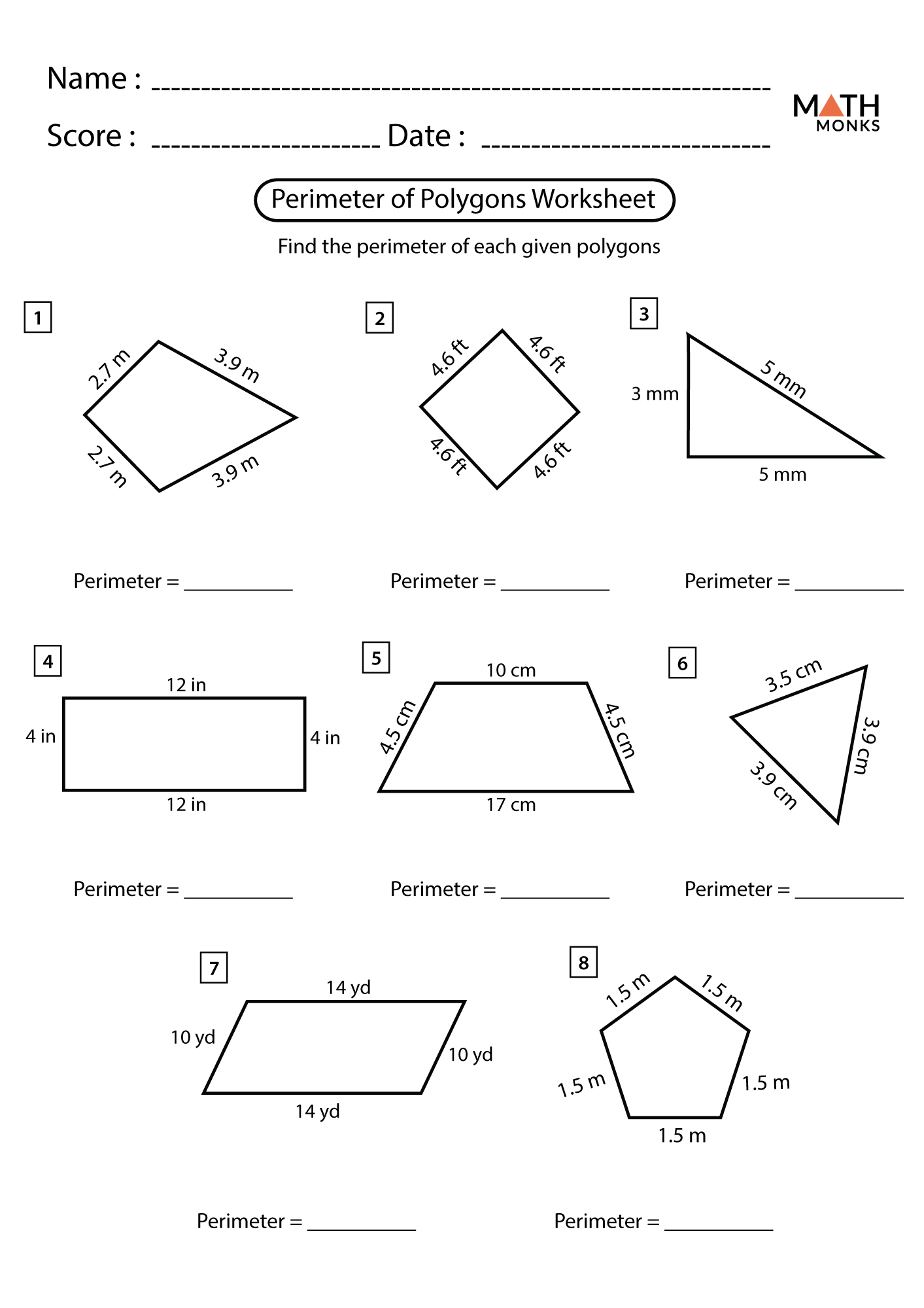
Worksheet 1.1 Answer Key: Points, Lines, Planes Simplified

The study of geometry, particularly in the realm of points, lines, and planes, serves as the fundamental building block for understanding higher concepts in mathematics. Whether you're a student, a teacher, or an enthusiast, grasping these basic elements of Euclidean geometry will provide a clear pathway towards more advanced learning. Let's dive into a comprehensive overview of these elementary shapes, their relationships, and how they interact within space.
Understanding Points

A point in geometry is considered the most fundamental of all geometric objects. Imagine the tip of a pin, the intersection of two lines, or any exact location that you can pinpoint. Here’s what you need to know:
- Points are location without size or shape.
- They are usually denoted by capital letters, like ‘A’, ‘B’, or ‘C’.
- Points do not have length, width, or height; they are dimensionless.
Lines and Their Properties
Lines are one of the most essential concepts in geometry, connecting points in a straight, one-dimensional path:
- A line extends indefinitely in both directions.
- It is often represented by a lowercase letter or the two endpoints.
- Lines can be parallel, intersecting, or collinear.
Planes: The Foundation of Geometry
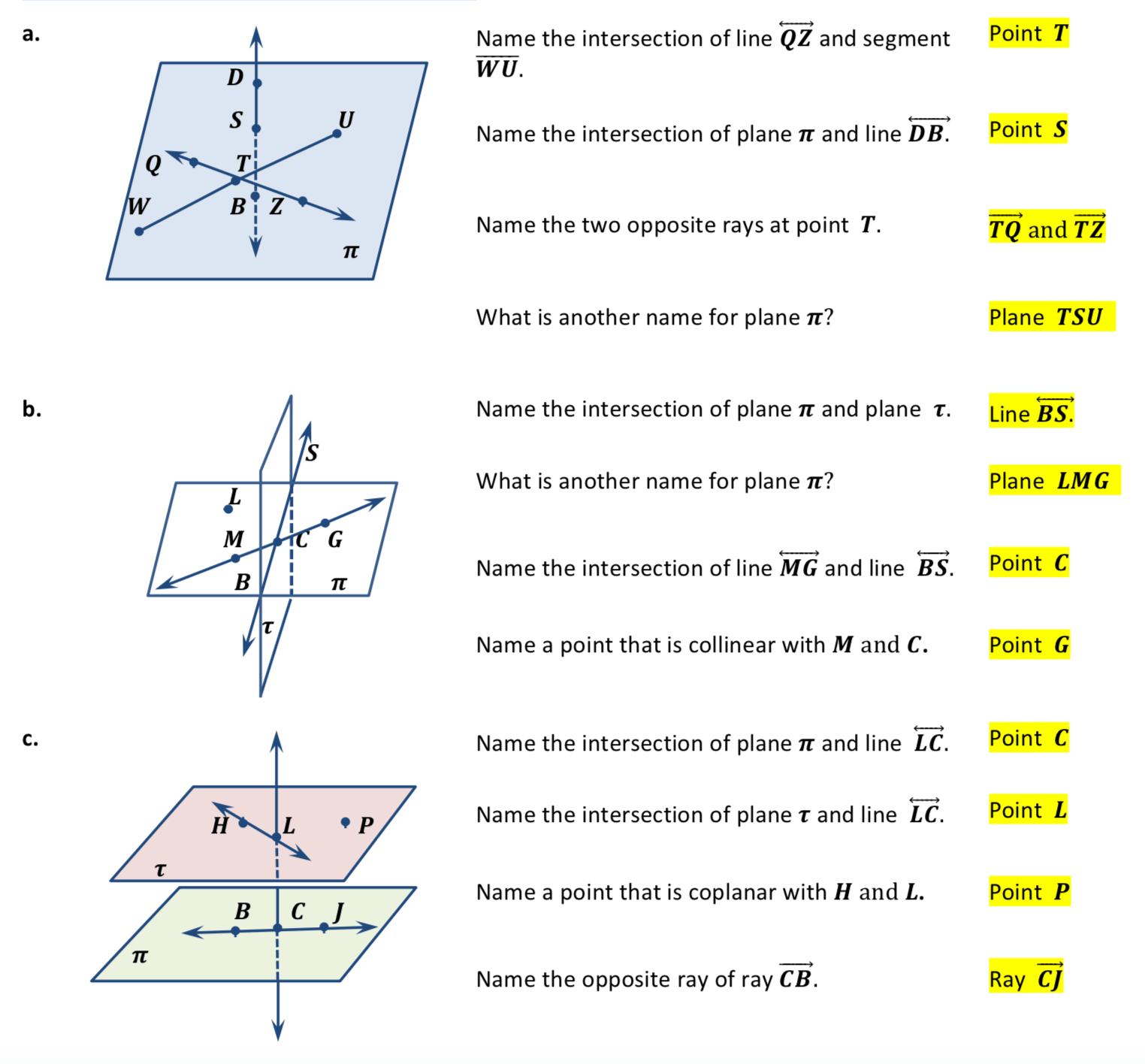
Planes are what can be visualized as flat surfaces that extend infinitely in all directions:
- They are two-dimensional and have no thickness.
- Planes can be named by three non-collinear points or a single uppercase letter.
- Three non-collinear points always determine a unique plane.
Worksheet 1.1 Answer Key

Here’s a summary of the key answers from Worksheet 1.1 to help you understand these basic geometric concepts:
| Question | Answer |
|---|---|
| How many dimensions does a point have? | 0 dimensions |
| What are lines called that never intersect? | Parallel lines |
| Can two planes intersect in more than one point? | No, they intersect in a line. |

Interrelationships Between Points, Lines, and Planes

The interactions between these geometric entities are both fascinating and essential:
- Collinear Points: Points lying on the same line.
- Coplanar Points: Points lying on the same plane.
- Parallel Planes: Planes that never intersect.
- Line-plane Intersection: A line and a plane intersect at a point unless the line lies within the plane or is parallel to it.
Key Points to Remember
Keep these important geometric facts in mind:
- Two points define a unique line.
- Three non-collinear points define a unique plane.
- Two lines can intersect in only one point, be parallel, or coincide.
- A line and a plane can intersect in a line or not at all, depending on their relationship.
As we wrap up, understanding points, lines, and planes is not merely an academic exercise. These basic elements allow us to navigate both physical space and the abstract world of mathematics. From engineering marvels to the simplicity of daily travel, these concepts underpin much of our world. Continue to explore the depth and breadth of geometry; your journey into understanding the world through numbers and shapes has only just begun.
Why is understanding points, lines, and planes important in geometry?
+
These are the basic building blocks of geometry. Without understanding them, it’s challenging to grasp more complex geometric concepts and their applications in real life.
What does it mean for two lines to be parallel?

+
Parallel lines are two lines in the same plane that never intersect or cross each other, even if extended indefinitely.
Can a line intersect a plane in more than one point?
+
If the line is not parallel to the plane, it will intersect the plane at exactly one point. However, if the line lies within the plane, it will intersect at all points on that line.