Inequality Word Problems Worksheet: Solve with Ease

Welcome to our comprehensive guide on solving inequality word problems. Whether you're a student looking to boost your math skills or a teacher aiming to provide engaging content, this guide will walk you through the steps, techniques, and tips to master inequalities in word problems.
Understanding Inequalities

Inequalities are mathematical expressions that describe a range of values rather than a specific value. They use symbols like >, <, ≥, and ≤ to show the relationship between numbers or variables. Here’s a quick rundown:
- >: Greater than
- <: Less than
- ≥: Greater than or equal to
- ≤: Less than or equal to
Step-by-Step Guide to Solving Inequality Word Problems

Let’s dive into how you can approach and solve these problems effectively:
1. Read the Problem Carefully

Always start by reading the problem several times to understand what is being asked:
- Identify the variables (what you’re solving for).
- Recognize the relationships between these variables.
🔍 Note: Pay attention to keywords that signal inequalities like “at least”, “at most”, “no more than”, etc.
2. Write Down the Inequality

Translate the problem into a mathematical inequality:
- Use symbols to represent your variables.
- Formulate the inequality that describes the conditions in the problem.
3. Solve the Inequality
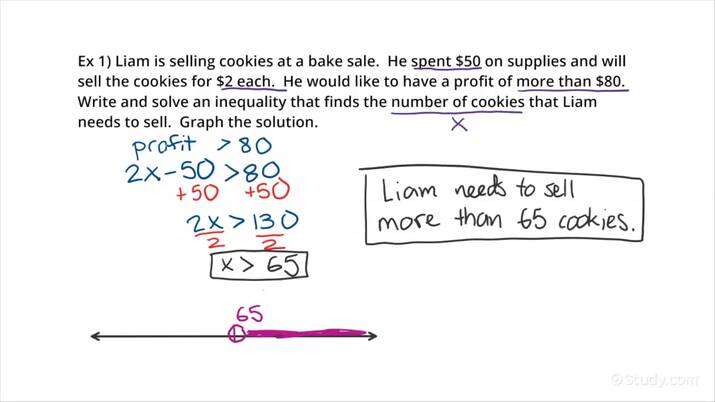
Here are the steps to solve inequalities:
- Isolate the variable: Perform operations to get the variable on one side of the inequality. Remember, if you multiply or divide by a negative number, you must flip the inequality sign.
- Simplify: Reduce both sides to their simplest form.
- Graph the Solution (optional but often required for algebra students): Plot the solution on a number line or use a graphical representation.
4. Interpret the Solution

Once you’ve solved for the variable:
- Check if the solution makes sense in the context of the word problem.
- Remember to include or exclude boundary points as necessary.
5. Verify Your Answer

Substitute your solution back into the original problem to ensure it meets all criteria:
- This step is crucial to avoid common mistakes like not considering the context of the problem.
Examples of Inequality Word Problems

Let’s walk through a couple of examples to illustrate how to apply the steps:
Example 1: The Bakery Problem

A bakery owner wants to spend no more than 150 on flour. If each bag of flour costs 5, how many bags can she buy?
- Translate the Problem: Number of bags (b) × 5 ≤ 150
- Solve: b ≤ 30
- Interpret: The owner can buy at most 30 bags of flour.
Example 2: The Gardening Problem

A gardener has a fence that must be at least 20 feet long. He has already used 10 feet for one side. How long can the other side be?
- Translate the Problem: 10 + x ≥ 20
- Solve: x ≥ 10
- Interpret: The other side of the fence must be at least 10 feet long.
Important Tips for Success
- Understand the problem first: Before diving into math, ensure you comprehend what the question is asking.
- Practice: Like any skill, solving inequalities becomes easier with practice. Use worksheets or online resources to hone your skills.
- Draw a model: Sometimes, visualizing the problem can help in setting up the inequality correctly.
- Know your algebra: Basic algebraic manipulations are key to solving inequalities efficiently.
What are common mistakes when solving inequality word problems?

+
Common mistakes include forgetting to flip the inequality sign when multiplying or dividing by a negative number, misunderstanding the problem context, and neglecting to consider boundary points.
How can I improve my problem-solving skills in math?

+
Regular practice, understanding the theory, breaking problems into smaller steps, and seeking help or tutorials can all enhance your problem-solving skills.
Are there online resources to practice inequality word problems?

+
Yes, several educational websites like Khan Academy, Mathway, and PurpleMath offer exercises and explanations on inequalities and their applications in word problems.
In summary, understanding how to approach inequality word problems involves breaking down the problem, setting up the inequality correctly, solving it, and interpreting the results. With practice, you’ll find these problems not only become manageable but also an intriguing way to apply algebra in real-world scenarios. Whether for academic purposes or personal growth, mastering inequalities can lead to a deeper appreciation and understanding of mathematical logic and reasoning.



