5 Ways to Master Volume of Prisms Worksheet

Mastering the volume of prisms is a fundamental skill for students studying geometry, whether in middle school or beyond. It forms the basis for understanding more complex geometric shapes and their properties. This guide will provide you with five effective strategies to excel in solving volume problems of prisms, using worksheets as a practical tool for reinforcement.
Understanding the Basics

Before diving into the strategies, it's crucial to understand what prisms are and how their volume is calculated. Prisms are polyhedrons with two parallel faces called bases, and all other faces are parallelograms. The volume (V) of any prism can be calculated using the formula:
V = B * h
Where B is the area of the base, and h is the height of the prism (the perpendicular distance between the planes of the two bases). Here are the steps to master the volume:
1. Grasp the Concept of Base Area
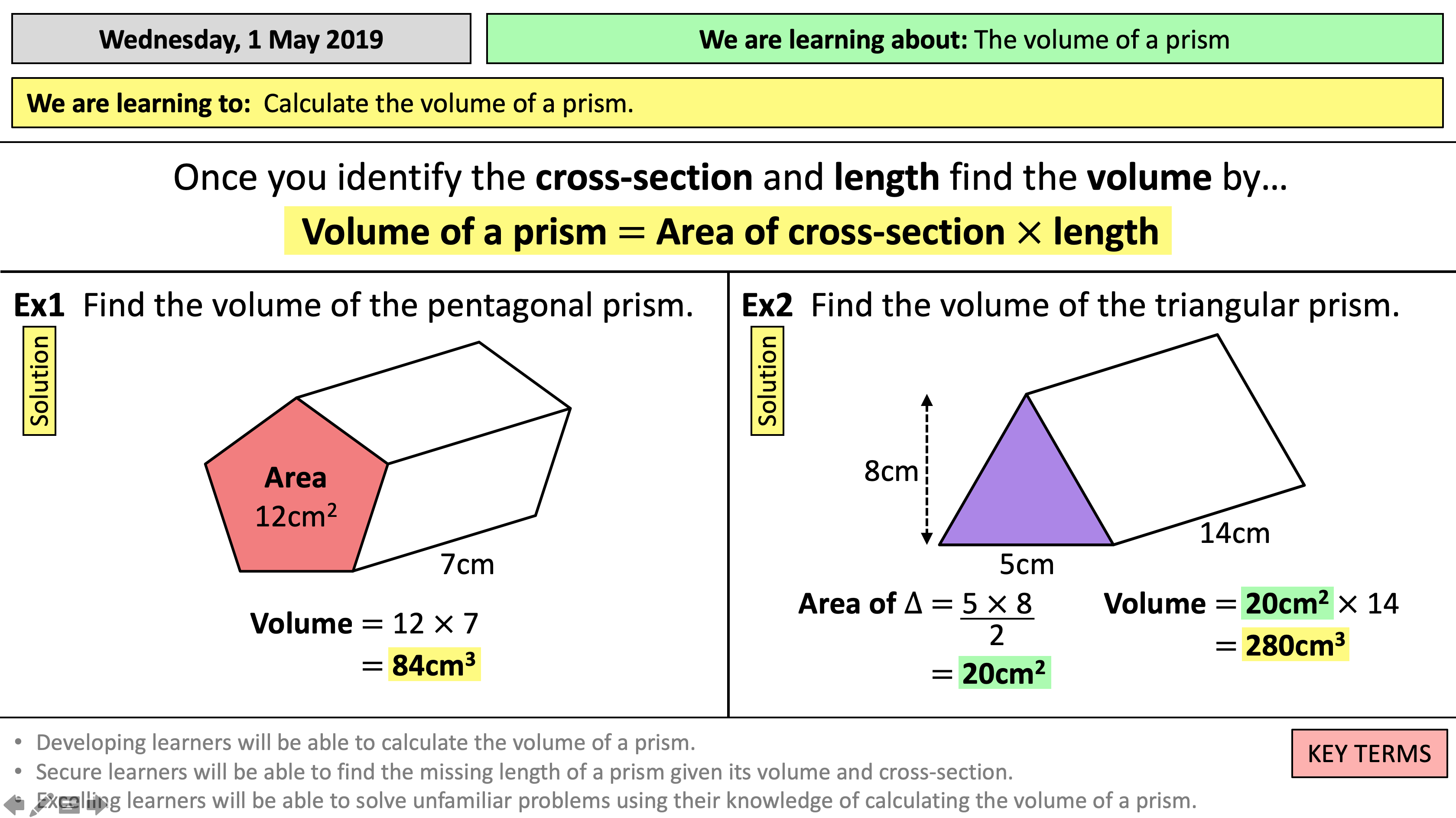
The first step in mastering the volume of prisms involves a solid understanding of base areas. Here are some tips:
- Identify the Shape of the Base: Whether it's a triangle, rectangle, or any other polygon, knowing how to calculate its area is essential.
- Apply Formulas: Use specific formulas for different shapes, e.g., Area of a rectangle = length * width or Area of a triangle = 0.5 * base * height.
📝 Note: Make sure to review the properties of different polygons and their area formulas before tackling the volume worksheet.
2. Use Visual Aids and Diagrams

Visual learning can significantly enhance understanding and retention:
- Draw Prisms: Sketch different prisms, label dimensions, and calculate the volume manually.
- Use Models or Software: Interactive models can provide a 3D visualization, making abstract concepts concrete.
- Color Code: Color-code different parts of the prism to distinguish between height, base, and other dimensions.
3. Practice with Varied Problems
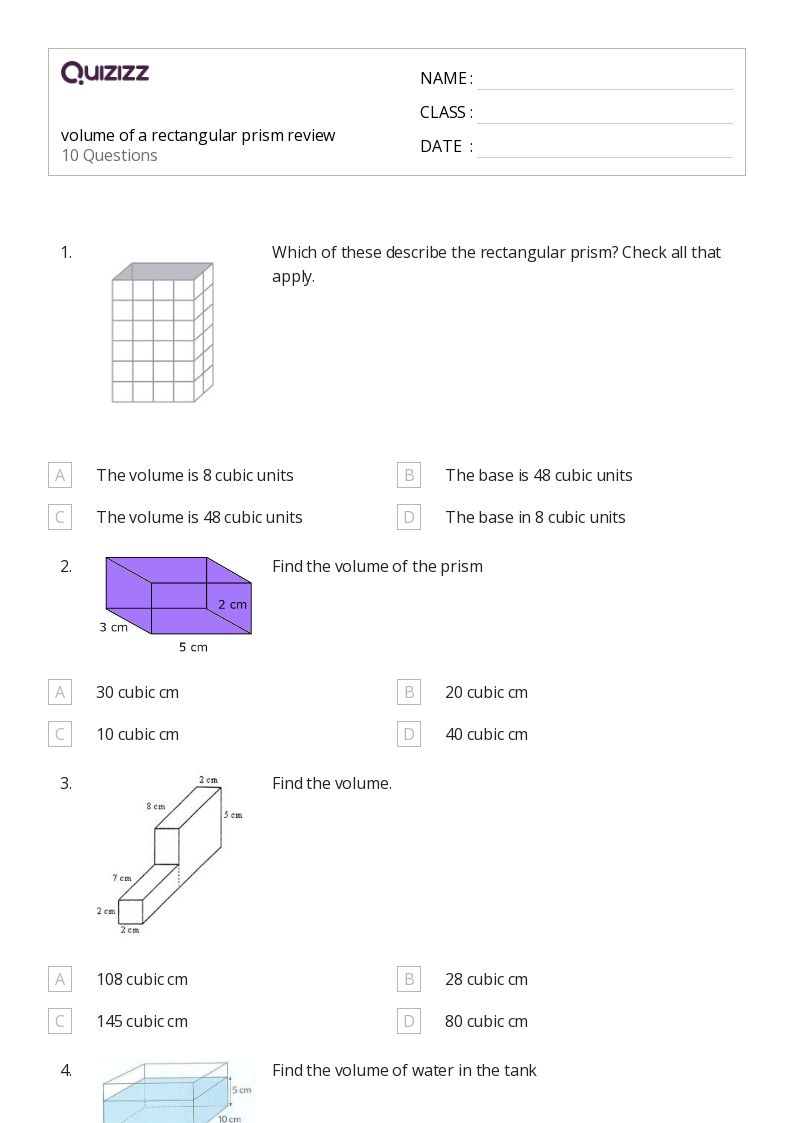
Worksheets can be designed to increase complexity:
- Start Simple: Begin with problems where the base area is given or easily calculated.
- Increase Complexity: Gradually move to problems where the base area needs to be figured out, perhaps with an irregular polygon.
- Real-Life Applications: Include problems that relate volume calculations to real-life scenarios, like how much water a fish tank can hold.
4. Breakdown and Solve Step-by-Step

A structured approach ensures accuracy:
- Identify Known Variables: Clearly note what you know: height, base shape, dimensions of base, etc.
- Calculate Base Area: If not given, calculate the area of the base using the appropriate formula.
- Multiply by Height: Once the base area is known, multiply it by the height of the prism.
- Check Units: Ensure the units are consistent (e.g., cubic centimeters, cubic meters).
📚 Note: Breaking down problems into smaller steps helps in understanding the logic behind volume calculation.
5. Use Worksheets for Reinforcement

Worksheets are an excellent tool for practice:
- Diverse Problems: Ensure your worksheet includes different types of prisms and problem sets that vary in difficulty.
- Gradual Difficulty: Start with easier problems and progressively introduce more challenging ones.
- Self-Evaluation: Include an answer key or evaluation section for students to check their solutions.
| Prism Type | Base Shape | Volume Formula |
|---|---|---|
| Rectangular Prism | Rectangle | V = length * width * height |
| Triangular Prism | Triangle | V = 0.5 * base * height * prism height |
| Hexagonal Prism | Hexagon | V = (3 * √3 * side² / 2) * height |

Incorporating these strategies into your learning or teaching of volume calculations for prisms will lead to a deeper understanding and mastery of the subject. Remember, consistent practice with worksheets, visualization, and real-world applications will solidify your grasp on this geometric concept.
Frequently Asked Questions:
What if the base of the prism isn’t a common polygon?
+
You can break the polygon into triangles and rectangles or look for known formulas for irregular shapes. Alternatively, approximate by simplifying the base to the closest regular polygon and use those area formulas.
How do I handle prisms with slanted or non-perpendicular heights?

+
The volume formula remains the same, but the height you use is the perpendicular distance between the bases, not the slant height. If the height is not given, you might need to use trigonometry or the Pythagorean theorem to find it.
Can the volume of prisms be used for practical applications?

+
Absolutely! From packaging design to construction, understanding volume is crucial. Architects use it to plan space, engineers calculate storage capacity, and chefs might use it for bulk cooking measurements.