5 Easy Ways to Master Volume of Prisms and Pyramids

The volume calculation of prisms and pyramids is a fundamental skill in geometry, essential for both students and professionals in fields like architecture, engineering, and beyond. Today, let's dive into five straightforward techniques to master these calculations, ensuring that you'll be well-versed in determining the volume of these geometric shapes with ease and confidence.
Understanding the Basics

Before we explore the specific methods, let's establish a foundational understanding:
- Prisms have the same cross-section along their entire length.
- Pyramids taper from a base to an apex.
- Volume is measured in cubic units.
💡 Note: Keep in mind that both prisms and pyramids come in various shapes; the formula for volume depends on the base's shape and dimensions.
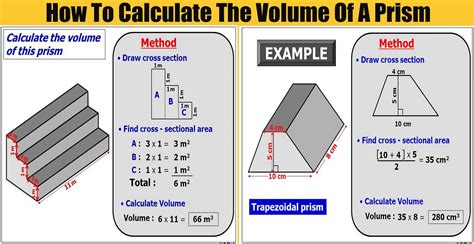
Method 1: Basic Volume Formula

Here’s a straightforward approach:
| Shape | Volume Formula |
|---|---|
| Prisms | Volume = Area of Base × Height |
| Pyramids | Volume = (Area of Base × Height) / 3 |

Let's look at some examples:
- For a rectangular prism, if the base has an area of 12 square units and the height is 5 units, the volume would be 12 × 5 = 60 cubic units.
- For a square pyramid with a base area of 25 square units and a height of 12 units, the volume is (25 × 12) / 3 = 100 cubic units.
Method 2: Using Coordinates

Coordinate geometry can simplify volume calculations. Here’s how:
- Determine the coordinates of the vertices.
- Use the formula for vectors or distances to find the area of the base.
- Calculate the height from one of the base vertices perpendicularly to the apex or opposite side.
🔍 Note: This method can be particularly useful when dealing with complex shapes or when dimensions are provided in coordinates.
Method 3: Cavalieri’s Principle
Based on the principle that prisms or pyramids of equal height with equal cross-sectional areas at all heights have equal volumes:
- Visualize slicing the shapes into infinitesimally thin layers.
- Understand that the sum of these cross-sectional areas equals the volume.
This method is useful for comparing volumes without exact measurements, for instance, if you're dealing with similarly shaped but differently sized objects.
Method 4: Decompose and Conquer

When dealing with irregular shapes, you might:
- Divide the complex shape into simpler prisms or pyramids.
- Calculate the volume of each section separately and then sum these volumes.
📐 Note: This technique is invaluable when dealing with composite figures or when exact dimensions of individual parts are known but not of the whole.
Method 5: Integration and Calculus

For advanced learners or those with an interest in calculus, integrating can be a precise way to find volumes:
- Set up an integral with the area function of the base relative to its height.
- Integrate this function over the height of the prism or pyramid.
📚 Note: While this method involves complex mathematics, it's the gold standard for finding volumes of more intricate or non-standard shapes.
With these five methods in your toolkit, you're now equipped to tackle volume calculations of prisms and pyramids from different angles. Each approach has its strengths, catering to various situations from simple to complex, ensuring you're never stumped by these geometric shapes. Understanding these strategies will not only boost your mathematical skills but also provide practical insights into real-world applications, from calculating the volume of a storage container to designing architectural models.
How do you find the volume of an irregular prism?

+
You can use the decompose and conquer method by breaking down the prism into smaller, regular prisms or pyramids, calculating their volumes separately, and then summing them.
What is the difference between a prism and a pyramid?

+
A prism has two parallel bases of the same shape, and its sides are parallelograms. A pyramid has one base and its sides taper to a single point, known as the apex.
Why do we divide the volume of a pyramid by three?

+
Dividing the volume by three is necessary because a pyramid essentially covers a third of the space a prism of the same base area and height would occupy.