5 Free Volume Cone Worksheet Answer Key Tips
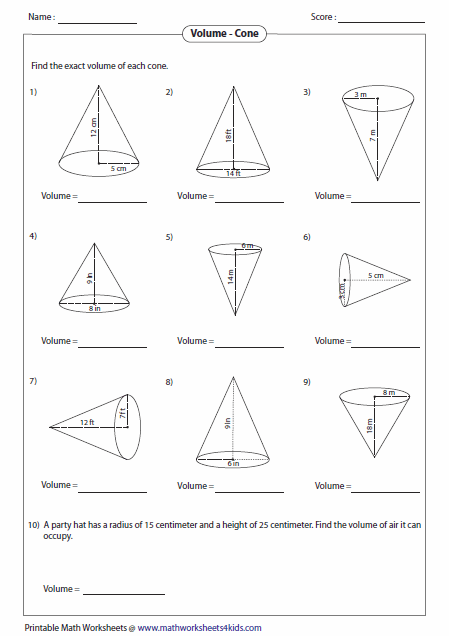
In today's educational landscape, the quest for engaging math exercises that enhance student comprehension is unending. Volume cones offer a unique opportunity to not only delve into the fundamental principles of geometry but also to captivate students with real-world applications. Here, we present five invaluable tips for crafting or utilizing volume cone worksheets with answer keys that promise to transform your teaching approach and enrich the learning experience for your students.
1. Start with the Basics
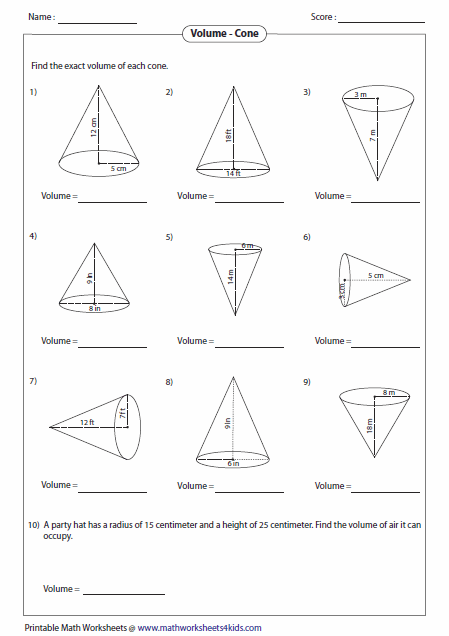
The key to mastering volume cone calculations is a firm grasp of the basics. Before diving into complex problems, ensure your worksheet includes:
- Definitions of volume, base, and height in relation to cones.
- Illustrations demonstrating the three-dimensional structure of a cone.
- Simple word problems that require students to identify and calculate the base radius and height.
- Gradual introduction of the volume formula, showing its derivation from the volume of a cylinder.
🔔 Note: Start with simpler problems to build confidence before introducing more complex scenarios.
2. Incorporate Real-World Scenarios

One of the most effective ways to make mathematical concepts relatable is through real-world application:
- Create problems that involve everyday objects like ice cream cones, traffic cones, or party hats.
- Include situations where students must use problem-solving skills to determine cone dimensions from given volumes or other information.
- Integrate interdisciplinary learning by discussing the applications of cones in architecture, design, and science.
💡 Note: Real-world examples enhance student engagement and help them see the practical utility of geometry.
3. Encourage Visualization and Estimation

Visualizing the cone and estimating its volume is crucial for conceptual understanding:
- Provide diagrams that require students to estimate the cone's volume without exact measurements.
- Ask students to compare the volume of a cone to other geometric shapes like cylinders or pyramids.
- Introduce dynamic software or physical models to give students a tactile experience of changing dimensions and corresponding volume changes.
| Shape | Volume Formula |
|---|---|
| Cone | V = 1/3πr²h |
| Cylinder | V = πr²h |
| Pyramid | V = 1/3Bh |

4. Provide Detailed Explanations in Answer Keys
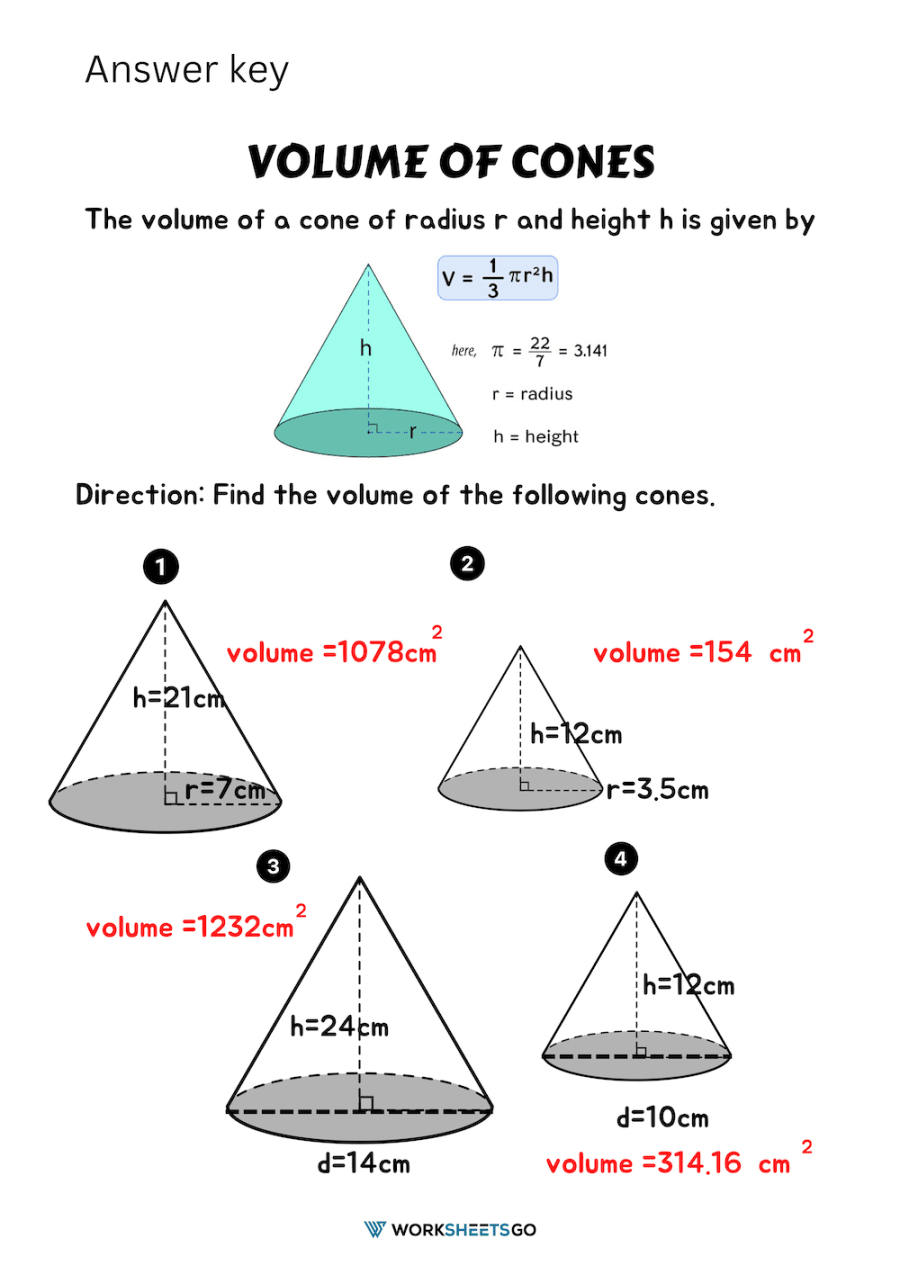
Answer keys should not merely provide the solutions but also the thought process behind them:
- Explain each step in solving the volume calculation problems.
- Include common misconceptions and how to avoid them.
- Offer alternative solutions or methods to encourage students to think flexibly.
- Make use of visual aids like diagrams or graphs to clarify the steps.
📝 Note: Comprehensive explanations help students learn from their mistakes and reinforce correct problem-solving methods.
5. Challenge with Variability

To keep students engaged and push them beyond rote learning, vary your worksheets:
- Introduce variables into problems (e.g., if the height doubles, how does the volume change?)
- Incorporate multi-step problems where students must solve for missing dimensions before calculating volume.
- Encourage critical thinking by asking for comparisons of volumes under different conditions.
📈 Note: The ability to adapt to different problem scenarios helps develop a deeper understanding of volume concepts.
By following these tips, you can craft or utilize volume cone worksheets that are not only educational but also engaging, helping students develop a deep, intuitive understanding of geometric volumes. This approach empowers learners, enhances their problem-solving skills, and makes the study of geometry a more enjoyable journey.
How can I make volume cone problems more interesting for my students?

+
Engage students by embedding the problems within real-life contexts, like comparing the volume of a cone-shaped cup with that of a cylindrical mug, or by including interactive elements like physical models or software simulations.
What common mistakes do students make when calculating the volume of cones?

+
Students often forget to use one-third of the cylinder’s volume formula, confuse the base radius with diameter, or misinterpret slant height as vertical height. Proper guidance and examples can help them avoid these pitfalls.
Can visualization software help with understanding volume?

+
Absolutely. Dynamic software allows students to manipulate the cone’s dimensions in real-time, visualizing how volume changes with different heights, radii, or angles. This can significantly enhance spatial understanding and conceptual learning.
Why is real-world application important in teaching volume concepts?

+
Connecting abstract math concepts to real-world scenarios helps students see the relevance of what they’re learning, increases motivation, and improves their ability to apply mathematical principles practically.
How can I ensure students aren’t just memorizing formulas?
+
Vary the problem types, introduce conditions where they must derive the formula or estimate based on visualization, and emphasize understanding over memorization by encouraging creative problem-solving.