7 Simple Steps to Master Prism Volumes and Areas

Learning to calculate volumes and surface areas using prisms might seem daunting, but with the right approach, you can master these essential mathematical concepts. Here are seven straightforward steps to help you understand and apply prism calculations effectively.
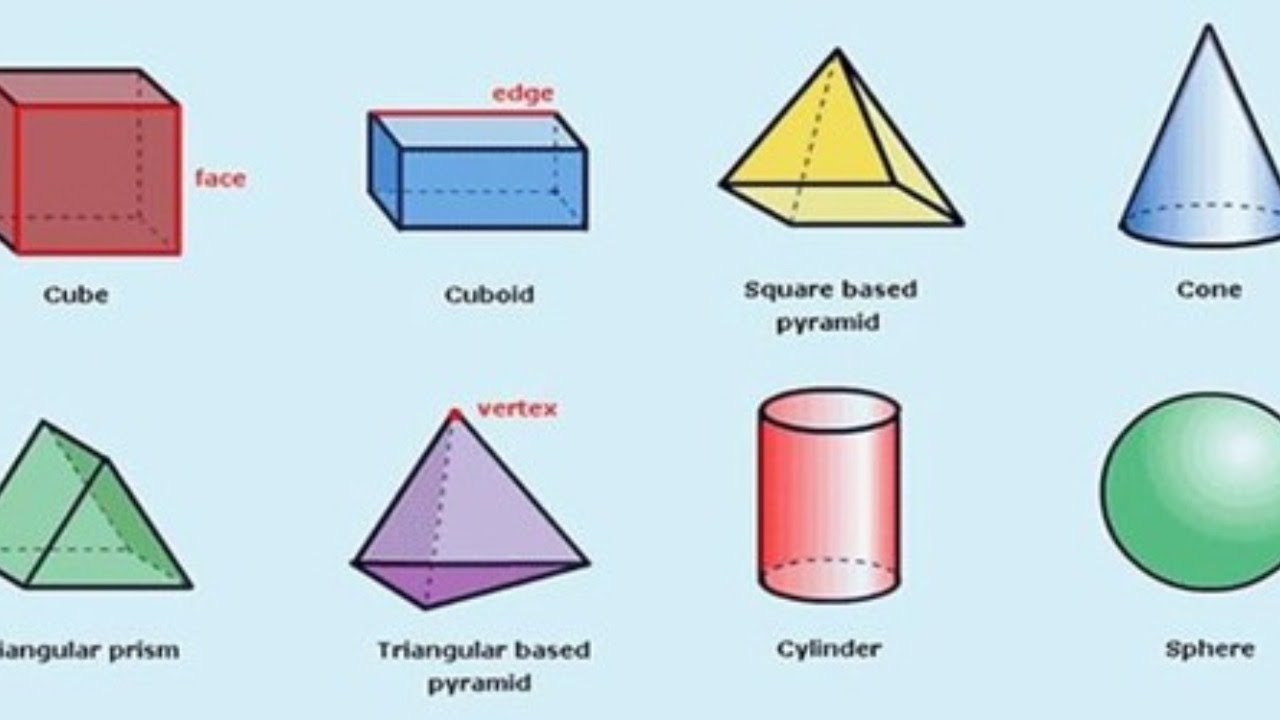
Understanding the Basics of Prisms


To master prisms, one first needs to understand their basic structure. A prism is a three-dimensional shape with two identical parallel bases, which can be any polygon. The most common type, a rectangular prism, has rectangular bases, while a triangular prism has triangular bases. Here are some fundamental points:
- The shape of the base determines the type of prism.
- Height is the perpendicular distance between the bases.
- The volume is derived from the area of the base multiplied by the height.
- Surface area includes the areas of all the faces, including the bases and the lateral faces.
Step 1: Identify the Type of Prism

Recognizing the type of prism is crucial for your calculations. You need to:
- Determine the shape of the base (rectangle, triangle, hexagon, etc.).
- Identify the number of sides in the base for prisms with regular polygons as bases.
Step 2: Calculate the Base Area
The first step in calculating the volume and surface area of a prism is to find the area of the base. Here are examples:
- For a rectangular prism: Base Area = Length × Width
- For a triangular prism: Base Area = (1⁄2) × Base × Height
- For a hexagonal prism: Base Area = 3 × √3/2 × Side2
💡 Note: Always double-check your base area calculations, as errors here will affect all subsequent steps.
Step 3: Determine the Height

Measure the height of the prism, which is the perpendicular distance between the two bases:
- For straight prisms, this is straightforward.
- Oblique prisms require calculating the perpendicular height from one base to the other, not just the straight-line distance.
Step 4: Calculate the Volume
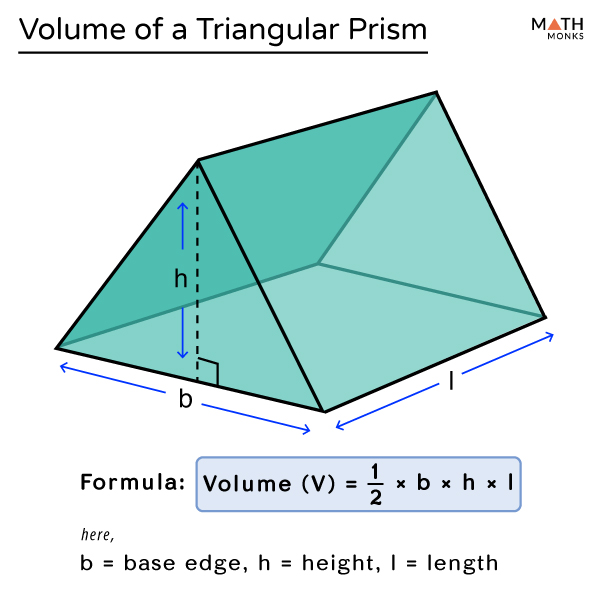
Once you have the base area and the height, calculate the volume using the formula:
Volume = Base Area × Height
Here are some examples:
- Rectangular Prism: V = (Length × Width) × Height
- Triangular Prism: V = ((1⁄2) × Base × Height) × Prism Height
Step 5: Calculate the Lateral Surface Area

The lateral surface area includes all the side faces except the bases:
- For a rectangular prism: Lateral Surface Area = 2 × (Length × Height) + 2 × (Width × Height)
- For a triangular prism: The sum of the areas of three rectangles, each with a base as one side of the triangle.
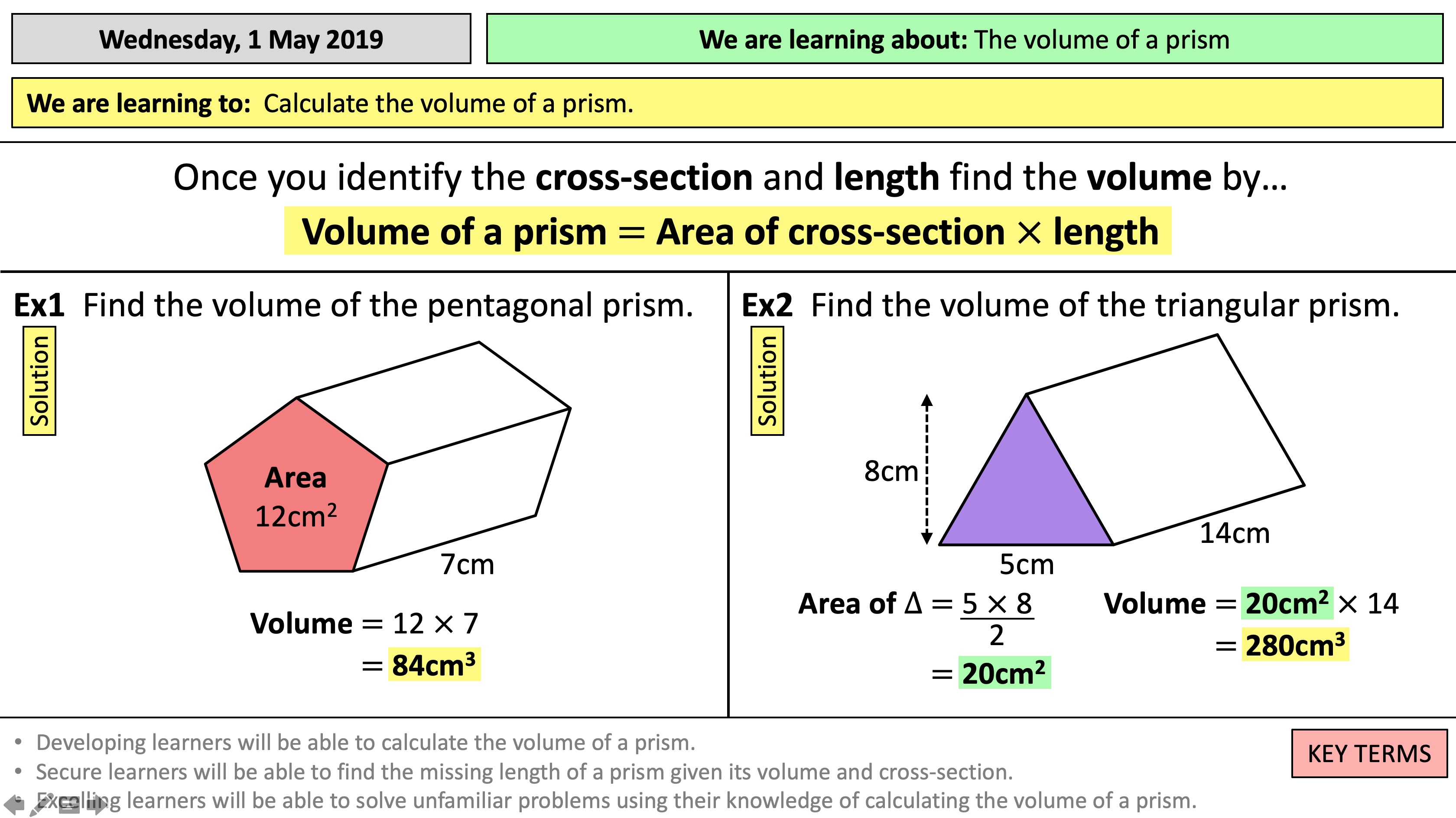
Step 6: Calculate the Total Surface Area
To find the total surface area, add the areas of the two bases to the lateral surface area:
- Total Surface Area = 2 × Base Area + Lateral Surface Area
Step 7: Practice and Apply
Finally, the only way to master prism volumes and areas is through practice:
- Use real-world scenarios where prisms are prevalent, like boxes, swimming pools, or even architectural structures.
- Solve a variety of problems that involve different types of prisms.
By following these steps and regularly practicing, you'll develop a strong understanding of prisms. This knowledge not only enhances your mathematical skills but also helps in various applications, from calculating material needs for construction to understanding geometric shapes in design and engineering.
Understanding these concepts ensures that you're well-equipped to handle practical problems where volumes and areas are crucial. Whether you're studying for an exam, tackling a project, or simply satisfying your curiosity, mastering prisms provides you with a solid foundation in spatial reasoning and problem-solving.
What are the common mistakes when calculating prism volumes?

+
Common mistakes include miscalculating the base area, confusing the height of the prism with the height of the triangular base in triangular prisms, and omitting one or both bases when calculating total surface area.
How does changing the shape of the base affect the volume?

+
Changing the shape of the base impacts the volume by altering the base area. A larger base area results in a larger volume, given the same height of the prism.
Can prisms have curved faces?

+
No, prisms by definition have flat polygonal faces. Shapes with curved faces are referred to as cylinders or other types of three-dimensional figures.



