Venn Diagram Probability Practice: Fun and Simple Worksheets

Understanding probabilities using Venn diagrams can not only be an educational journey but also an entertaining one. Venn diagrams, with their overlapping circles, provide a visual representation of sets and their relationships, making the concept of probability more intuitive and accessible. Here, we'll dive into how Venn diagrams can simplify probability calculations and offer you some practice worksheets to test your understanding.
What Are Venn Diagrams?

Venn diagrams are graphical illustrations used to depict logical relationships between different groups of items, often using overlapping circles. Each circle represents a set, and the overlapping areas represent the intersection or common elements between sets. Here’s how they work:
- Set Representation: Each circle in a Venn diagram represents a set of items. For example, if you’re comparing two groups of students who play either soccer or basketball, one circle might represent soccer players, and another basketball players.
- Intersections: The area where the circles overlap shows items that belong to both sets. In our example, this area would be for students who play both soccer and basketball.
- Complement: The area outside the circles represents elements not in either set.
Probability with Venn Diagrams
Calculating probabilities with Venn diagrams involves understanding how elements are distributed across the sets. Here’s a step-by-step guide:
- Identify Total Elements: Know the total number of items in your sample space.
- Assign Elements: Assign numbers or proportions to each section of the Venn diagram based on the data given.
- Calculate Individual Probabilities: Determine the probability of an event by dividing the number of elements in a specific region by the total number of elements.
- Calculate Combined Probabilities: Use rules like union or intersection to find the probability of combined events.
Practice Worksheets for Probability with Venn Diagrams

To solidify your understanding, here are some worksheets you can use:
| Worksheet Name | Description |
| Basic Venn Probability | Simple set-ups with two or three overlapping sets where students calculate probabilities for individual or combined events. |
| Conditional Probability | Worksheets focused on understanding and calculating conditional probabilities based on given Venn diagrams. |
| Bayes’ Theorem | Practice applying Bayes’ theorem using Venn diagrams to update probabilities based on new information. |

Steps to Use Venn Diagrams for Probability
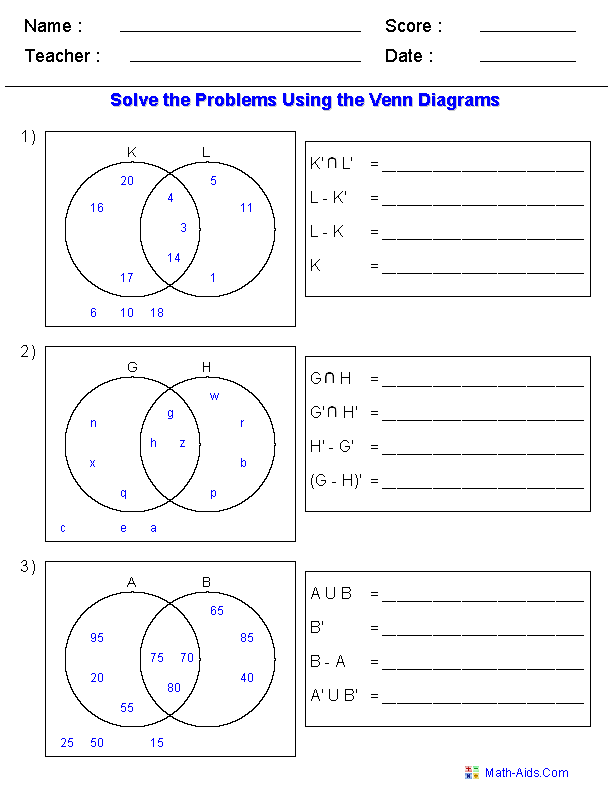
Here’s how you can effectively use Venn diagrams for probability calculations:
- Draw the Diagram: Start by drawing the Venn diagram with circles representing sets. Label each circle clearly.
- Assign Numbers: Based on the problem, assign numbers to the different sections of the Venn diagram, including intersections.
- Use Formulas: Use formulas for probability:
- Probability of an event (A) = Number of elements in (A) / Total elements
- Union probability: (P(A \cup B) = P(A) + P(B) - P(A \cap B))
- Intersection probability: (P(A \cap B) =) Elements in intersection / Total elements
- Check Consistency: Ensure your assigned numbers make sense in the context of the whole diagram (total elements match, etc.).
- Calculate: Perform the calculations step-by-step.
⚠️ Note: Always verify your calculations by summing up the probabilities to ensure they equal one, considering all possible outcomes.
By practicing these worksheets, you'll not only improve your probability skills but also enhance your logical thinking through visual aids like Venn diagrams. These tools can be particularly useful in real-world applications where data sets overlap or where you need to consider multiple events simultaneously.
Why are Venn diagrams useful for calculating probabilities?

+
Venn diagrams visually represent the relationships between sets, making it easier to understand and calculate probabilities by showing where elements overlap or exist exclusively in one set. They simplify complex probability problems by breaking them down into simpler, visual components.
How can I verify my probability calculations?

+
To verify your calculations, sum the probabilities of all disjoint events, which should equal one if done correctly. Also, check for consistency in the Venn diagram; total numbers should add up to the sample space provided.
What common mistakes should I avoid when using Venn diagrams for probability?

+
Avoid these common errors:
- Forgetting to account for elements in intersections when calculating probabilities.
- Not summing up probabilities of mutually exclusive events to check if they equal one.
- Incorrectly assigning elements to regions or using incorrect formulas for probability calculations.
In summary, Venn diagrams are a powerful tool for understanding and calculating probabilities. Through visual representation, they simplify the concepts of sets and logical relationships, making it easier to grasp the principles of probability. The worksheets provided offer a fun way to practice and refine these skills. As you delve deeper into the practice, remember that every probability problem is a logical puzzle waiting to be solved with clarity and precision, making your journey in probability both rewarding and engaging.



