Vector Voyage Worksheet 2: Mastering Vector Basics

Welcome aboard the thrilling expedition of mastering vector basics with Vector Voyage Worksheet 2. As we delve into the intricacies of vectors, this comprehensive guide will be your compass, navigating you through definitions, essential operations, and real-life applications of vectors. From the basic understanding of vectors as arrows in space to how they influence our daily lives through physics and technology, we're here to explore every dimension of this fascinating concept.
Understanding Vectors

Vectors are an integral part of mathematics, physics, engineering, and computer graphics, to name just a few areas. They are quantities with both magnitude (or length) and direction, contrasting with scalars which only have magnitude. Here’s what you need to know:
- Direction: Vectors have an orientation in space, often represented by an arrow.
- Magnitude: The length of the vector arrow represents the magnitude, which can be calculated using the Pythagorean theorem in a Cartesian coordinate system.
- Types: Vectors can be position vectors, velocity vectors, acceleration vectors, etc., depending on what they describe.
Visualizing Vectors

Let’s visualize a vector in a 2D coordinate system:
| Vector | Coordinates (x, y) | Magnitude | Direction |
|---|---|---|---|
 |
(3, 4) | 5 | 53.13° above x-axis |
 |
(-1, -2) | √5 ≈ 2.236 | 296.56° above x-axis |

⚠️ Note: The magnitude of a vector (v) is calculated as |v| = √(x² + y²), where x and y are the coordinates.
Vector Operations

Vectors allow for a variety of mathematical operations, enabling us to perform complex calculations and analyses in diverse fields. Let’s explore these operations:
Vector Addition

Vector addition involves placing vectors head to tail and drawing the resultant vector from the tail of the first vector to the head of the last. Here’s how:
- Choose a reference point for the origin.
- Place the tail of the first vector at the origin.
- Add the second vector by placing its tail at the head of the first.
- Continue this process for all vectors involved.
- The resultant vector is drawn from the origin to the last vector’s head.
Vector Subtraction

Vector subtraction can be thought of as the addition of a negative vector. To subtract Vector B from Vector A:
- Change Vector B to -B by reversing its direction.
- Add -B to Vector A, following the vector addition rules.
Scalar Multiplication

Multiplying a vector by a scalar changes its magnitude, but not its direction. Here’s the process:
- If the scalar is positive, the vector’s direction remains unchanged.
- If the scalar is negative, the vector’s direction is reversed.
- The magnitude of the resultant vector is the product of the scalar and the original vector’s magnitude.
Real-Life Applications of Vectors

Vectors have a tangible impact on numerous fields. Here are some real-world applications:
Physics

In physics, vectors are used to describe:
- Force: Represented by force vectors, describing both the magnitude (how strong) and direction.
- Velocity: Velocity vectors define an object’s speed and direction of movement.
- Acceleration: Similarly, acceleration vectors describe how velocity changes in direction and magnitude.
Computer Graphics

In computer graphics, vectors play a crucial role:
- Positioning and Movement: Vectors are used to move, scale, and rotate 2D and 3D objects on a screen.
- Lighting and Shading: They help calculate lighting effects by determining the direction of light sources relative to object surfaces.
- Ray Tracing: Ray tracing uses vectors to model how light interacts with scenes, determining reflections, refractions, and shadows.
Navigation
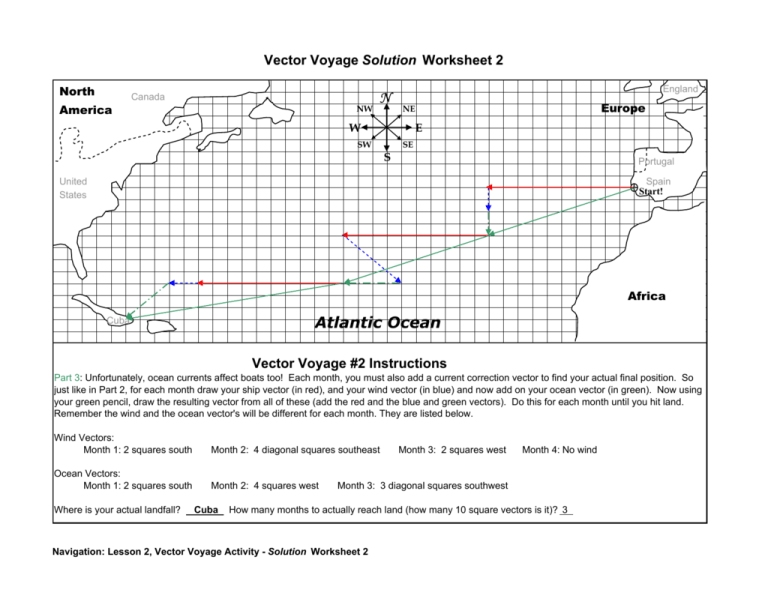
Navigation systems leverage vectors to:
- Calculate displacement, where vectors point from one location to another.
- Plot trajectories, like those used in GPS systems for routing and travel predictions.
- Provide thrust vectors in aerospace engineering to control the movement of aircraft and spacecraft.
🌐 Note: Applications of vectors aren't limited to these fields; they're also critical in engineering, robotics, and many other technological disciplines.
Further Exploration and Worksheets

If you’ve developed a keen interest in vectors, here are some worksheets to practice:
- Worksheet 1: Basic Vector Addition and Scalar Multiplication.
- Worksheet 2: Vector Subtraction and Negative Vectors.
- Worksheet 3: Applying Vectors in Physics Problems.
- Worksheet 4: Vector Applications in Computer Graphics.
Each worksheet progressively challenges you with real-world scenarios that utilize vectors.
In recapitulation, mastering vectors opens up a world of possibilities where you can navigate through spatial problems with ease. Vectors are not merely theoretical constructs but tools that you can employ to solve practical problems in numerous disciplines. Whether you're charting a course for a spacecraft, designing a new video game, or understanding the forces at play in a bridge, vectors are your silent navigators. Embrace the journey through vector space, and you'll find yourself equipped with a powerful mathematical toolset ready to tackle real-world applications and beyond.
Why are vectors important in computer graphics?

+
Vectors are crucial in computer graphics for manipulating objects in 3D space, calculating lighting effects, and simulating physics-based interactions. They help in creating realistic visual environments by handling positioning, scaling, rotation, and much more.
How do you determine the magnitude of a vector?

+
The magnitude of a vector is determined using the Pythagorean theorem. For a vector with components (x, y, z) in 3D space, the magnitude |v| is calculated as |v| = √(x² + y² + z²). In 2D, it simplifies to |v| = √(x² + y²).
Can vectors help with navigation systems?

+
Absolutely! Vectors are fundamental in navigation for calculating displacement, determining trajectories, and managing the direction of travel. GPS systems and flight path calculations use vectors to guide us from point A to point B efficiently.