Mastering Variables on Both Sides: Worksheet Guide

Algebraic equations can be quite challenging for many students, but once you understand the fundamentals, it becomes a lot easier. One critical aspect students often find tricky is solving equations where variables appear on both sides. This guide aims to help you master the process of solving equations with variables on both sides through a structured worksheet approach. By the end of this blog post, you'll be well-equipped with the knowledge and techniques needed to tackle such problems effortlessly.
Understanding Variables on Both Sides

Before diving into the worksheet, it's essential to understand why variables might appear on both sides of an equation. Variables on both sides often arise in problems where you are comparing two quantities or situations where an initial condition has evolved over time, or in physics where two opposing forces are balanced. Here are some key points:
- Equations can be thought of as a balance scale; what you do to one side, you must do to the other.
- Variables on both sides mean you have to isolate the variable on one side to solve for it.

Step-by-Step Guide to Solving Equations with Variables on Both Sides

Here’s how to approach solving equations where variables appear on both sides:
1. Simplify Both Sides of the Equation

- Distribute or combine like terms to simplify each side.
- Remove any parentheses by applying the distributive property.
2. Move Variables to One Side
- Decide which side you want your variable on, typically the left side.
- Move all the variable terms to this side by adding or subtracting terms.
3. Isolate the Variable

- Perform necessary operations to isolate the variable (multiply or divide).
- Remember to do these operations on both sides of the equation to maintain balance.
4. Solve for the Variable

- After isolating the variable, perform the final operation to solve for it.
5. Check Your Solution

- Substitute your solution back into the original equation to ensure it balances.
Here is an example:
x + 1 = 2x - 5
1 = x - 5
6 = x
💡 Note: Ensure all like terms are combined before proceeding to step 2.
Common Pitfalls and How to Avoid Them

Solving equations with variables on both sides isn’t without its challenges. Here are some common mistakes and how to avoid them:
- Misinterpreting Signs: Be careful with negative signs, especially when distributing or combining terms.
- Mixing Steps: Keep each step distinct. Don’t combine multiple operations at once; it increases the risk of errors.
- Forgetting to Distribute: Always distribute constants to all terms within parentheses.
- Incorrect Isolation: Ensure you isolate the variable correctly by applying the correct operations on both sides.
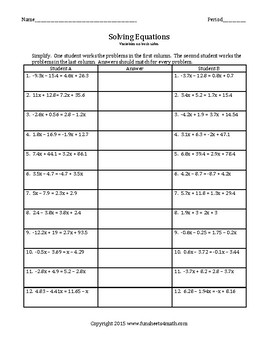
Worksheet to Practice
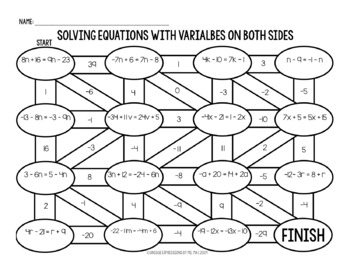
To help you master these skills, here is a worksheet tailored to give you varied practice in solving equations with variables on both sides:
| Equation | Steps | Solution |
|---|---|---|
| 2x + 3 = x + 1 | Step 1: Simplify both sides. Step 2: Move x to one side. Step 3: Isolate x. | x = -2 |
| 4x + 5 = 9 - 2x | Step 1: Combine like terms. Step 2: Move 4x to the left. Step 3: Solve for x. | x = 2 |
| 3(x - 1) = 2(x + 2) | Step 1: Distribute. Step 2: Move variables to one side. Step 3: Isolate x. | x = 5 |

Try solving these examples on your own. Remember, the key is practice and understanding each step thoroughly.
As you work through this worksheet, you'll find that the process of solving equations with variables on both sides becomes second nature. Remember, the goal is not just to find the solution but to understand the process, anticipate common errors, and develop problem-solving strategies.
By mastering this fundamental algebraic technique, you'll find solving equations and tackling more complex problems easier. With consistent practice, you'll be well on your way to becoming an algebra pro, capable of handling equations with variables on both sides with confidence and skill.
Why are variables on both sides of an equation?

+
Variables can appear on both sides due to real-life scenarios where you’re comparing or balancing two quantities or when initial conditions evolve over time.
What’s the first step when solving equations with variables on both sides?

+
The first step is to simplify both sides of the equation by distributing or combining like terms.
How can I avoid common errors when solving such equations?

+
Be cautious with sign changes, keep steps separate, ensure distribution, and isolate the variable correctly on both sides.


