5 Must-Know Unit Circle Tips with Worksheet Answers

The unit circle is one of the foundational tools in trigonometry, essential for understanding angles, trigonometric functions, and their applications in calculus and real-world problems. Here, we'll explore five crucial tips to master the unit circle, along with a worksheet to test your understanding. Whether you're a student struggling with trigonometry or someone looking to brush up on your math skills, these insights will help make the unit circle less intimidating.
1. Understand the Basics of the Unit Circle


Before delving deeper, it’s imperative to grasp what the unit circle represents:
- Radius: The distance from the center to any point on the circle is always 1.
- Angles: Typically measured in radians, but degrees are also commonly used. A full rotation around the circle is 360 degrees or 2π radians.
- Coordinate System: Each point on the circle can be described by coordinates (x, y), where x and y are the cosine and sine of the angle, respectively.
✏️ Note: Understanding the layout of the circle and the significance of different angles (such as 0°, 90°, 180°, 270°) can dramatically simplify complex trigonometric problems.
2. Learn the Key Angles and Their Coordinates
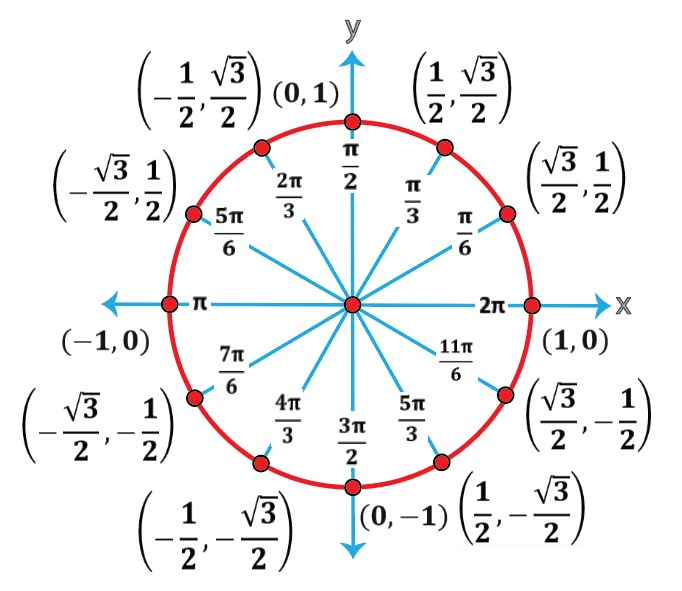

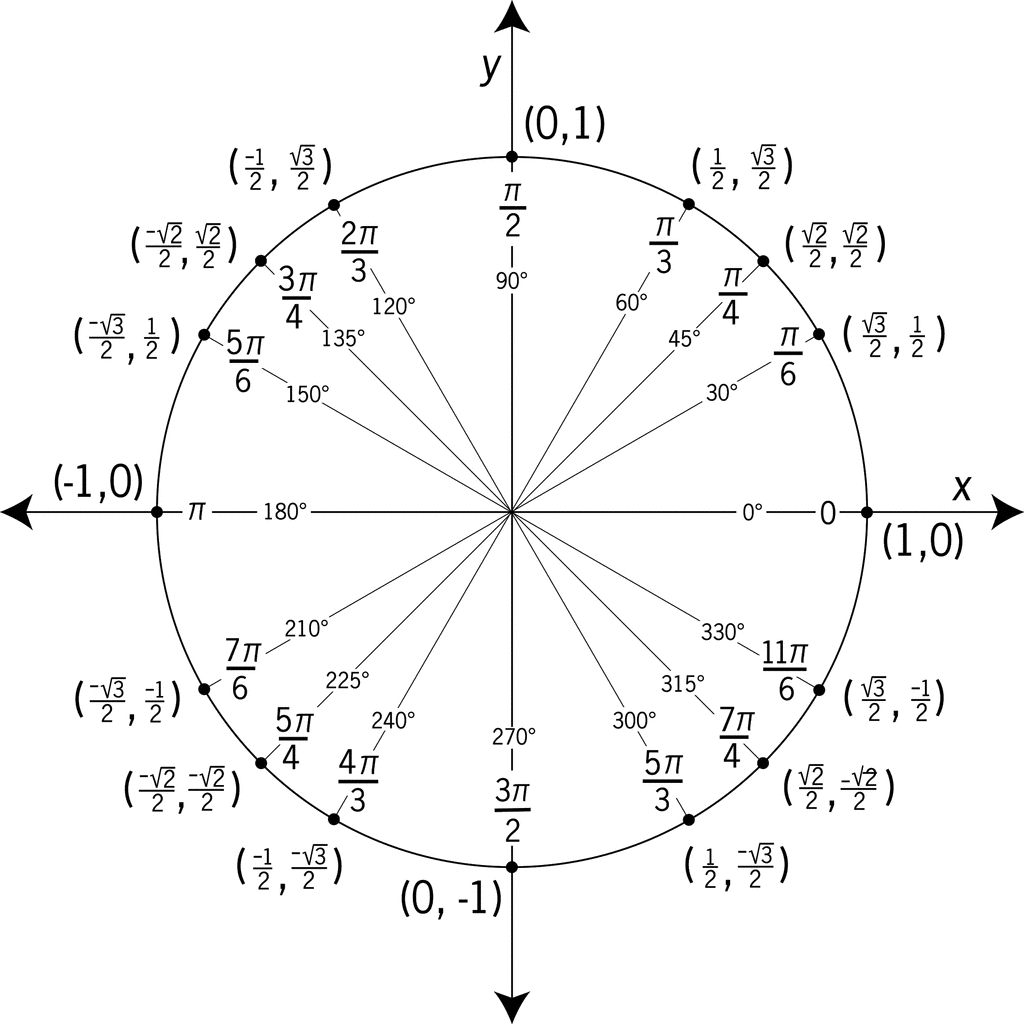
Memorizing or understanding the coordinates for common angles can save you time:
- 0° (or 360°): (1, 0)
- 90° (or π/2 radians): (0, 1)
- 180° (or π radians): (-1, 0)
- 270° (or 3π/2 radians): (0, -1)
- 45° (or π/4 radians), 135° (or 3π/4), 225° (or 5π/4), 315° (or 7π/4): Use the Pythagorean identity (sin²θ + cos²θ = 1) to find coordinates like (±√2/2, ±√2/2).
3. Relate Trigonometric Functions to the Unit Circle
| Function | Expression on Unit Circle |
|---|---|
| sine | y-coordinate |
| cosine | x-coordinate |
| tangent | y/x (but be aware of undefined points) |

Every trigonometric function can be directly related to the coordinates on the unit circle, providing a visual tool to understand their periodicity, amplitude, and phase shifts:
- As θ increases from 0° to 360°, sine and cosine complete one cycle, oscillating between -1 and 1.
- Tangent is only defined when the x-coordinate isn’t zero, which explains why it has vertical asymptotes at multiples of π/2.
✏️ Note: Visualizing functions on the unit circle helps in solving problems involving phase shifts and periodic behavior in trigonometry.
4. Use Symmetry and Symmetry Reduction


The unit circle is symmetrical across multiple axes:
- Horizontal symmetry: sin(θ) = sin(π - θ) and cos(θ) = -cos(π - θ).
- Vertical symmetry: sin(θ) = -sin(-θ) and cos(θ) = cos(-θ).
- Quarter circle symmetry: Values repeat with a phase shift of 90°, like sin(θ) = cos(θ - π/2).
These properties can simplify calculations significantly:
- If you know sin(30°) = 1⁄2, then sin(150°) = 1⁄2, and sin(-150°) = -1⁄2, and so on.
5. Practice with a Worksheet

Here’s a worksheet to help you solidify your understanding:
- Find the exact value of cos(3π/4).
- Determine the quadrant in which θ = 240° is located.
- Calculate sin(π/6).
- What are the coordinates for θ = -5π/6?
- Given that tan(θ) = -1, find θ in degrees where θ ranges from 0 to 360.
Now, let's delve into summarizing the key points from our exploration of the unit circle.
The unit circle is a powerhouse in trigonometry, aiding in solving problems, understanding functions, and visualizing relationships. Mastering it requires recognizing the basics, knowing key angles, relating trigonometric functions to the circle's coordinates, using symmetries, and practicing with problems. These tips provide a solid foundation to approach trigonometric problems with confidence. Remember, repetition and visualization will make these concepts second nature, enhancing your mathematical prowess not just in trigonometry but also in calculus and beyond.
What is the difference between radians and degrees?

+
Degrees measure angles as parts of a 360-degree full circle, whereas radians measure angles in terms of the radius of the circle. A full circle is 2π radians.
Why is the unit circle important in trigonometry?

+
The unit circle helps in understanding the properties and relationships of trigonometric functions, making it easier to solve problems, graph functions, and comprehend periodicity.
Can the unit circle be used for complex numbers?

+
Yes, the unit circle can be extended to represent complex numbers, where the x-axis represents the real part and the y-axis the imaginary part, especially useful in the study of Euler’s formula.