Right Triangles and Trigonometry Answers: Master Unit 8 Easily
Exploring the world of geometry can be a fascinating journey, especially when we delve into topics like right triangles and trigonometry. For many students, Unit 8 on these subjects can pose a considerable challenge. Yet, with the right understanding and methods, you can not only overcome the difficulty but also excel in this mathematical field. This blog post aims to provide you with an in-depth exploration of right triangles, trigonometry, and how to master the answers in Unit 8 effortlessly.
Understanding Right Triangles
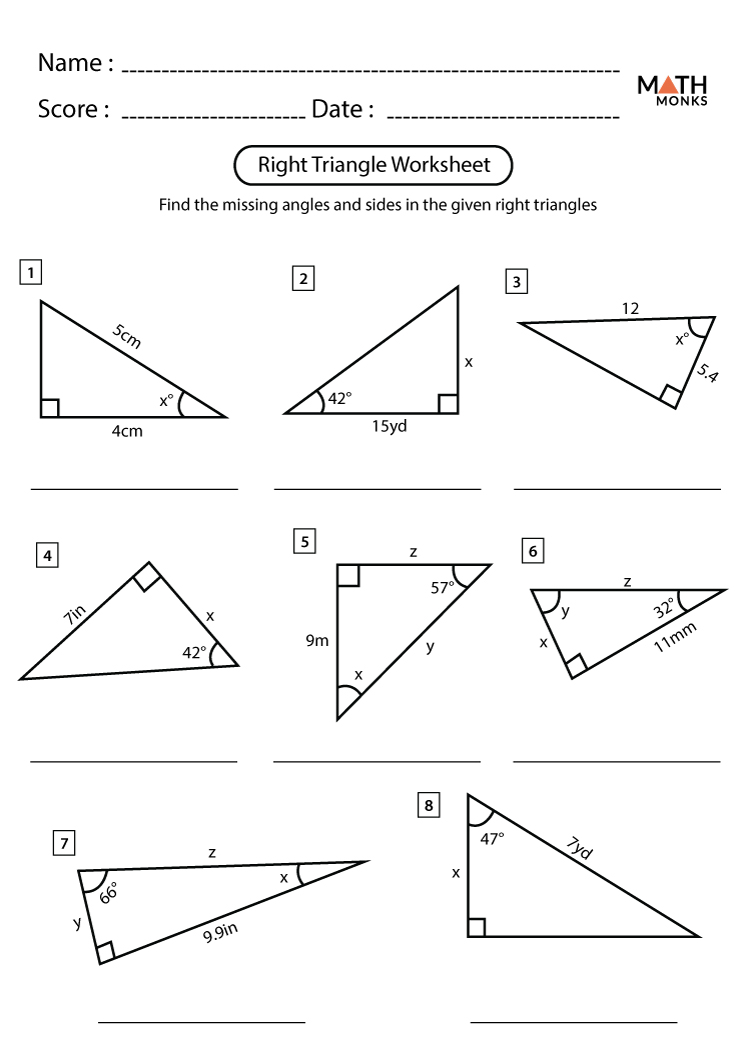
A right triangle, by definition, contains one angle measuring 90 degrees. The sides of a right triangle have special names:
- Hypotenuse - the longest side, which is opposite to the right angle.
- Leg - either of the other two sides.
Understanding the Pythagorean Theorem is crucial:
a2 + b2 = c2, where a and b are the legs, and c is the hypotenuse.
🔍 Note: Remember that in a right triangle, the hypotenuse is always the longest side.
Real-world Applications

Right triangles are not just theoretical constructs; they have practical applications in:
- Architecture, where they are used in building stability
- Navigation, for determining distances
- Surveying land to calculate heights and distances
Introduction to Trigonometry

Trigonometry is the branch of mathematics that deals with the relationships between the angles and sides of triangles. Here are the key functions:
- Sine (sin) - the ratio of the side opposite to an angle to the hypotenuse
- Cosine (cos) - the ratio of the side adjacent to an angle to the hypotenuse
- Tangent (tan) - the ratio of the side opposite to an angle to the adjacent side
| Function | Definition | Use Case |
|---|---|---|
| Sin(θ) | opposite / hypotenuse | Determining height or shadows in architecture |
| Cos(θ) | adjacent / hypotenuse | Calculating slopes in engineering or surveying |
| Tan(θ) | opposite / adjacent | Finding angles in navigation |

💡 Note: Always remember SOHCAHTOA - Sine Opposite Hypotenuse, Cosine Adjacent Hypotenuse, Tangent Opposite Adjacent.
Trigonometric Identities and Their Importance

Trigonometric identities are crucial in simplifying calculations and verifying solutions:
- Pythagorean identity: sin2θ + cos2θ = 1
- Reciprocal identities: csc(θ) = 1/sin(θ), sec(θ) = 1/cos(θ), cot(θ) = 1/tan(θ)
Unit 8: Right Triangles and Trigonometry Answers

Here’s how to approach and solve problems related to right triangles and trigonometry in Unit 8:
Solving for Side Lengths

When you are given two sides or an angle with one side:
- Use the Pythagorean Theorem to find the third side if dealing with a right triangle.
- Employ trigonometric ratios to calculate side lengths when an angle is known.
Angle Measurement

To find angles:
- Use the inverse sine, cosine, or tangent functions (arcsin, arccos, arctan) to find angles from known side ratios.
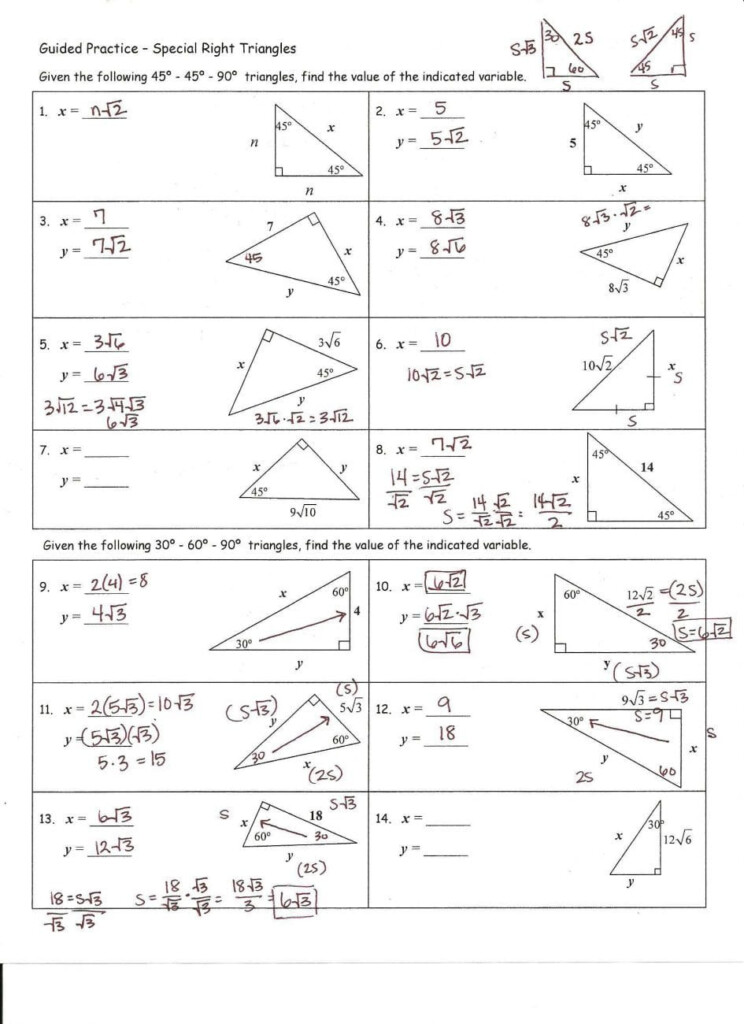
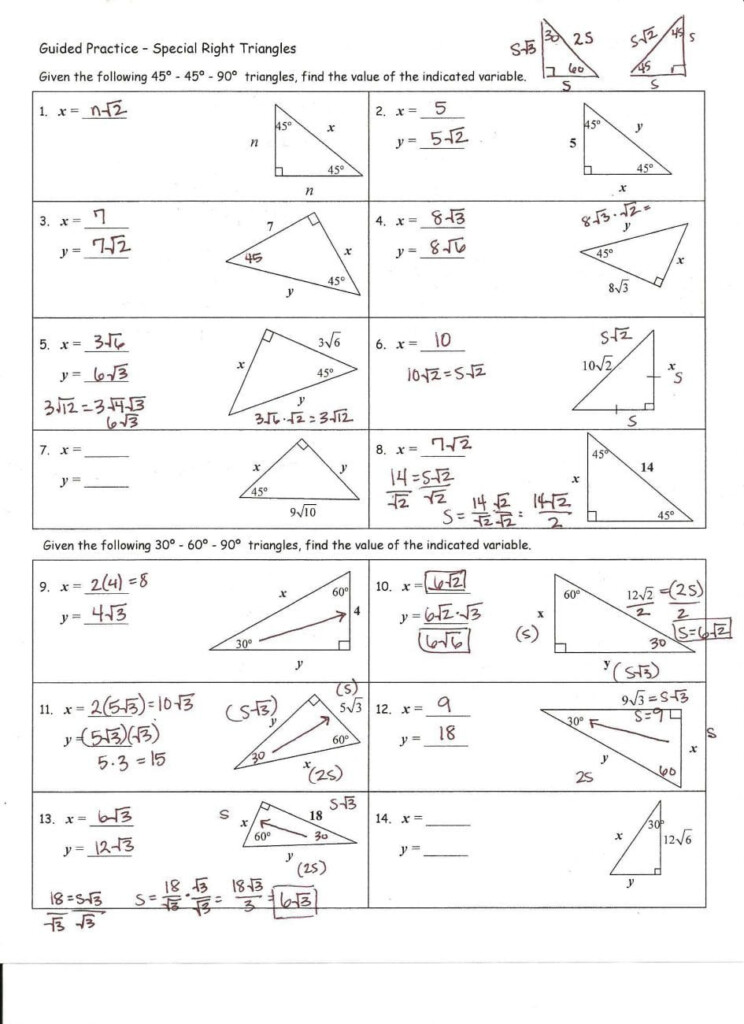
- Remember the angles of special right triangles (45-45-90 and 30-60-90 triangles).
Word Problems

Word problems often involve:
- Real-life scenarios where you need to find an unknown height or distance using trigonometric principles.
- Converting real-world measurements into geometric problems.
Example Problems

Example 1: If a right triangle has one leg of 3 cm and the hypotenuse of 5 cm, find the length of the other leg:
- Using the Pythagorean Theorem: x = √(52 - 32) = √25 - 9 = √16 = 4 cm.
Example 2: Find the angle whose tangent is 1.5:
- arctan(1.5) = θ where θ ≈ 56.31°.
Key Techniques and Hints

Here are some tips to remember while solving Unit 8 problems:
- Always draw the triangle to visualize the problem.
- Check if it’s a special triangle, which can simplify calculations.
- Use technology (like a calculator) for more complex or repetitive calculations.
🗺️ Note: If you're unsure which trigonometric function to use, look at the triangle and check which sides are known versus unknown.
Mastering Unit 8 on Right Triangles and Trigonometry is about understanding the basic principles, applying them logically, and practicing regularly. Remember, trigonometry is a tool for understanding the world around us, from the heights of mountains to the distances between stars. By following the methods outlined here, you can not only answer the questions effectively but also appreciate the beauty of geometry in our everyday life.
What are the most common types of problems in Unit 8?

+
The most common types include solving for side lengths, finding angles, and word problems related to heights and distances.
How can I remember the trigonometric ratios?
+
Use the acronym SOHCAHTOA. It stands for Sine = Opposite/Hypotenuse, Cosine = Adjacent/Hypotenuse, Tangent = Opposite/Adjacent.
Are there any tricks to quickly solve problems involving right triangles?

+
Yes, recognizing special triangles like 45-45-90 and 30-60-90 can save time. Also, understanding the relationships between angles and sides (using complementary angles, for instance) can speed up problem-solving.
What tools can help in solving trigonometry problems?

+
A scientific calculator, geometry software, or online trigonometry calculators are very useful, especially for complex or repetitive calculations.
Why is trigonometry important in real life?
+Trigonometry helps in navigation, architecture, engineering, surveying, game development, and many other fields by providing methods to calculate distances, heights, angles, and proportions.