Master Two Step Inequality Word Problems with Ease

Understanding two-step inequalities is crucial for students venturing into advanced mathematics. These inequalities, which involve solving for variables with at least two operations, pave the way for solving more complex algebraic problems. This guide provides a comprehensive walkthrough on how to master two-step inequality word problems, ensuring students can tackle these challenges with confidence.
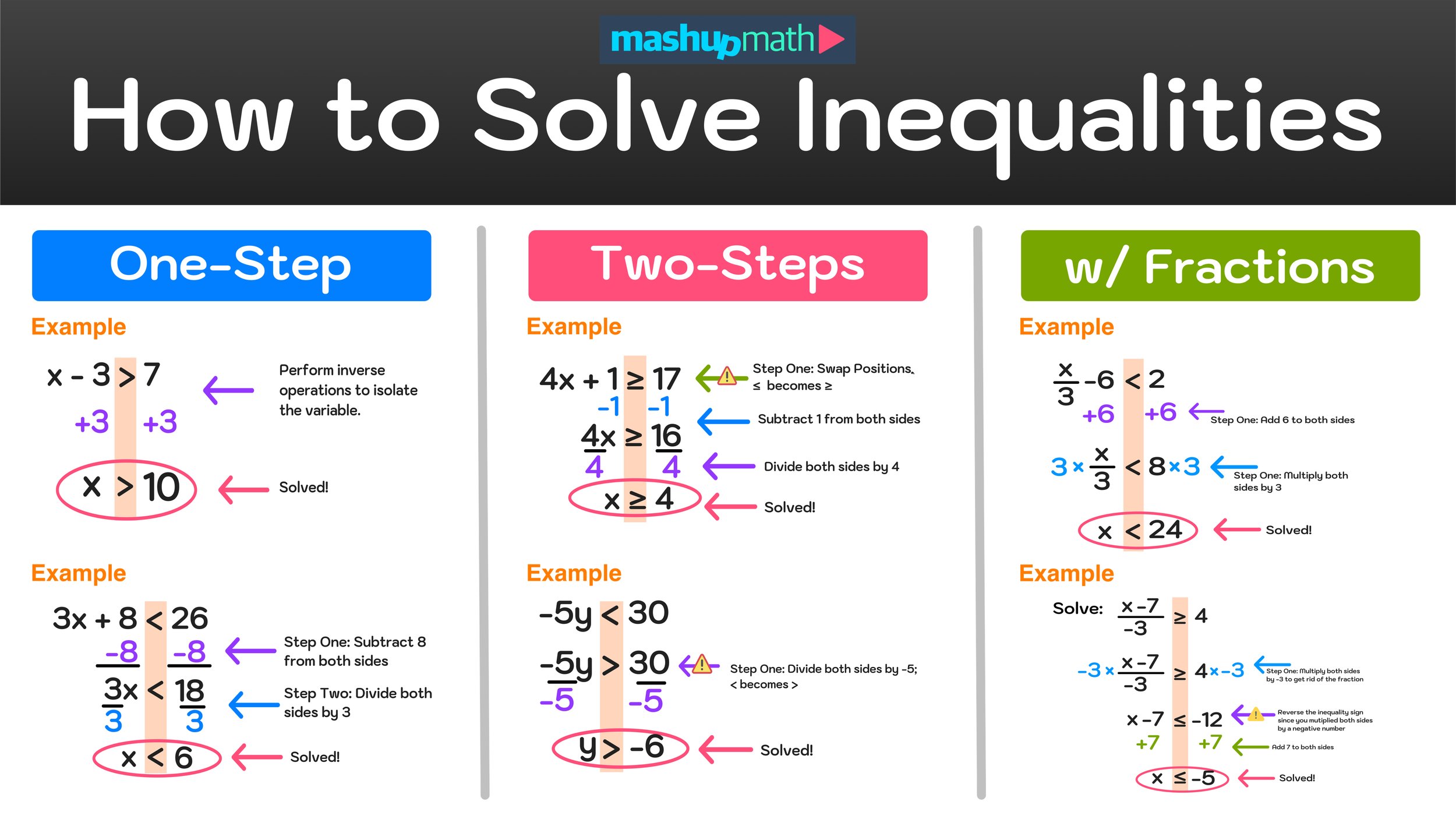
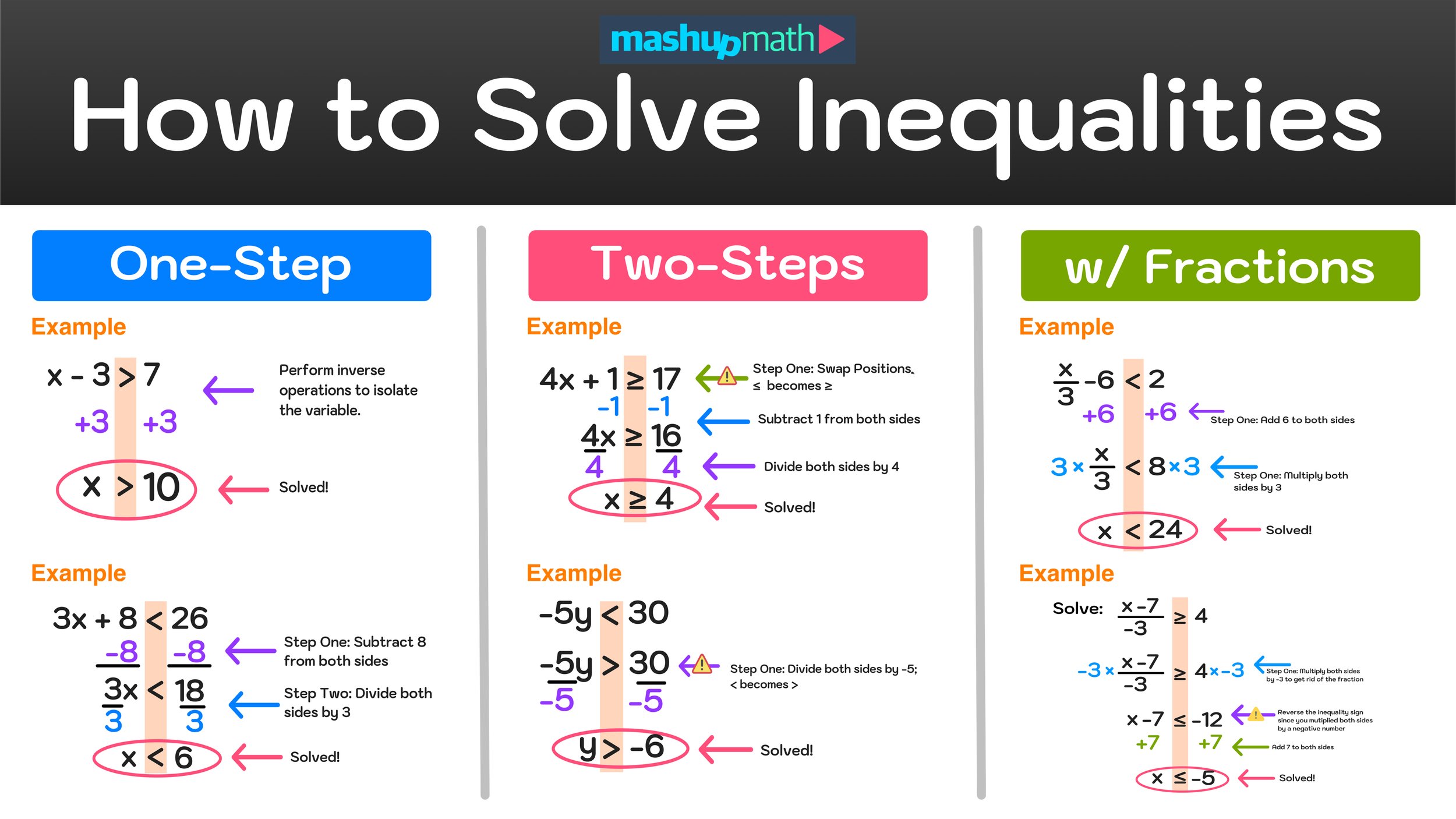
What Are Two-Step Inequalities?

Before diving into word problems, it’s essential to grasp the basics:
- Definition: Two-step inequalities involve applying two or more steps to isolate the variable on one side of the inequality sign.
- Common Operations: Addition, subtraction, multiplication, and division are commonly used to solve these inequalities.
Here’s an example to illustrate:

To solve 3x + 2 > 11:
- Subtract 2 from both sides to isolate the term with x: 3x > 9.
- Then, divide both sides by 3 to solve for x: x > 3.
Translating Word Problems into Inequalities

Translating word problems into mathematical expressions or inequalities requires a step-by-step approach:
- Identify Key Words: Look for words like 'at least', 'no more than', 'less than', and 'greater than' which indicate inequalities.
- Define Variables: Clearly define what each variable represents in the problem.
- Create the Inequality: Formulate the inequality based on the information provided.
📚 Note: The most common trap in word problems is misinterpreting the condition. Remember, 'at least' and 'no more than' are inclusive, so you should use ≤ or ≥ accordingly.
Solving Two-Step Inequality Word Problems
Let’s delve into solving some practical two-step inequality word problems:
Example 1:

Sam wants to save at least 1000 for his trip. He already has 450. How much more does he need to save per month if he wants to reach his goal in no more than 6 months?
- Define Variable: Let x be the amount Sam needs to save each month.
- Set Up the Inequality: 450 + 6x ≥ 1000.
To solve:
- Subtract 450 from both sides: 6x ≥ 550.
- Divide by 6: x ≥ 91.667.
Sam needs to save at least $91.67 per month.
Example 2:
A bus can carry no more than 45 passengers, and each passenger pays 25. How many passengers can board the bus if it has made 750 so far?
- Define Variable: Let p be the number of passengers who have paid.
- Set Up the Inequality: 25p ≤ 1125.
To solve:
- Divide by 25: p ≤ 45.
The bus can carry up to 45 passengers, so it can still board additional passengers up to this limit.
| Passengers Paid (p) | Income ($) | Remaining Capacity |
|---|---|---|
| 30 | 750 | 15 |

Common Mistakes to Avoid

When working with inequalities, certain pitfalls can lead to errors:
- Not Reversing the Inequality Sign: When multiplying or dividing both sides by a negative number, remember to reverse the inequality sign.
- Omitting Steps: Ensure all operations are applied consistently to both sides of the inequality.
- Misinterpreting the Problem: Pay close attention to what the problem is asking for, especially terms like ‘at least’ or ‘no more than’.
Advanced Techniques and Tips
For more complex problems or to accelerate your problem-solving:
- Graphing: Visualizing inequalities on a number line can help in understanding the solution set.
- Use Substitution: Sometimes substituting values can help verify or find solutions more efficiently.
- Practice with Real-World Scenarios: Applying inequalities to real-life situations can enhance understanding and retention.
💡 Note: Familiarize yourself with terms and conditions commonly used in real-life problems to improve your ability to translate them into mathematical expressions.
In mastering two-step inequalities, the key is consistency in following the correct steps and careful attention to the language and context of the problem. By breaking down complex word problems into simpler, manageable steps, students can not only solve inequalities but also strengthen their logical reasoning and problem-solving skills. This skill set is invaluable not just for academic purposes but also in everyday life where decision-making often involves evaluating options within certain constraints. Remember, practice is the cornerstone of mastery. With each problem solved, confidence grows, and soon, what seemed complex becomes second nature.
What’s the difference between solving an equation and an inequality?

+
An equation aims to find a single solution where both sides are equal. In contrast, an inequality finds a range of values that make the statement true, involving terms like greater than, less than, or their inclusive versions.
Why do we need to reverse the inequality sign when dividing by a negative number?

+
Reversing the inequality sign maintains the truth of the inequality. When you multiply or divide both sides by a negative number, you essentially flip the direction of the comparison, so the sign must flip as well.
How can I check if my solution to an inequality is correct?
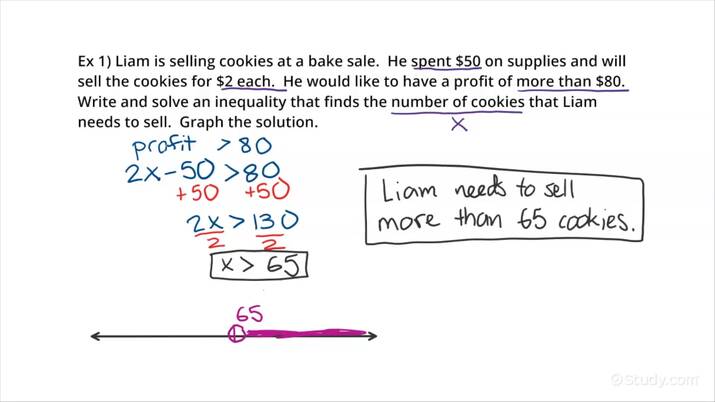
+
Select a value within your solution set and substitute it back into the original inequality. If the inequality holds true, your solution is correct.