Solve Two-Step Inequalities: Word Problems Worksheet

Word problems involving two-step inequalities present a challenging yet rewarding aspect of algebra education. These problems not only test a student's grasp of algebraic manipulation but also require an understanding of real-world scenarios where inequalities come into play. In this article, we will explore how to set up and solve two-step inequalities through word problems, giving you a structured approach to mastering this important algebraic skill.

Understanding Two-Step Inequalities

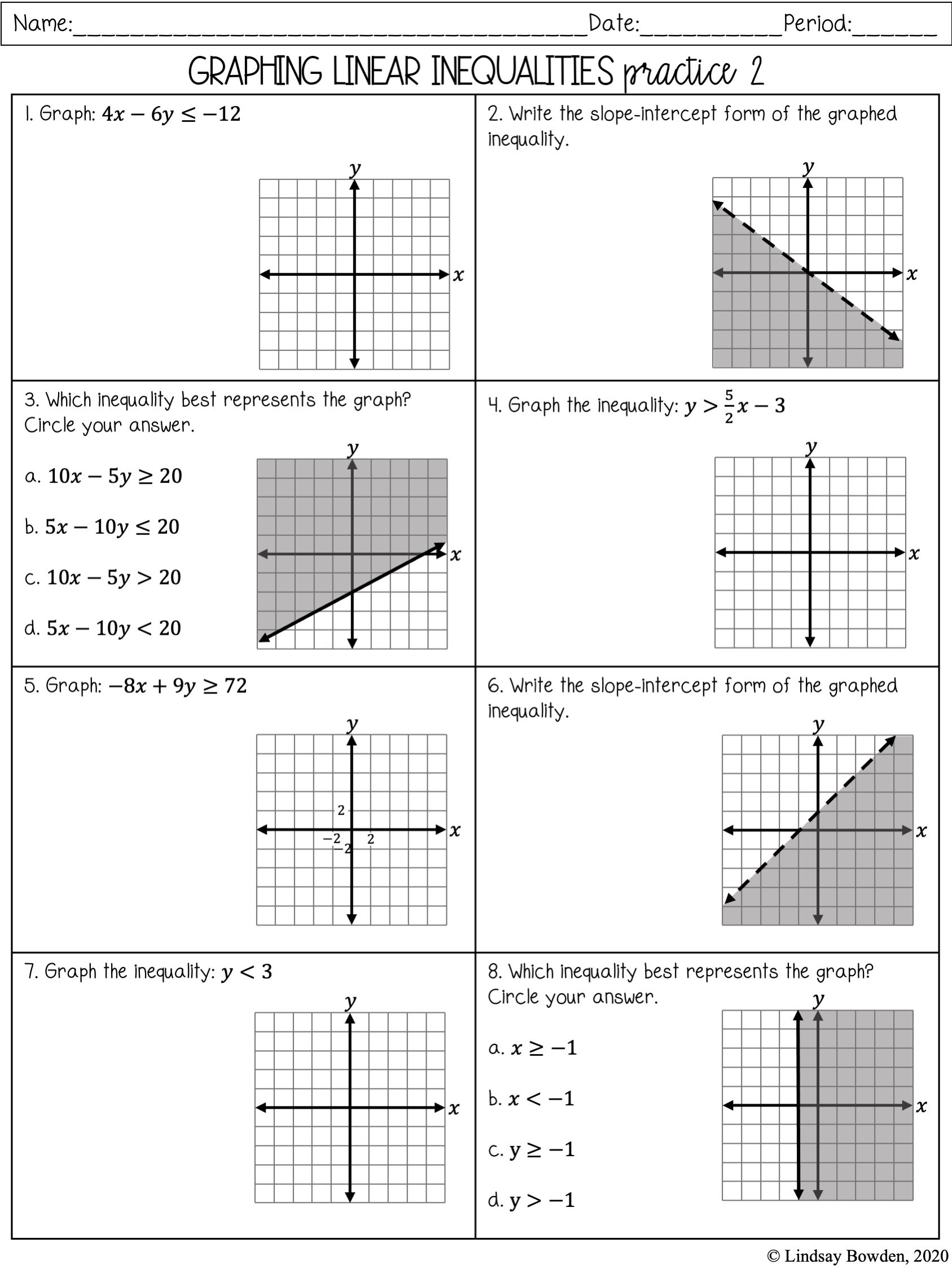
Two-step inequalities are inequalities where you need to perform two operations to solve for the variable. These operations typically involve addition, subtraction, multiplication, or division, but unlike equations, inequalities have a range of solutions rather than a single answer. Here's what they usually look like:

• 2x + 5 > 15
• 4 - 3y ≤ -8

The process of solving involves isolating the variable in much the same way as solving equations, but with an extra step for inequality notation:

1. First Step: Perform an operation that isolates the variable term.
2. Second Step: Perform an operation to isolate the variable itself.
3. Remember: When multiplying or dividing both sides of an inequality by a negative number, you must reverse the inequality sign.

Solving Two-Step Inequalities: A Step-by-Step Guide

Here's how you would approach a typical two-step inequality:

Example Problem

Anne has saved $50 for a concert ticket. If she earns $10 each week from her part-time job, how many weeks does she need to work to afford a ticket that costs at least $150?

We start by setting up the inequality:

• Let w be the number of weeks.
• The total amount Anne will have after working w weeks is 50 + 10w.
• We want this amount to be greater than or equal to $150.

50 + 10w ≥ 150

Now, let's solve this inequality:

1. Subtract 50 from both sides: 10w ≥ 100
2. Divide both sides by 10: w ≥ 10

This means Anne needs to work for at least 10 weeks to afford the ticket. Here are the steps in detail:

- Start with the inequality: 50 + 10w ≥ 150
- Subtract 50 from both sides to isolate the variable term:
    - 50 + 10w - 50 ≥ 150 - 50
    - 10w ≥ 100
- Divide both sides by 10 to isolate w:
    - 10w / 10 ≥ 100 / 10
    - w ≥ 10

📝 Note: Always reverse the inequality sign when dividing or multiplying both sides by a negative number.

Another Example

At a bakery, each muffin costs $2, and they also sell cookies at $3 each. John has $12 to spend on snacks. How many cookies can he buy if he wants to buy at least 2 muffins?

• Let m be the number of muffins, and c be the number of cookies.
• John wants at least 2 muffins, so m ≥ 2.
• The total cost must not exceed $12: 2m + 3c ≤ 12.

We need to determine the maximum number of cookies (c) John can buy while still meeting his minimum muffin requirement:

1. Substitute the minimum value for muffins: 2 * 2 + 3c ≤ 12.
2. Simplify: 4 + 3c ≤ 12.
3. Subtract 4 from both sides: 3c ≤ 8.
4. Divide by 3: c ≤ 2.67.

Since John cannot buy a fraction of a cookie, he can buy at most 2 cookies. Here are the detailed steps:

- Start with the inequality: 2 * 2 + 3c ≤ 12
- Simplify to isolate the variable term:
    - 4 + 3c ≤ 12
- Subtract 4 from both sides to isolate the variable:
    - 4 + 3c - 4 ≤ 12 - 4
    - 3c ≤ 8
- Divide both sides by 3:
    - 3c / 3 ≤ 8 / 3
    - c ≤ 2.67 (John can buy at most 2 cookies)

Practical Applications

Two-step inequalities are not just academic exercises; they have real-world applications:

• Financial Planning: Budgeting, saving, and understanding the affordability of expenses over time.
• Inventory Management: Determining how many of an item you can produce or order based on cost constraints.
• Time Management: Planning how much time to allocate to different activities or projects.

By mastering two-step inequalities, you are equipped to handle scenarios where decisions depend on constraints like time, money, or resources.

Summary

In this post, we delved into the world of solving two-step inequalities through word problems. We explored how to set up inequalities based on real-life situations, demonstrated the steps required to solve them, and highlighted their practical applications. Remember, each inequality you solve builds your problem-solving skills, which are invaluable in both academic and real-world settings. Always check your work for accuracy, and keep practicing with different types of problems to reinforce your understanding.

What’s the difference between a two-step equation and a two-step inequality?

+

A two-step equation has one specific solution, while a two-step inequality has a range of solutions, often written using the symbols <, ≤, >, or ≥.

Why do we reverse the inequality sign when multiplying or dividing by a negative number?

+

The sign must be reversed to maintain the relationship between the values because multiplication or division by a negative number reverses the order of the numbers on the number line.

Can I use inequalities to model situations in finance or economics?

+

Yes, inequalities can model constraints like budget limits, loan repayments, and investment thresholds.