7 Ways to Solve Two-Step Equations

Solving two-step equations is a fundamental skill in mathematics, particularly in algebra. These equations require two operations to solve, and understanding how to tackle them can greatly enhance your problem-solving abilities. Here’s a comprehensive guide on how to solve two-step equations using various methods and techniques.
Understanding Two-Step Equations

A two-step equation is a type of linear equation that requires two steps to solve. These equations are typically in the form of ax ± b = c, where a, b, and c are constants, and x is the variable we’re trying to solve for.
Method 1: Using Addition and Subtraction

When dealing with two-step equations involving addition and subtraction, our primary goal is to isolate the variable on one side of the equation. Let’s consider an example:
2x + 5 = 11
Step 1: Subtract 5 from both sides of the equation to eliminate the constant term.
2x + 5 - 5 = 11 - 5 2x = 6
Step 2: Divide both sides of the equation by 2 to solve for x.
2x / 2 = 6 / 2 x = 3
Method 2: Using Multiplication and Division

Two-step equations involving multiplication and division require a different approach. Our objective is still to isolate the variable, but we’ll use multiplication and division operations to achieve this. Let’s look at an example:
4x / 2 = 6
Step 1: Multiply both sides of the equation by 2 to eliminate the fraction.
(4x / 2) × 2 = 6 × 2 4x = 12
Step 2: Divide both sides of the equation by 4 to solve for x.
4x / 4 = 12 / 4 x = 3
Method 3: Using a Combination of Operations

Sometimes, two-step equations involve a combination of addition, subtraction, multiplication, and division operations. In these cases, we need to apply the operations in the correct order to solve for the variable. Let’s consider an example:
2x + 3 = 9
Step 1: Subtract 3 from both sides of the equation to eliminate the constant term.
2x + 3 - 3 = 9 - 3 2x = 6
Step 2: Divide both sides of the equation by 2 to solve for x.
2x / 2 = 6 / 2 x = 3
Method 4: Using the Inverse Operation

Another approach to solving two-step equations is to use the inverse operation. This involves applying the opposite operation to both sides of the equation to isolate the variable. Let’s look at an example:
x / 3 + 2 = 5
Step 1: Subtract 2 from both sides of the equation to eliminate the constant term.
x / 3 + 2 - 2 = 5 - 2 x / 3 = 3
Step 2: Multiply both sides of the equation by 3 to solve for x.
(x / 3) × 3 = 3 × 3 x = 9
Method 5: Using Balancing Equations
Balancing equations is a useful technique for solving two-step equations. This involves applying the same operation to both sides of the equation to maintain the balance. Let’s consider an example:
x - 2 = 7
Step 1: Add 2 to both sides of the equation to eliminate the constant term.
x - 2 + 2 = 7 + 2 x = 9
Method 6: Using Algebraic Properties

Algebraic properties, such as the distributive property and the commutative property, can be useful in solving two-step equations. Let’s look at an example:
2(x + 3) = 12
Step 1: Distribute the 2 to the terms inside the parentheses.
2x + 6 = 12
Step 2: Subtract 6 from both sides of the equation to eliminate the constant term.
2x + 6 - 6 = 12 - 6 2x = 6
Step 3: Divide both sides of the equation by 2 to solve for x.
2x / 2 = 6 / 2 x = 3
Method 7: Using Real-World Applications

Two-step equations have numerous real-world applications, such as calculating the cost of goods, determining the area of a room, and measuring the speed of a vehicle. Let’s consider an example:
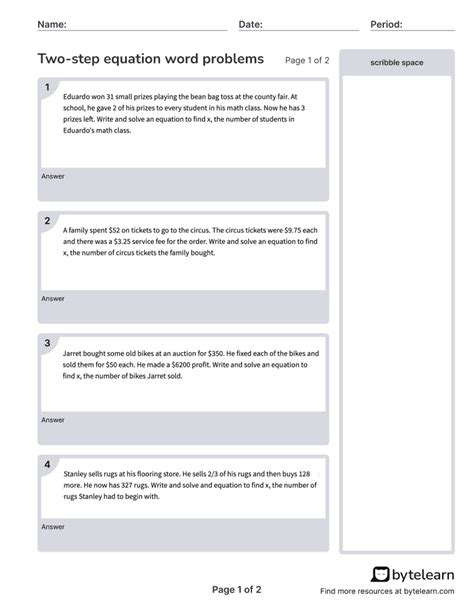
Tom has 120 to spend on clothes. He buys a shirt for 20 and wants to buy a pair of pants that costs x. If he has 60 left after buying the shirt, how much can he spend on the pants?
Step 1: Set up the equation based on the problem.
20 + x = 60
Step 2: Subtract 20 from both sides of the equation to eliminate the constant term.
20 + x - 20 = 60 - 20 x = 40
Conclusion

Solving two-step equations requires a combination of mathematical operations, algebraic properties, and real-world applications. By mastering these techniques, you’ll be able to tackle a wide range of problems and develop a deeper understanding of mathematical concepts. Remember to always read the problem carefully, identify the variables and constants, and apply the correct operations to solve for the unknown value.
FAQ Section

What is a two-step equation?
+A two-step equation is a type of linear equation that requires two operations to solve.
How do I solve a two-step equation?
+To solve a two-step equation, you need to apply two operations, such as addition and subtraction, or multiplication and division, to isolate the variable.
What are some common techniques for solving two-step equations?
+Some common techniques for solving two-step equations include using addition and subtraction, multiplication and division, inverse operations, balancing equations, algebraic properties, and real-world applications.