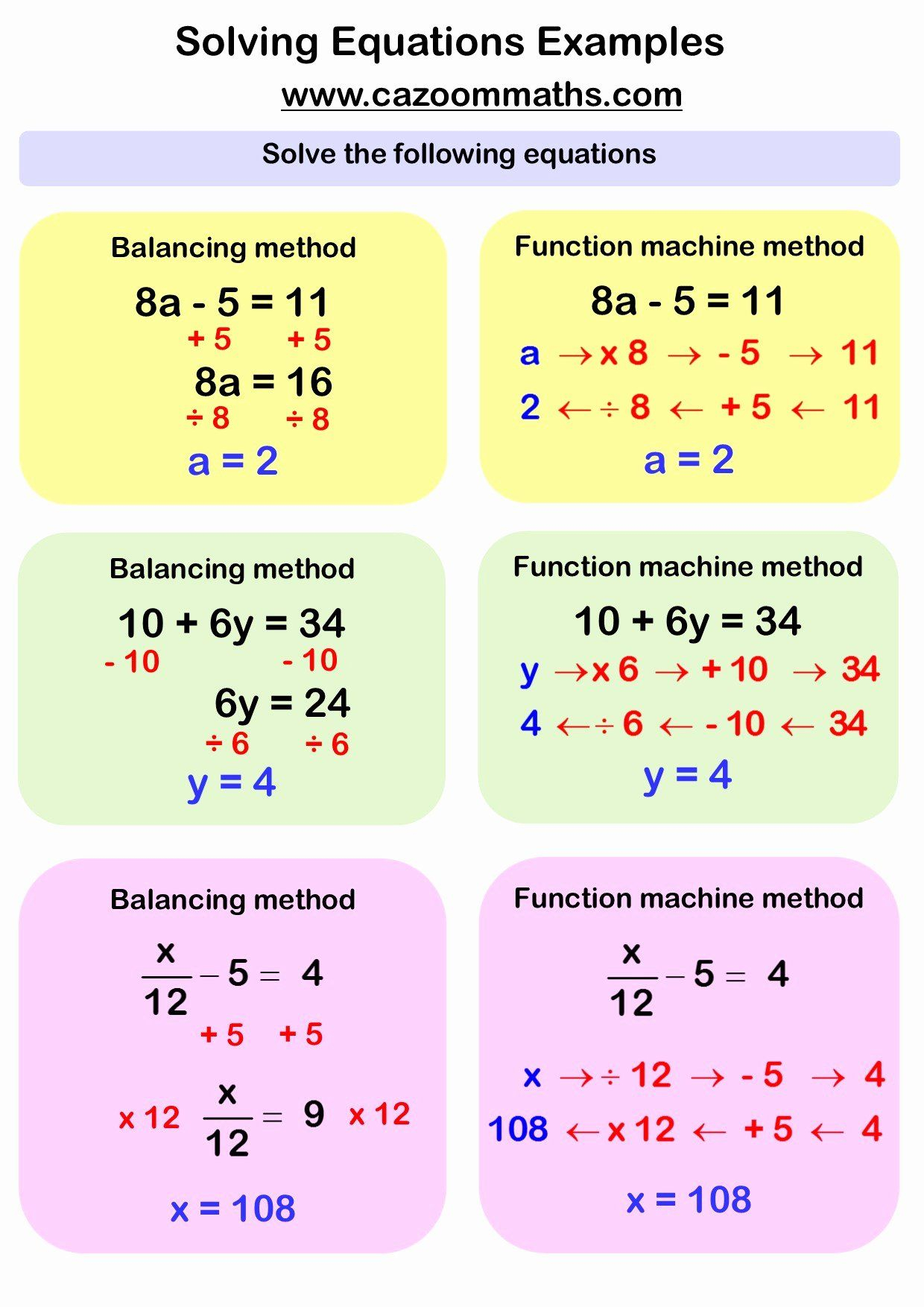
Solve Two-Step Equations with Fractional Coefficients Easily

Solving Two-Step Equations with Fractional Coefficients

Mathematics can often seem daunting when you're faced with equations involving fractions. However, once you understand the steps to solve two-step equations with fractional coefficients, you'll find that they're quite manageable and follow a logical pattern.
The Basics of Two-Step Equations

Before diving into the intricacies of fractional coefficients, let's recall the basic structure of a two-step equation:
- The first step typically involves removing an addition or subtraction term from one side of the equation.
- Then, the second step deals with isolating the variable by eliminating the coefficient through division or multiplication.
Handling Fractions in Equations

Fractions can appear in two main ways in two-step equations:
- As coefficients next to the variable.
- As constant terms on either side of the equation.
Here are the steps to handle these:
- Isolate the term with the variable: Add or subtract to move all other terms to one side.
- Convert fractions to whole numbers: Multiply both sides by the least common multiple (LCM) of the denominators if necessary to simplify.
- Solve for the variable: Divide or multiply to get the variable by itself.
Step-by-Step Guide

Let's walk through an example to demonstrate how to apply these steps:
Consider the equation:
2/3x + 1 = 7
Step 1: Isolate the term with the variable
Subtract 1 from both sides:
2/3x = 6
Step 2: Eliminate the fractional coefficient
Here, you'll want to get rid of the fraction. Multiply both sides by the reciprocal of the coefficient (which is 3/2 in this case):
(3/2) * (2/3x) = (3/2) * 6
This simplifies to:
x = 9
Managing More Complex Fractions

In some cases, you might encounter more complex fractions or improper fractions:
| Example | Solution Steps |
|---|---|
| 7/8x - 3/2 = 4 |
|
It's essential to ensure that all fractions are converted into a format where you can perform standard arithmetic operations without confusion.
🌟 Note: When converting improper fractions, you might want to use mixed numbers or decimal forms to make further calculations easier. However, for exact answers in algebra, it's often preferable to keep the fraction in its original form unless otherwise directed.
Troubleshooting Common Mistakes

Here are some common errors to avoid:
- Mistake in sign changes: Always remember that any operation done to one side of the equation must be mirrored on the other side, with particular attention to the sign.
- Incorrect multiplication or division: When removing the fraction, ensure you multiply or divide by the reciprocal.
- Skipping steps: Follow the methodical steps laid out above without shortcutting or skipping key operations.
The key to mastering these equations is practice and understanding the logic behind each step.
In sum, solving two-step equations with fractional coefficients requires you to: isolate the variable term, eliminate the fraction by appropriate multiplication or division, and finally solve for the variable. By keeping these steps in mind and practicing regularly, you’ll become adept at handling these equations, turning what might seem like complex math into routine tasks.
✨ Note: It's always good to check your work by substituting the solution back into the original equation to ensure it balances out correctly.
What if I encounter a negative fractional coefficient?

+
Handle negative fractions similarly to positive ones, but remember to keep track of the signs. When dividing or multiplying by a negative number, the inequality sign will flip.
Can I simplify the equation by reducing the fractions first?

+
Yes, you can simplify fractions if possible, but it’s often easier to proceed by eliminating the coefficients as is to avoid potential confusion or errors in simplification.
What if both sides of the equation have fractions?

+
If both sides have fractions, you can clear them by multiplying the entire equation by the LCM of all the denominators involved. This simplifies the equation into whole numbers, making the solving process easier.