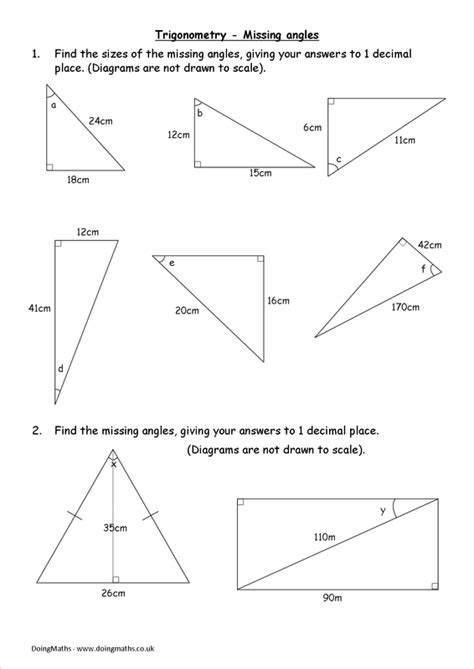
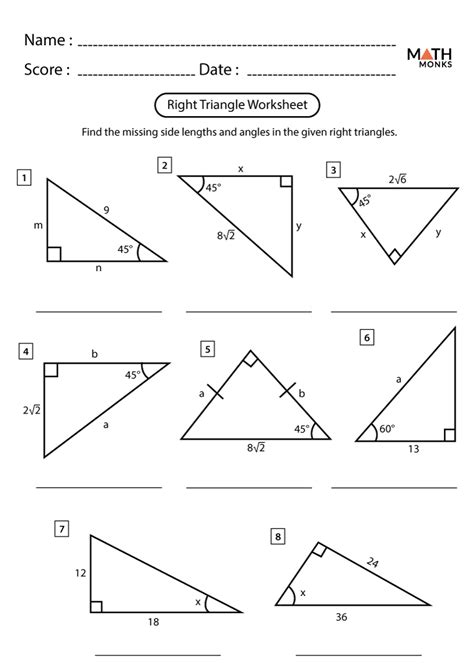
Trigonometry Worksheet Answers: Find Missing Sides Easily
Trigonometry Basics: A Refresher
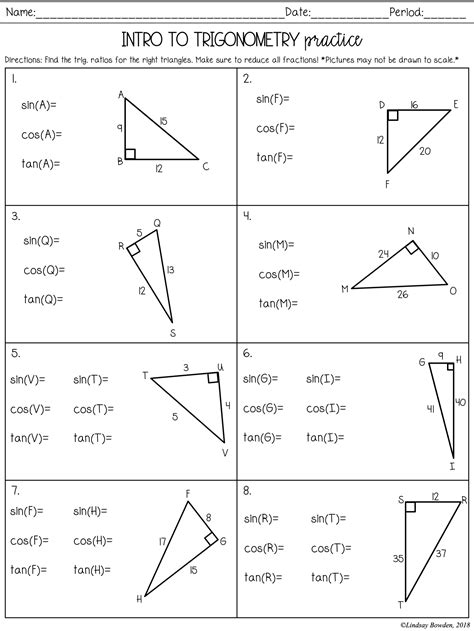
Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. It involves the use of trigonometric functions such as sine, cosine, and tangent to solve problems. In this blog post, we will focus on finding missing sides of triangles using trigonometry.
Understanding Trigonometric Functions
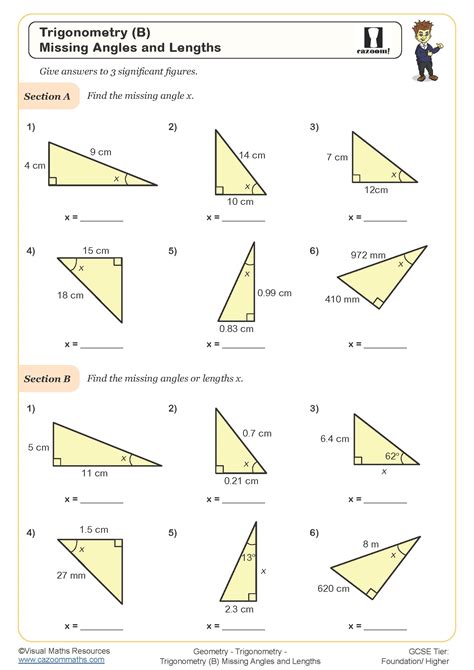
Trigonometric functions are used to relate the angles of a triangle to the ratios of the lengths of its sides. The three basic trigonometric functions are:
- Sine (sin): The ratio of the length of the side opposite the angle to the length of the hypotenuse.
- Cosine (cos): The ratio of the length of the side adjacent to the angle to the length of the hypotenuse.
- Tangent (tan): The ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
Using Trigonometry to Find Missing Sides
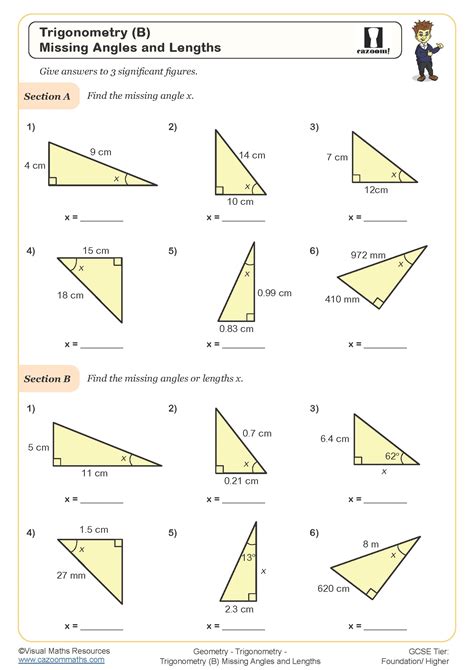
To find missing sides of a triangle using trigonometry, we need to know the length of at least one side and the measure of one angle. We can then use the trigonometric functions to set up equations and solve for the unknown sides.
Method 1: Using the Sine Function
If we know the length of the hypotenuse and the measure of one angle, we can use the sine function to find the length of the side opposite the angle.
sin(A) = opposite side / hypotenuse
For example, if we know the length of the hypotenuse is 10 cm and the measure of angle A is 30°, we can find the length of the side opposite angle A using the sine function:
sin(30°) = opposite side / 10
Method 2: Using the Cosine Function
If we know the length of the hypotenuse and the measure of one angle, we can use the cosine function to find the length of the side adjacent to the angle.
cos(A) = adjacent side / hypotenuse
For example, if we know the length of the hypotenuse is 10 cm and the measure of angle A is 60°, we can find the length of the side adjacent to angle A using the cosine function:
cos(60°) = adjacent side / 10
Method 3: Using the Tangent Function
If we know the length of the side opposite the angle and the measure of one angle, we can use the tangent function to find the length of the side adjacent to the angle.
tan(A) = opposite side / adjacent side
For example, if we know the length of the side opposite angle A is 6 cm and the measure of angle A is 45°, we can find the length of the side adjacent to angle A using the tangent function:
tan(45°) = 6 / adjacent side
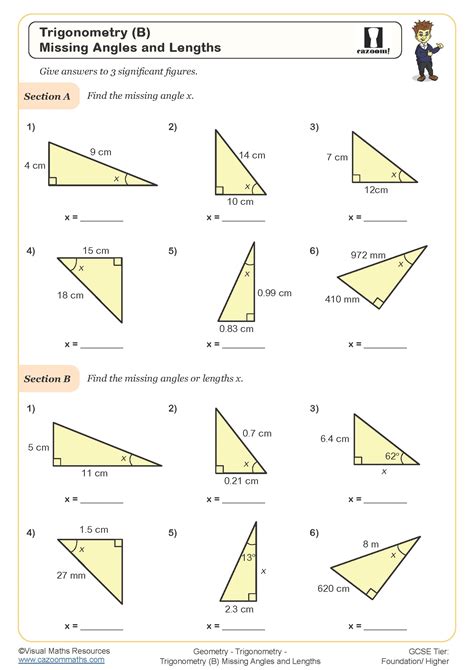
Trigonometry Worksheet Answers
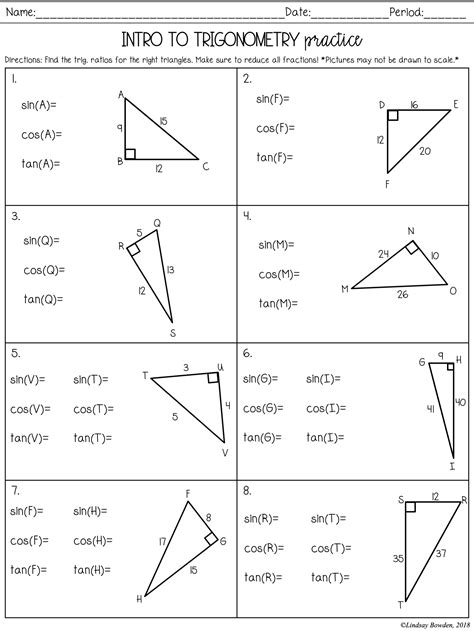
Here are some examples of trigonometry problems with answers:
| Problem | Answer |
|---|---|
| In a right triangle, the length of the hypotenuse is 15 cm and the measure of angle A is 40°. Find the length of the side opposite angle A. | sin(40°) = opposite side / 15 opposite side = 15 x sin(40°) = 9.66 cm |
| In a right triangle, the length of the hypotenuse is 20 cm and the measure of angle A is 60°. Find the length of the side adjacent to angle A. | cos(60°) = adjacent side / 20 adjacent side = 20 x cos(60°) = 10 cm |
| In a right triangle, the length of the side opposite angle A is 8 cm and the measure of angle A is 30°. Find the length of the side adjacent to angle A. | tan(30°) = 8 / adjacent side adjacent side = 8 / tan(30°) = 13.86 cm |
📝 Note: The answers are rounded to two decimal places for simplicity.
Conclusion
Finding missing sides of triangles using trigonometry is a straightforward process that involves using the trigonometric functions to set up equations and solve for the unknown sides. By understanding the sine, cosine, and tangent functions, we can easily find missing sides of triangles. Remember to always check your work and use a calculator to ensure accuracy.
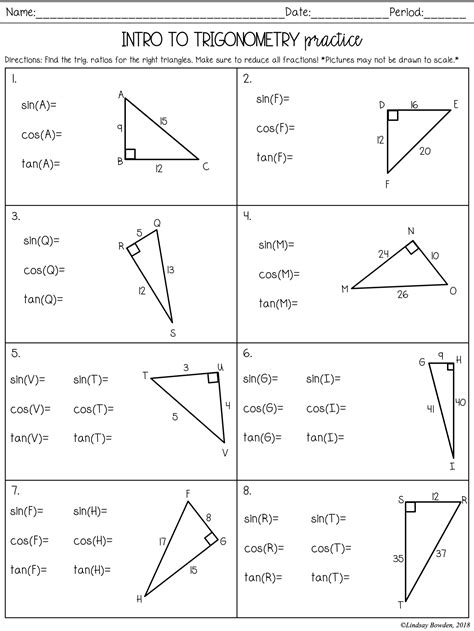
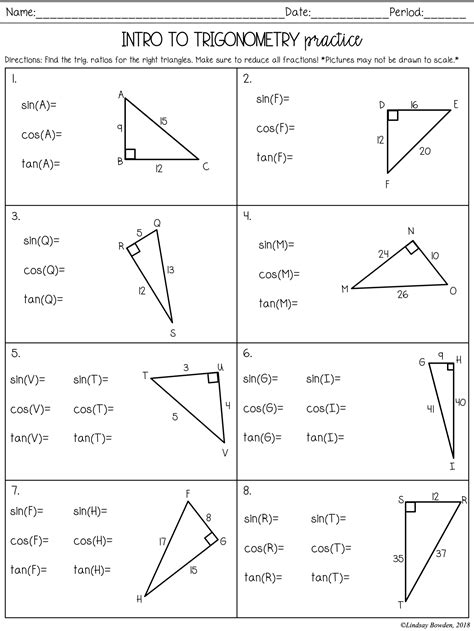
What is the difference between sine, cosine, and tangent?
+
The sine, cosine, and tangent functions are used to relate the angles of a triangle to the ratios of the lengths of its sides. The sine function relates the length of the side opposite the angle to the length of the hypotenuse, the cosine function relates the length of the side adjacent to the angle to the length of the hypotenuse, and the tangent function relates the length of the side opposite the angle to the length of the side adjacent to the angle.
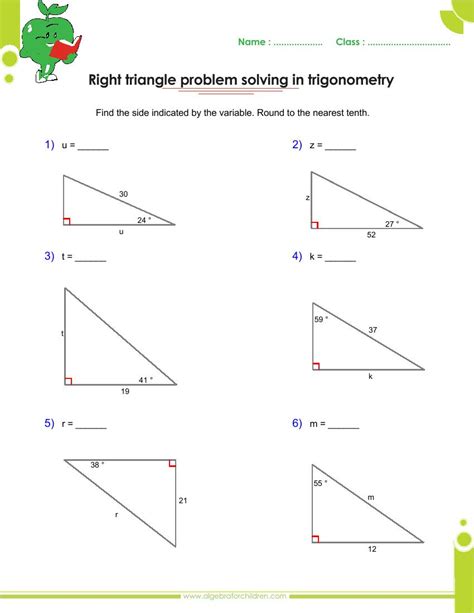
How do I use trigonometry to find missing sides of triangles?
+
To find missing sides of triangles using trigonometry, you need to know the length of at least one side and the measure of one angle. You can then use the trigonometric functions to set up equations and solve for the unknown sides.
What is the importance of trigonometry in real-life applications?
+
Trigonometry has numerous real-life applications in fields such as physics, engineering, navigation, and computer science. It is used to calculate distances, heights, and angles in various contexts, including building design, surveying, and astronomy.
Related Terms:
- Trigonometry Worksheet with answers PDF
- Trigonometry Finding missing sides Worksheet
- trigonometry finding side lengths worksheet
- trig worksheets with answer key
- solving right triangles trigonometry worksheet
- trigonometry solve for angle worksheet