Trig Ratios Worksheet: Boost Your Math Skills Quickly

Are you finding the world of trigonometry a bit challenging? Whether you're a student in high school math or just looking to refresh your skills, understanding trigonometric ratios can unlock a plethora of mathematical capabilities. Let's dive deep into trig ratios to not only boost your math skills but make learning enjoyable and effective.
What are Trigonometric Ratios?

Trigonometry deals with the relationships between the sides and angles of triangles, particularly right-angled triangles. Here are the primary trigonometric ratios:
- Sine (sin) - The ratio of the length of the opposite side to the hypotenuse.
- Cosine (cos) - The ratio of the length of the adjacent side to the hypotenuse.
- Tangent (tan) - The ratio of the length of the opposite side to the adjacent side.
📝 Note: These ratios are crucial for calculating angles and sides in any right-angled triangle.
Why Are Trig Ratios Important?

Trigonometry isn’t just about triangles; it’s integral in:
- Navigation - determining distances or bearings.
- Physics - analyzing wave patterns and forces.
- Engineering - designing structures and calculating angles.
How to Use Trig Ratios?
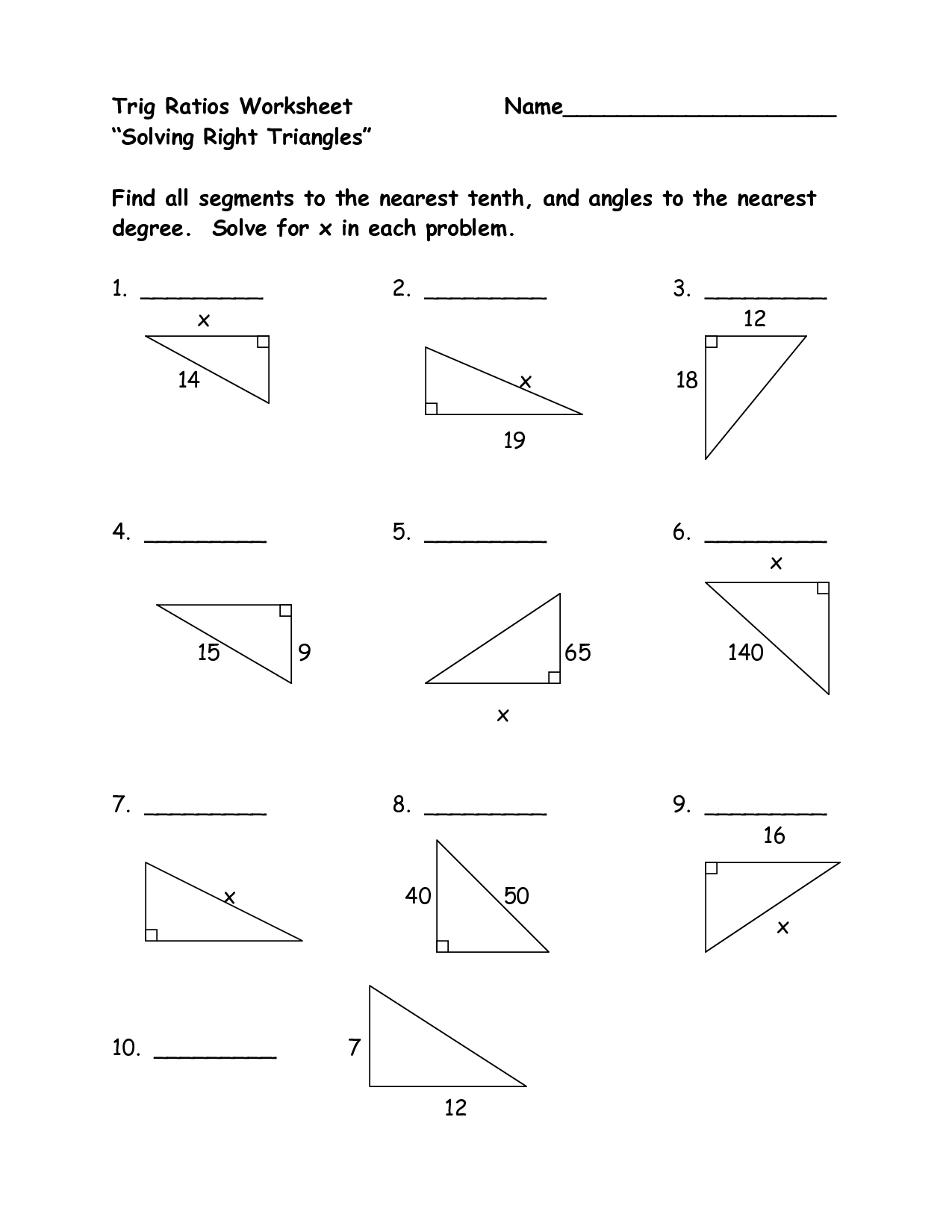
Here’s a step-by-step guide to effectively utilize trigonometric ratios:
- Identify the right triangle: Ensure you’re working with a right-angled triangle.
- Label the sides:
- Opposite: The side opposite the angle you’re focusing on.
- Adjacent: The side adjacent or next to the angle.
- Hypotenuse: The longest side opposite the right angle.
- Choose the correct ratio: Based on what you need to find:
Ratio To Find When to Use Sin Angle or Opposite side Angle and hypotenuse known Cos Angle or Adjacent side Angle and hypotenuse known Tan Angle or Opposite to Adjacent Angle and one of the other sides known 
- Set up the equation: Use the ratio to form an equation. For example, if you’re finding the sine of an angle:
📝 Note: Trigonometric ratios are directly proportional to the angles of the triangle.
Worksheet Example

Let’s apply this knowledge with an example:
- Given the angle ( \theta ) is 30 degrees, and the adjacent side is 5 units, calculate the hypotenuse.
- We use cosine: [ \cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}} ] [ \cos(30) = \frac{5}{h} \Rightarrow \frac{\sqrt{3}}{2} = \frac{5}{h} \Rightarrow h = \frac{10}{\sqrt{3}} \approx 5.77 \text{ units} ]
Advanced Trigonometry

As you progress, you’ll encounter more ratios like:
- Cosecant (csc) - Reciprocal of sine: ( \csc(\theta) = \frac{1}{\sin(\theta)} )
- Secant (sec) - Reciprocal of cosine: ( \sec(\theta) = \frac{1}{\cos(\theta)} )
- Cotangent (cot) - Reciprocal of tangent: ( \cot(\theta) = \frac{1}{\tan(\theta)} )
Understanding these will allow you to approach complex trigonometric problems with confidence.
By familiarizing yourself with these concepts, you can not only solve trigonometry problems but also better understand related mathematical disciplines.
Why do I need to learn trigonometry?

+
Trigonometry is essential in various fields like physics, architecture, engineering, and computer graphics, where it helps in calculating distances, angles, and wave forms.
What’s the difference between sin, cos, and tan?

+
Sine relates to the ratio of the opposite side to the hypotenuse. Cosine is the adjacent side to the hypotenuse ratio. Tangent is the ratio of the opposite to the adjacent side.
Can trig ratios be used in real life?

+
Yes, they are used in navigation to calculate distances, in construction to ensure stability, in electrical engineering for AC analysis, and in many other practical applications.