Mastering Trig Proofs: Essential Worksheet Guide

The journey into trigonometric proofs can be both exhilarating and challenging. Understanding the intricacies of trigonometry is crucial for many fields, from physics and engineering to astronomy and even in computer graphics where understanding the sine and cosine of angles helps in the manipulation of digital images. This comprehensive guide is designed to simplify your journey towards mastering trigonometric proofs through a systematic worksheet approach.
Understanding the Basics of Trigonometry

Before diving into proofs, a robust foundation in basic trigonometric principles is essential.
- Right Angle Trigonometry: The SOHCAHTOA mnemonic helps remember how to compute sine, cosine, and tangent.
- Trigonometric Identities: Fundamental identities include the Pythagorean identity, sum and difference formulas, and double-angle and half-angle formulas.
Key Trigonometric Identities

| Identity | Description |
|---|---|
| sin2(x) + cos2(x) = 1 | Pythagorean Identity |
| sin(a ± b) = sin(a)cos(b) ± cos(a)sin(b) | Sum and Difference Identity |
| sin(2x) = 2sin(x)cos(x) | Double Angle Identity |
| cos(2x) = cos2(x) - sin2(x) | Double Angle Identity |
Developing a Strategy for Trigonometric Proofs

To excel in trigonometric proofs, a structured approach is necessary. Here’s a step-by-step guide:
- Identify the Goal: What must you prove? Start with the given information and work towards the statement to be proven.
- Understand Your Tools: Familiarize yourself with all trigonometric identities. Know when to apply each one.
- Manipulate the Equation: Use identities to manipulate one side of the equation to match the other.
- Check Your Work: Ensure each step logically follows the previous, and the final result matches the goal.
- Practice: Continuous practice is key. Solve various types of proofs to strengthen your understanding.
Example Proof:
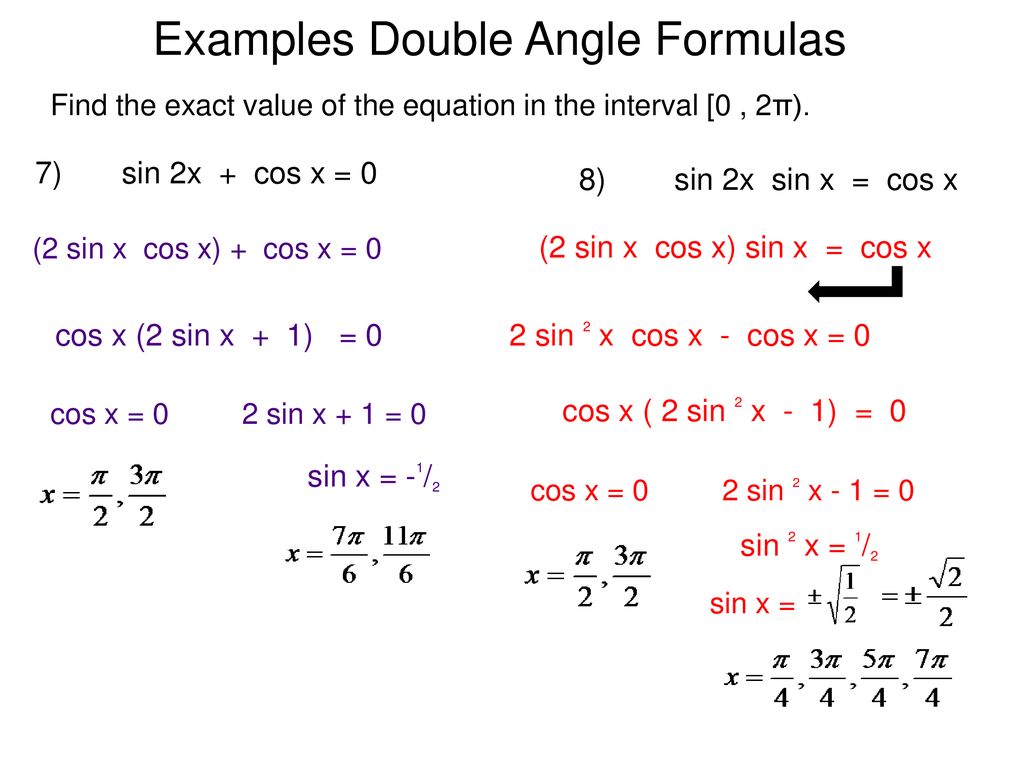
Prove the identity: sin(2x) = 2sin(x)cos(x).
Starting from the left side, use the double angle identity:
- Left Side: sin(2x)
- Apply Identity: sin(2x) = sin(2 * x)
- Double Angle Formula: sin(2 * x) = 2sin(x)cos(x)
- Thus, sin(2x) = 2sin(x)cos(x)
🚨 Note: Always ensure that each step in your proof logically follows from the previous. If you get stuck, try working backwards from the desired outcome.
Mastering Trigonometric Proofs through Worksheets

Worksheets are invaluable tools in mastering trigonometry. Here’s how they can be effectively used:
- Structured Learning: Worksheets provide a structured approach, helping you to progress logically through problems.
- Immediate Feedback: With solutions provided, you can check your work to understand your mistakes.
- Variety of Problems: They offer different problem types, ensuring comprehensive preparation.
- Building Intuition: Repeated practice helps in building an intuitive understanding of trigonometry.
Steps to Use Trigonometric Proof Worksheets:
- Choose a Suitable Worksheet: Pick one that aligns with your current knowledge level and learning goals.
- Solve Each Problem: Take your time, ensuring you understand every step.
- Review Solutions: Even if you solve the problem correctly, review the solutions to see if there are alternative methods.
- Reflect on Mistakes: If errors occur, understand where they stem from and revise relevant theory.
- Repeat and Expand: Continue practicing with worksheets that introduce new complexities.
📖 Note: Consider creating your own proof problems to test your mastery over trigonometric identities.
Advanced Trigonometric Proofs

As you progress, you’ll encounter more complex trigonometric proofs requiring a deeper understanding of trigonometric identities, algebraic manipulation, and sometimes calculus.
- Inverse Trigonometric Functions: Proofs involving arcsine, arccosine, and arctangent require familiarity with their derivatives and properties.
- Proofs Involving Limits: Some identities involve limits as they approach specific values or as functions tend to infinity.
- Integration of Trigonometric Functions: Understanding integrals of trigonometric functions can simplify complex proofs.
Pitfalls to Avoid

- Overcomplicating: Sometimes, simpler identities can be used when a more complex one seems more appropriate.
- Forgetting Negative Angles: Don’t neglect identities for negative angles which often play a crucial role in proofs.
- Ignoring Complex Numbers: Trigonometric identities extend to the complex plane, providing more versatile proofs.
⚠️ Note: Always verify your results by substituting specific values or checking trigonometric graphs to ensure accuracy.
Trigonometry is both an art and a science. Mastering trigonometric proofs through a dedicated and methodical worksheet approach will not only prepare you for academic challenges but also equip you with problem-solving skills applicable in numerous real-world scenarios. Embrace each proof as a puzzle to solve, and remember that persistence and practice will lead to profound understanding and mastery of trigonometry.
What are the most common mistakes in trigonometric proofs?

+
The most common mistakes include ignoring negative angles, not recognizing when to use simple or complex identities, and algebraic errors in manipulation. Attention to detail and thorough understanding of identities can help avoid these pitfalls.
How can I practice trigonometric proofs effectively?

+
Practice regularly, use worksheets tailored to your skill level, review mistakes, and explore alternative methods. Also, proving identities by working backward or by visualizing them on the unit circle can be very effective.
Are there any real-life applications of trigonometric proofs?

+
Absolutely! Trigonometry is crucial in fields like engineering for wave analysis, architecture for designing structures, in physics for solving problems related to motion, and in computer graphics for rendering 3D objects on a 2D plane.