5 Trig Problems Solved: Boost Your Math Skills

Solving trigonometric problems can seem daunting at first, but with practice and the right approach, you can enhance your skills significantly. Trigonometry is not just about solving triangles; it's a powerful tool used in various fields from engineering to physics, and even in modern technology like GPS. Here, we'll dive into five challenging trig problems that will not only test your skills but also offer insights into solving similar problems in the future.
Solving Trigonometric Identities
Understanding trigonometric identities is fundamental for mastering trigonometry. These identities help simplify complex expressions and solve equations with trigonometric functions more efficiently.
- Problem: Simplify the expression sin(x)cos(x) / (sin(x) + cos(x))
- Solution:
- Multiply numerator and denominator by the conjugate of the denominator (sin(x) - cos(x)):
(sin(x)cos(x)(sin(x) - cos(x))) / ((sin(x) + cos(x))(sin(x) - cos(x)))
- Which simplifies to:
(sin(x)cos(x) - sin(x)cos(x)) / (sin^2(x) - cos^2(x))
- This equals:
0 / (sin^2(x) - cos^2(x))
- Thus, the final simplified form is:
0
- Multiply numerator and denominator by the conjugate of the denominator (sin(x) - cos(x)):
💡 Note: Remember, multiplying by the conjugate can help cancel out terms in identities.
Proving Trigonometric Equations

Proving trigonometric equations can be intricate, but it’s a great way to solidify your understanding of the relationships between trigonometric functions.
- Problem: Prove that sin(4A) = 4sin(A)cos(A)cos(2A)
- Solution:
- Start with the left-hand side (LHS):
sin(4A)
- Use the angle addition formula:
sin(4A) = sin(2(2A)) = 2sin(2A)cos(2A)
- Now apply the double-angle formula for sin(2A):
2(2sin(A)cos(A))cos(2A) = 4sin(A)cos(A)cos(2A)
- Which matches the right-hand side (RHS):
4sin(A)cos(A)cos(2A)
- Start with the left-hand side (LHS):
Using Trigonometry in Real-World Applications

Trigonometry isn’t just an academic exercise. Its applications extend into numerous practical scenarios, from calculating heights of buildings to analyzing wave patterns.
- Problem: A surveyor needs to measure the height of a building. She stands 50 meters from the building and finds that the angle of elevation to the top is 45 degrees.
- Solution:
- Using the tangent function:
tan(45°) = height / 50
- Since tan(45°) equals 1:
height = 50 meters
- Using the tangent function:
Solving Complex Trigonometric Equations
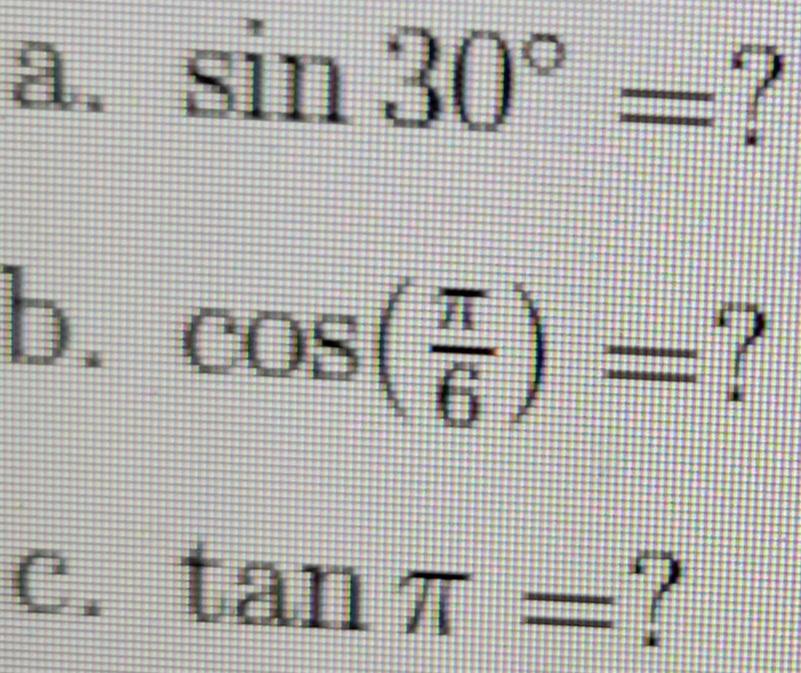
Solving equations involving multiple trigonometric functions can test your knowledge of trigonometric principles deeply.
- Problem: Solve for sin(x)cos(x) = 1/2 in the interval [0, 2π).
- Solution:
- Let y = sin(x)cos(x). This is equivalent to:
2y = sin(2x)
- Set up the equation:
sin(2x) = 1
- Since sin(2x) = 1 in [0, 2π), we have:
2x = π/2 + 2kπ
- Solving for x:
x = π/4 + kπ
- Thus, x can be π/4, 5π/4 in [0, 2π).
- Let y = sin(x)cos(x). This is equivalent to:
Using Trigonometry for Problem Solving

Many problems in trigonometry require creative thinking to apply trigonometric concepts in new ways.
- Problem: If sin(A) = 3/5 and cos(A) = -4/5, find sin(2A) and cos(2A).
- Solution:
- Using double-angle formulas:
- sin(2A) = 2sin(A)cos(A) = 2(3/5)(-4/5) = -24/25
- cos(2A) = cos^2(A) - sin^2(A) = (-4/5)^2 - (3/5)^2 = 16/25 - 9/25 = 7/25
- Using double-angle formulas:
Throughout this exploration of trigonometric problems, we've seen how understanding core trigonometric principles can unlock solutions to a wide variety of mathematical challenges. From simplifying expressions to real-world applications, the versatility of trigonometry stands out. By practicing these types of problems, you sharpen your analytical skills and deepen your appreciation for the subject. Remember that trigonometry, like any mathematical discipline, thrives on practice, consistency, and a thorough understanding of its foundational concepts.
Why are trigonometric identities important in solving problems?

+
Trigonometric identities provide a framework for simplifying complex expressions and solving equations involving trigonometric functions. They are fundamental for converting one trigonometric expression into another form that might be easier to solve or understand.
Can trigonometric functions be used in fields outside of mathematics?

+
Yes, trigonometric functions are widely used in physics, engineering, architecture, astronomy, and even in music and audio engineering for analyzing waves and frequencies.
How can I practice trigonometry effectively?

+
Practicing regularly, working through problem sets, understanding the proofs of identities, and applying trigonometric concepts to real-world problems can greatly improve your understanding and proficiency in trigonometry.