5 Steps to Calculate Triangular Prism Volume Easily
Understanding how to calculate the volume of a triangular prism is an essential skill for students and professionals in fields such as engineering, architecture, and design. A triangular prism, with its simple yet intriguing structure, presents a unique opportunity to grasp the basic principles of volume calculation in 3D geometry. In this comprehensive guide, we'll break down the process into five easy steps, ensuring that even those new to this concept can follow along with ease and precision.
What is a Triangular Prism?

A triangular prism is a polyhedron, which means it's a 3D shape with flat sides (faces) that are polygons. Here's what makes it unique:
- It has two parallel triangular bases that are identical in shape and size.
- The sides are rectangles or parallelograms, connecting corresponding sides of the triangular bases.
🎓 Note: Understanding the difference between triangular prisms and other polyhedra can aid in visualizing its properties better.
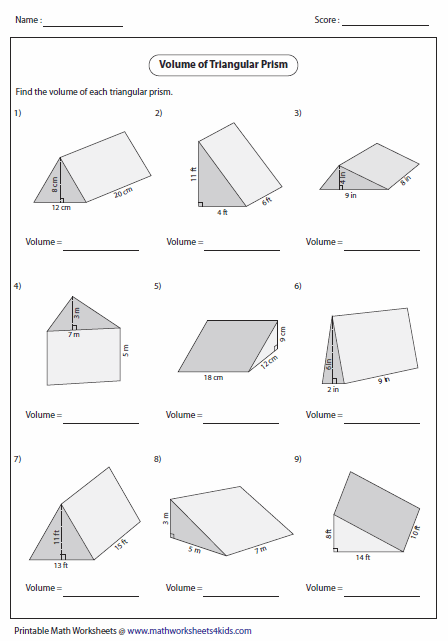
Step 1: Understand the Formula

The volume V of a triangular prism can be calculated using the formula:
\[ V = \frac{1}{2} \times b \times h \times l \]
where:
- b - base of the triangular face.
- h - height of the triangular face (not the height of the prism).
- l - length (or height) of the prism itself.
Here's what you need to remember:
- Since we're dealing with volume, all measurements must be in the same unit, like meters or centimeters.
- The formula essentially multiplies the area of the triangular face by the height of the prism.
Step 2: Identify Measurements

To calculate the volume, you first need to identify the following measurements:
- Base of the triangle: This is the length of the base side of the triangular face. Measure or note down this dimension.
- Height of the triangle: This is the perpendicular distance from the base to the opposite vertex. Make sure to measure perpendicularly.
- Height of the prism: Also known as the length, this is the distance between the two parallel triangular faces.
Step 3: Calculate the Area of the Base

Using the measurements from the previous step, calculate the area of one triangular base:
[ \text{Area of the triangle} = \frac{1}{2} \times b \times h ]
For example, if your base (b) is 4 cm and the height of the triangle (h) is 3 cm, then:
[ \text{Area of the triangle} = \frac{1}{2} \times 4 \times 3 = 6 \text{ square centimeters (cm}^2\text{)} ]
🖌️ Note: Ensuring that you have the correct base and height measurements is crucial as any error can significantly skew your volume calculation.
Step 4: Apply the Prism Height

Now, multiply this area by the height (or length) of the prism:
[ V = \text{Area of the triangle} \times \text{prism height} ]
Continuing with our example, if the height (l) of the prism is 7 cm:
[ V = 6 \times 7 = 42 \text{ cubic centimeters (cm}^3\text{)} ]
Step 5: Volume Calculation Summary

Let's wrap up with the steps:
- Understand the formula: Volume V = \frac{1}{2} \times b \times h \times l .
- Identify measurements: Base, height of the triangle, and height of the prism.
- Calculate the area of the base: Using the formula for the area of a triangle.
- Multiply by the prism height: To get the total volume.
- Review your work: Ensure all dimensions were measured and calculated correctly.
By following these steps, you can easily calculate the volume of any triangular prism. This method simplifies what might initially appear as a complex 3D shape into a manageable calculation.
Here's a quick reference table for our calculation:
| Measurement | Value |
|---|---|
| Base (b) | 4 cm |
| Height of the Triangle (h) | 3 cm |
| Height of the Prism (l) | 7 cm |
| Area of Triangular Base | 6 cm2 |
| Volume of Triangular Prism | 42 cm3 |

The mastery of calculating volumes isn't just about academic knowledge; it's a fundamental skill with practical applications in many fields. Whether you're planning a garden or designing a building, understanding the volume of shapes like the triangular prism can lead to more efficient use of space and materials.
Why is it important to measure the height of the triangle perpendicularly?
+
Measuring the height of the triangle perpendicularly ensures that you get the true perpendicular distance from the base to the opposite vertex, giving you the accurate area for volume calculation.
Can the height of the prism be different from the height of the triangle?

+
Yes, the height of the prism (length) refers to the distance between the two parallel triangular bases, which can be different from the height of the triangle. It’s the distance through which the triangular shape is extended.
What if I only have one triangular face measurement?

+
If you have one triangular face measurement and know that the triangular prism has two identical triangular bases, you can use those measurements. If not, you’ll need to find or measure all necessary dimensions for the calculation.
How do I apply these principles to other prisms?

+
The concept remains the same: find the area of the base (whether it’s triangular, rectangular, or another shape) and multiply it by the height of the prism. The base will vary in shape, but the formula is essentially the same.
What are some practical applications of calculating the volume of a triangular prism?

+
Calculating the volume of a triangular prism is useful in construction for estimating material needs, in engineering for design purposes, and in packaging to determine space utilization efficiently.