7 Triangle Theorems Every Student Should Know

Understanding Triangles: Foundations of Geometry

Triangles are the building blocks of geometry, the most basic geometric shape with fundamental properties that extend to complex mathematical and real-world applications. Mastery over these shapes is crucial for anyone looking to delve deeper into the fascinating world of mathematics or into engineering, architecture, or other related fields. In this blog post, we'll explore seven key triangle theorems that every student should know, understand, and apply.

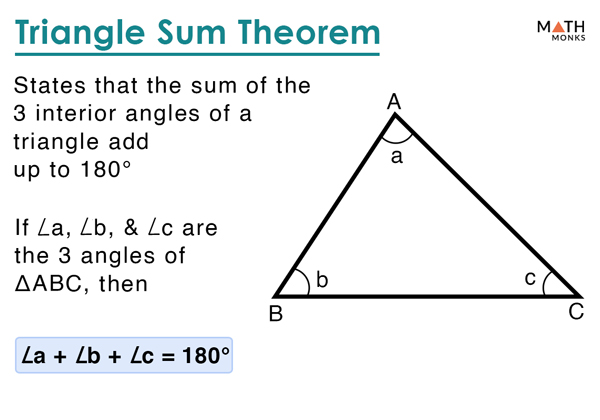
1. The Sum of Interior Angles Theorem

Statement: The sum of the interior angles of a triangle is always 180°.

This theorem is one of the first encountered in geometry because it serves as a fundamental property of triangles. Here's how to visualize it:

• Draw a triangle.
• Make a straight line from one vertex to the midpoint of the opposite side.
• Now, you have created two triangles with angles that sum up to 180°.

🚨 Note: This theorem works for all triangles, regardless of their side lengths or angle types (acute, obtuse, or right).

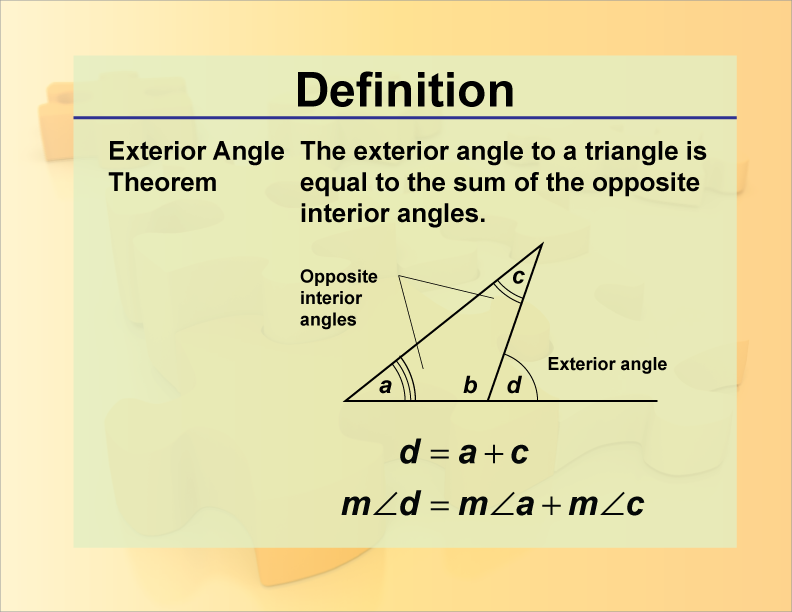
2. The Exterior Angle Theorem

Statement: The measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles.

This theorem helps in understanding how external angles relate to the internal structure of triangles:

• Consider triangle ABC with exterior angle ∠ACD on side BC.
• ∠ACD equals ∠B + ∠C.

🔎 Note: This theorem is particularly useful in angle-chasing problems where you need to find unknown angles.

3. The Congruence Theorems

Understanding triangle congruence is essential for establishing that two triangles are identical in shape and size. Here are the main theorems:

Side-Side-Side (SSS) Congruence

Statement: If three sides of one triangle are equal to three sides of another triangle, the triangles are congruent.

Side-Angle-Side (SAS) Congruence

Statement: If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, the triangles are congruent.

Angle-Side-Angle (ASA) Congruence

Statement: If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, the triangles are congruent.

Angle-Angle-Side (AAS) Congruence

Statement: If two angles and a non-included side of one triangle are equal to two angles and the corresponding non-included side of another triangle, the triangles are congruent.

Right Angle Hypotenuse-Side (RHS) Congruence

Statement: For right-angled triangles, if the hypotenuse and one leg are equal to the hypotenuse and one leg of another right triangle, they are congruent.

A table for quick reference:

Congruence Theorem	Required Conditions
SSS	Three sides equal
SAS	Two sides and included angle equal
ASA	Two angles and included side equal
AAS	Two angles and a non-included side equal
RHS	Right angle, hypotenuse, and one leg equal

🌟 Note: These theorems are fundamental in proving triangle congruence and can be used to solve complex problems in geometry.

4. The Pythagorean Theorem

Statement: In a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

This theorem, often stated as:

\[ a^2 + b^2 = c^2 \]

where a and b are the legs and c is the hypotenuse, is critical for various applications including distance calculation in coordinate geometry:

5. The Midline Theorem

Statement: The segment joining the midpoints of two sides of a triangle is parallel to the third side and half as long.

Here's how to visualize it:

• Identify the midpoints on two sides of a triangle.
• Join these midpoints with a line.
• This line will be parallel to the third side and half its length.

This theorem not only helps in understanding the geometric relationships within a triangle but also has practical applications in engineering, such as dividing land or creating patterns in sewing.

6. The Inscribed Angle Theorem

Statement: The angle subtended by an arc at the center of a circle is twice the angle subtended at any point on the remaining part of the circle.

This theorem, when applied to triangles, relates to the circumscribed circle's properties:

• The inscribed angle formed by two chords of a circle equals half the measure of the arc they subtend.

This theorem is particularly useful in circle-related geometry, but also in understanding how angles in triangles relate to arcs and circles.

7. The Law of Sines and the Law of Cosines

These laws extend the reach of trigonometry into triangle analysis beyond right triangles:

The Law of Sines

Statement: In any triangle, the ratio of the length of a side to the sine of the opposite angle is constant:

[ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} ]

The Law of Cosines

Statement: A generalization of the Pythagorean theorem for any triangle:

[ c^2 = a^2 + b^2 - 2ab\cos C ]

Both laws are invaluable in solving triangles when some sides and angles are known but not all, making them indispensable tools in various mathematical calculations.

Triangles, despite their simple appearance, hold an immense wealth of properties and theorems. Understanding these seven theorems gives a solid foundation in geometry. Whether you're proving the congruence of triangles, calculating distances, or applying trigonometric principles to solve real-world problems, these theorems are the stepping stones to greater geometric insights.

As we've explored, from the fundamental properties to complex relations, triangles provide a rich canvas for mathematical exploration. Their theorems are not merely for academic purposes but are tools in problem-solving, design, and practical applications in numerous fields.