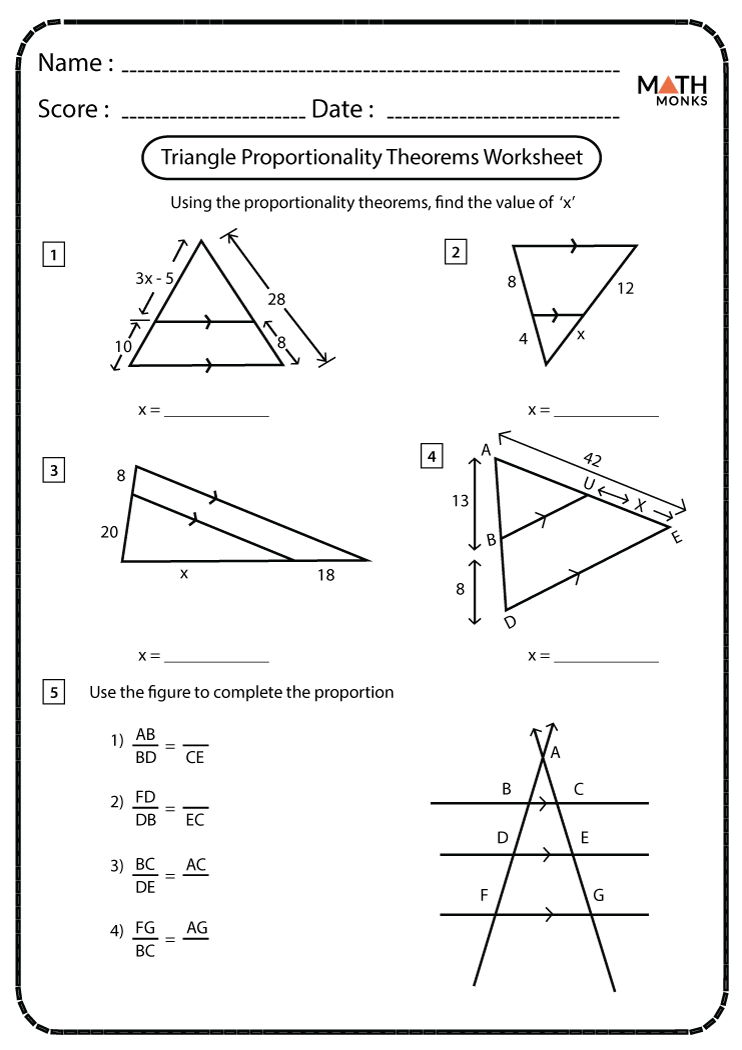
5 Key Answers: Triangle Proportionality Theorem Worksheet

The Triangle Proportionality Theorem, or Thales' Theorem, is a fundamental geometric concept that applies when a line drawn parallel to one side of a triangle divides the other two sides into proportional segments. Understanding this theorem not only enhances your knowledge of geometry but also equips you with skills to solve various mathematical problems. In this extensive blog post, we'll delve into the theorem, how it works, and explore a comprehensive worksheet to master its application.
What is the Triangle Proportionality Theorem?

The Triangle Proportionality Theorem states that if a line is drawn parallel to one side of a triangle to intersect the other two sides, then this line divides those two sides in the same ratio. Mathematically, if in triangle ABC, a line DE is parallel to BC, then:
- DE divides AB in the ratio of AD to DB, and
- DE divides AC in the ratio of AE to EC.
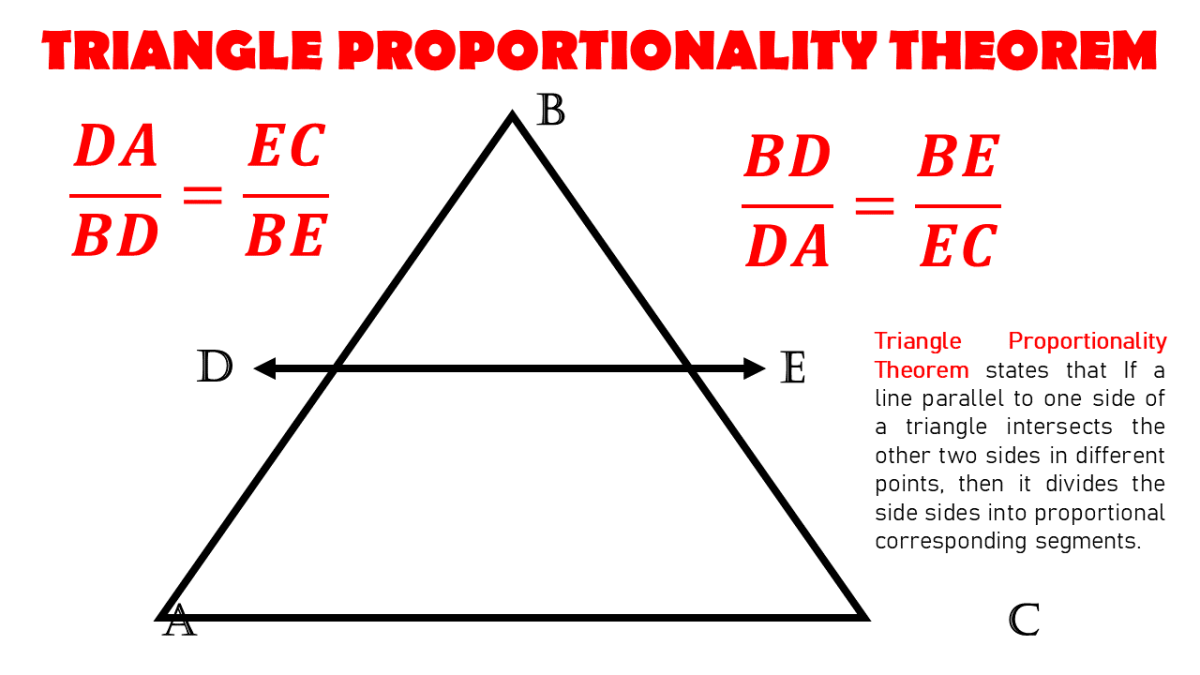
Detailed Explanation of the Theorem
Let's break down the theorem with an example for better understanding:
- Consider triangle ABC with line DE parallel to BC. Here, line DE intersects AB at D and AC at E.
- According to the theorem:
- AD / DB = AE / EC
- This relationship indicates that the ratio of the segments created by line DE on AB and AC will be identical, which is a direct consequence of the similar triangles formed by the parallel line.
Here's a visual representation to aid in understanding:
| Triangle ABC | Line DE | Proportions |
|---|---|---|
| AB | DE || BC | AD / DB = AE / EC |
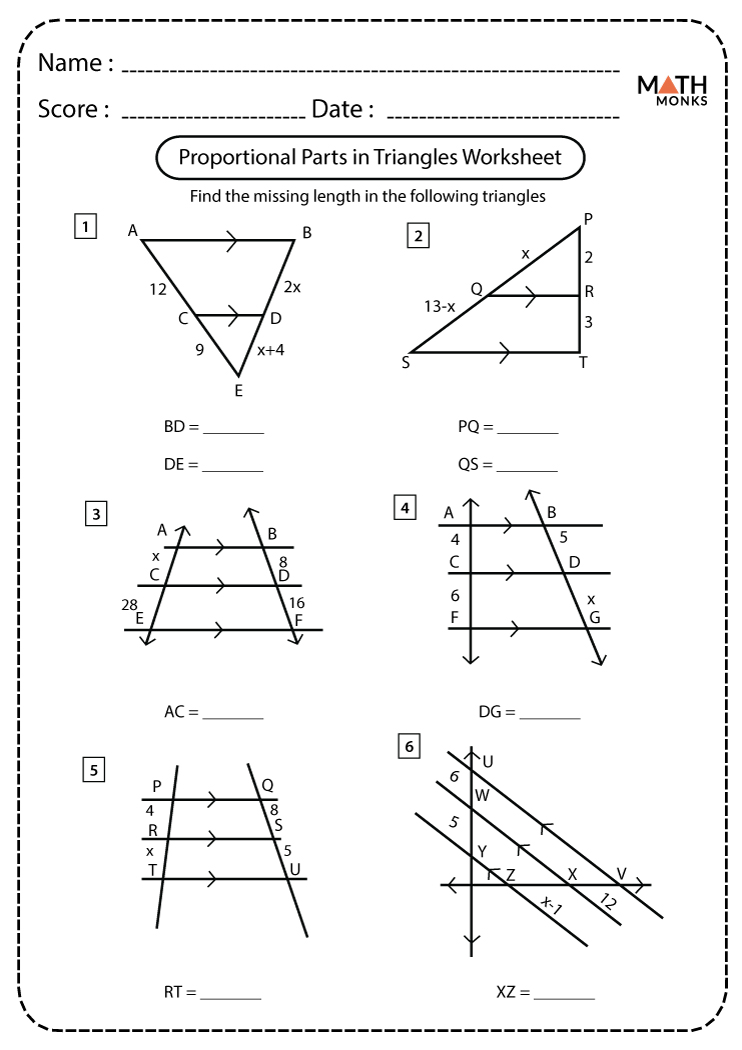
Worksheet on Triangle Proportionality Theorem

To master the application of the Triangle Proportionality Theorem, let's go through some exercises:
Problem 1: Given Proportions

Given triangle ABC with BC parallel to DE, AD = 4, DB = 6, and AE = 5. Find EC.
- Using the theorem, we know:
- AD / DB = AE / EC
- 4 / 6 = 5 / EC
- 4EC = 30
- EC = 7.5
Problem 2: Angle Calculation

If triangle XYZ has a line parallel to one side, dividing it into segments where the ratio of the segments is 2:3, what is the relationship between the angles at the intersection of this parallel line with the triangle?
- The angles at these points will correspond to the original angles due to the Alternate Interior Angles Theorem.
Problem 3: Finding Lengths

In triangle ABC, a line DE is parallel to BC, and it divides AB into segments AD = 3 cm and DB = 9 cm. If AC is 18 cm, find AE.
- AD / DB = AE / EC
- 3 / 9 = AE / (18 - AE)
- After solving, AE = 4.5 cm
Key Takeaways

- The Triangle Proportionality Theorem is a direct application of similar triangles.
- When a line is parallel to one side of a triangle, it creates two pairs of similar triangles.
- Understanding and applying this theorem allows for solving geometric problems involving proportions, lengths, and angles.
📝 Note: Remember, in practical problems, it's crucial to verify that the given conditions align with the theorem's prerequisites (e.g., ensuring the line is truly parallel).
📝 Note: The converse of the Triangle Proportionality Theorem also holds true: if a line divides two sides of a triangle into proportional segments, then that line is parallel to the third side.
📝 Note: This theorem has broad applications in trigonometry, coordinate geometry, and even in fields like engineering for scaling and proportion analysis.
In wrapping up this exploration of the Triangle Proportionality Theorem, we've covered its statement, practical application through a worksheet, and some key considerations. Understanding this theorem not only sharpens your geometric skills but also opens doors to understanding complex geometric relations and their applications in real-world scenarios. By practicing these problems and recognizing the theorem in various contexts, you'll develop a deeper intuition for how proportions govern the harmony of shapes and structures in both mathematics and the world around us.
How do I know if a line is parallel to one side of a triangle?
+
Look for corresponding angles, alternate interior angles, or any other parallel line properties. If these angles are equal or complementary, the line is likely parallel.
Can the Triangle Proportionality Theorem be applied to non-isosceles triangles?

+
Yes, the theorem applies to any triangle as long as a line is drawn parallel to one side, intersecting the other two.
What if the line doesn’t divide both sides proportionally?

+
If the line doesn’t divide both sides proportionally, it might not be parallel to the base side of the triangle, or the conditions of the theorem aren’t met.