Triangle Proportionality Theorem: Fun Worksheet and Tips

Are you looking for an engaging way to understand or teach the Triangle Proportionality Theorem? Often tucked away in the middle of geometry textbooks, this theorem is not only crucial for solving triangle problems but also offers some fun applications in real life. This blog post will guide you through the theorem with a delightful worksheet and provide handy tips to master this concept effortlessly.

What is the Triangle Proportionality Theorem?

The Triangle Proportionality Theorem states that if a line parallel to one side of a triangle intersects the other two sides, then it divides those sides proportionally. Simply put, if you draw a line through a triangle parallel to its base, the segments it creates on the other sides will be in proportion.

Here's how it mathematically works:

• Consider a triangle ABC.
• A line DE is drawn parallel to the base BC, intersecting AB at D and AC at E.
• The theorem claims that AD/DB = AE/EC.

Understanding Through a Fun Worksheet

Here's a worksheet tailored to make learning the Triangle Proportionality Theorem interactive and fun:

Triangle Proportionality Theorem Worksheet

📝 Note: These problems can be easily solved using the proportions we've discussed. Remember, the key is setting up the proportion correctly.

Steps to Solve Problems Using the Theorem

Here’s a step-by-step guide to apply the Triangle Proportionality Theorem:

1. Identify the sides involved: Look for the sides of the triangle that are intersected by the parallel line.
2. Set up the proportion: Based on the theorem, if line DE is parallel to BC, then AD/DB = AE/EC.
3. Cross-multiply to solve: Using the proportion, you can cross-multiply to find the unknowns. For example, if AD = x, DB = 10 - x, AE = 4, and EC = 6, then you set up the equation (x / (10 - x)) = 4/6.
4. Simplify the equation: Solve for the unknown by simplifying the proportion. In our example, x = 5.
5. Check your solution: Verify your answer by substituting the found value back into the problem.

📊 Note: Always label your triangle clearly and ensure that your proportions reflect the correct segments.

Real-Life Applications of the Theorem

While it might seem like an abstract concept, the Triangle Proportionality Theorem has real-life applications:

• Architecture: Understanding proportions helps architects maintain visual harmony and structural integrity in their designs.
• Landscaping: Garden designers use this theorem to layout paths or structures in proportion to the surrounding area.
• Photography: Photographers apply proportions to ensure balance in their compositions, especially when capturing landscapes or buildings.

🌿 Note: While direct applications might be subtle, the principles of proportionality are ubiquitous in design and nature.

Tips for Teaching or Learning the Theorem

To make the learning process smoother:

• Use Visual Aids: Draw triangles and parallel lines on a whiteboard or use geometric software to demonstrate the theorem visually.
• Practice with Real-World Examples: Find images or scenarios where the theorem can be applied, like road signs or flagpole shadows.
• Incorporate Technology: Interactive tools like GeoGebra can provide a dynamic understanding of how changing angles or lengths affects proportions.
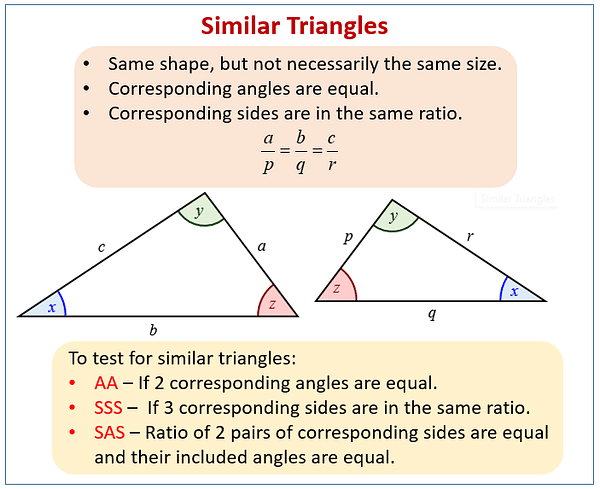
• Relate to Similar Triangles: Explaining that parallel lines create similar triangles can help solidify the concept.
• Group Activities: Encourage collaborative problem-solving where students can explain the theorem to each other.

By grasping this theorem, students can open doors to more complex geometric relationships and real-life problem-solving skills.

💡 Note: Encouraging active learning through discussions and group work can significantly enhance understanding.

In summary, the Triangle Proportionality Theorem isn't just a formula; it's a bridge to understanding the beauty of symmetry in mathematics and the real world. Whether you're a teacher looking to engage students or a student eager to excel in geometry, the worksheet provided, along with the tips, will help you navigate this theorem with ease. Remember, the key to mastering it lies in visualizing the theorem in action and applying it creatively to solve problems.

Can the Triangle Proportionality Theorem be applied to non-equilateral triangles?

+

Yes, the theorem applies to any triangle, regardless of whether it’s equilateral, isosceles, or scalene, as long as the line is parallel to one of its sides.

What if the line isn’t perfectly parallel to the base?

+

If the line isn’t parallel to the base, the theorem does not hold. The segments created would not be proportional, but you could explore other geometric properties like angles or non-proportional relationships.

How does this theorem relate to similar triangles?

+

The line that’s parallel to one side of a triangle creates two similar triangles with the larger triangle. This relationship is key to understanding why the segments created are proportional.

This comprehensive guide has provided you with an overview, practical applications, and teaching tips for the Triangle Proportionality Theorem. By engaging with the interactive worksheet and following the steps outlined, you’ll find this once perplexing theorem becomes a clear and logical piece of geometry you can apply in various contexts. Remember to incorporate visual learning, practice regularly, and make connections to real-world applications to keep the learning process engaging and relevant.