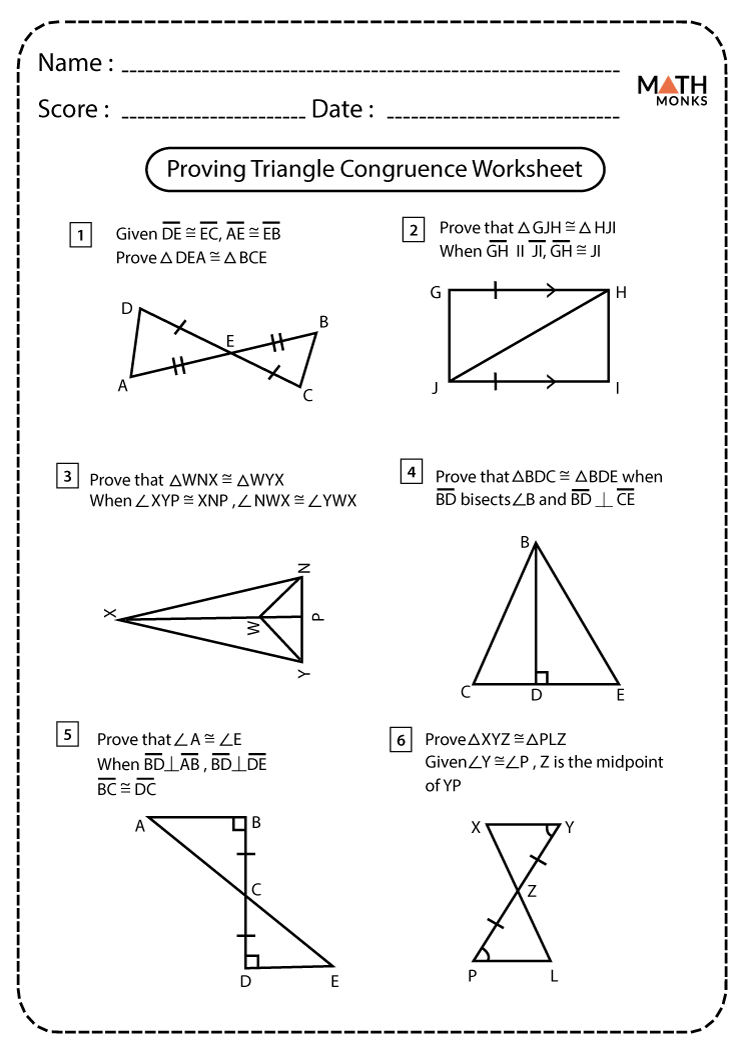
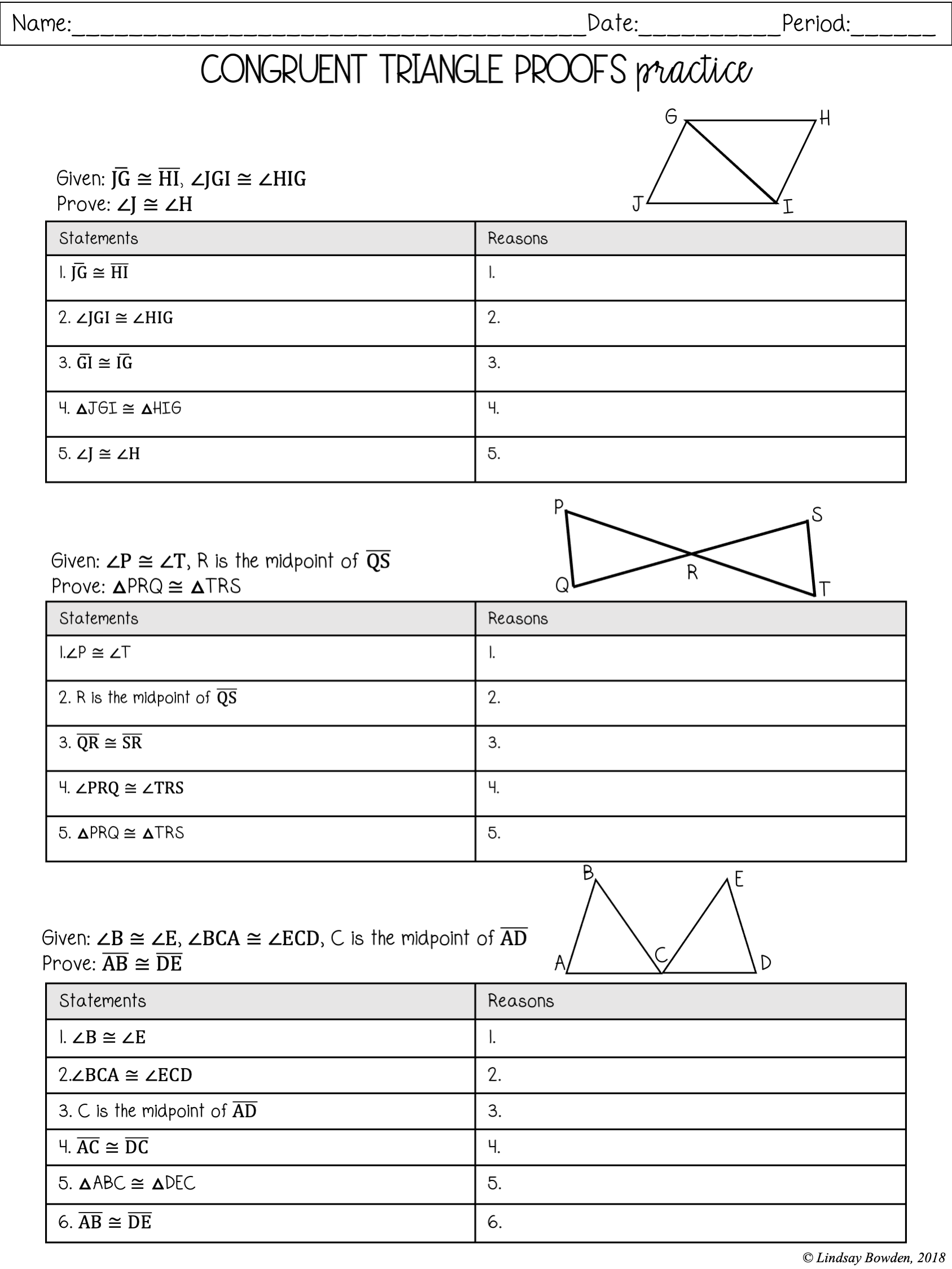
Triangle Proofs Worksheet: Easy Answers for Quick Learning

If you've ever tried to prove a triangle property or theorem, you'll know that it often involves intricate steps and logical reasoning. Whether you're learning about triangle properties for the first time or looking to refresh your memory, understanding these proofs can help deepen your mathematical intuition and problem-solving skills. Let's dive into some easy triangle proofs with a focus on concise explanations and quick learning techniques.
Understanding Basic Triangle Properties

Before delving into proofs, it’s crucial to understand some fundamental properties of triangles:
- The sum of the angles in any triangle is 180 degrees.
- Any side of a triangle must be shorter than the sum of the other two sides (Triangle Inequality Theorem).
- The interior angles of a triangle are formed where two sides meet, and the exterior angles are formed outside the triangle with one side of the triangle.

📖 Note: Understanding these properties is essential before attempting to prove theorems involving triangles.
Proving the Triangle Sum Theorem

The Triangle Sum Theorem states that the three interior angles of a triangle always sum to 180 degrees. Here’s a simple way to prove this:
- Draw any triangle.
- Extend one of the sides to form a straight line.
- Now, you have a straight line with an exterior angle that forms a linear pair with one of the triangle's interior angles. This exterior angle is equal to the sum of the other two interior angles.
- Since a straight line (or a linear pair of angles) measures 180 degrees, and it includes one of the interior angles, the remaining two interior angles must also sum to 180 degrees minus that angle.
| Step | Description |
|---|---|
| 1 | Draw a triangle and extend one side to form a straight line. |
| 2 | Identify the exterior angle created by this extension. |
| 3 | Use the fact that the exterior angle equals the sum of the opposite interior angles. |
| 4 | Conclude that the sum of all three angles is 180 degrees. |


📝 Note: This proof is foundational and often used in more complex geometric proofs.
Proving the Exterior Angle Theorem
The Exterior Angle Theorem tells us that an exterior angle of a triangle is equal to the sum of the two remote (non-adjacent) interior angles. Here’s how you can prove this:
- Consider any triangle.
- Extend one side to create an exterior angle.
- Mark the exterior angle as A and the two non-adjacent interior angles as B and C.
- The interior angles of a triangle sum up to 180 degrees. Since A is formed by the straight line and one of the interior angles, A + interior angle = 180 degrees.
- Thus, A = 180 degrees - interior angle. The interior angle is part of the triangle's 180 degrees sum, so A = B + C.
Using Basic Proofs for Advanced Concepts

Once you have these basic proofs in your toolkit, you can tackle more advanced triangle properties:
- Prove the Pythagorean Theorem.
- Explore properties of right-angled triangles.
- Understand the congruence criteria like Side-Side-Side (SSS), Side-Angle-Side (SAS), etc.
The Importance of Visualization

Visualizing triangle properties and proofs can significantly aid your understanding:
- Use diagrams to help visualize angles and sides.
- Color-coding different parts of the triangle can help identify relationships between angles.
🎨 Note: Visualization is not just about seeing, but also about thinking critically about what you see.
Strategies for Quick Learning
Here are some strategies to speed up your learning of triangle proofs:
- Draw your proofs: Sketching diagrams helps in visualizing the relationship between angles and sides.
- Start with simpler cases: Understand simple proofs first, then build on your knowledge.
- Practice with real-world applications: Apply triangle properties to real-life situations like navigation, architecture, and engineering.
- Use mnemonic devices: Develop memory aids for theorems and proofs.
As you grow familiar with these proofs and properties, you'll find that your understanding of triangles not only becomes more profound but also more applicable to other areas of mathematics. The systematic approach to triangle proofs will refine your logical thinking and help in tackling more complex geometric challenges.
Why are triangle proofs important in geometry?

+
Triangle proofs are foundational because they help establish the logical framework for understanding and proving other geometric properties and theorems.
How can I remember the steps of triangle proofs?

+
Using mnemonic devices, visual aids, and practicing the proofs repeatedly can help you remember the steps more effectively.
Can triangle proofs be applied outside of geometry?

+
Yes, the logical reasoning behind triangle proofs can enhance critical thinking skills applicable in various disciplines like engineering, computer science, and physics.