5 Proven Strategies for Triangle Proofs Mastery

Delving into the world of geometry, particularly the realm of triangle proofs, often seems daunting at first glance. Yet, mastering these proofs is a fundamental part of understanding and applying geometrical concepts. Whether you're a student trying to conquer the next math exam or an enthusiast looking to deepen your understanding, here are five proven strategies to help you achieve triangle proofs mastery.
Strategy 1: Understand the Basics of Triangles


Before diving into triangle proofs, ensure you have a solid grasp of:
- Types of Triangles: Equilateral, Isosceles, Scalene, Right, Acute, and Obtuse.
- Angles: Understanding the sum of angles, complementary, supplementary, and opposite angles.
- Sides: Congruent sides and inequalities related to triangle sides.
Once you understand these foundational elements, you'll be better equipped to tackle proofs involving triangles.
Strategy 2: Master Fundamental Proof Techniques

Here are some essential proof techniques for mastering triangle proofs:
- Direct Proof: Start with known information and logically derive the conclusion.
- Proof by Contradiction: Assume the opposite of what you want to prove and show that this assumption leads to an absurdity or contradiction.
- Indirect Proof: Similar to contradiction, but you prove the statement by proving the contrapositive.
📝 Note: Practicing different types of proofs will enhance your flexibility in approaching any triangle proof problem.
Strategy 3: Utilize Properties and Theorems

Equip yourself with knowledge about key theorems:
| Theorem | Description |
|---|---|
| Pythagorean Theorem | In a right triangle, the square of the length of the hypotenuse is equal to the sum of squares of the other two sides. |
| Congruence Theorems | Understand and use SAS, ASA, SSS, and AAS congruence criteria. |
| Similar Triangles | Identify triangles that are similar by AA, SAS, and SSS similarity criteria. |

Regularly using these properties in your practice sessions will make recalling them during proofs almost second nature.
Strategy 4: Regular Practice with Real Problems

Theoretical knowledge must be complemented with:
- Solving Various Problem Sets: Engage with textbooks, online resources, or worksheets containing different proof problems.
- Analyze Examples: Look at worked examples, understanding each step in the proof process.
- Create Your Own Proofs: Attempt to prove statements without looking at answers. This builds your logical reasoning skills.
✏️ Note: Building a library of solved proofs can serve as a reference point for future challenges.
Strategy 5: Develop a Structured Approach to Proof Writing

Here are steps to structure your approach:
- Read the Problem Carefully: Understand what needs to be proved.
- Draw a Diagram: A visual representation can often clarify the problem.
- List Given Information: Write down all known facts.
- Choose a Proof Strategy: Decide whether you’ll use direct proof, contradiction, or another method.
- Work Through the Steps: Detail each step logically, using properties and theorems as needed.
- Verify Your Proof: Review your work to ensure all steps are logical and no assumptions are made.
With these strategies, you'll not only enhance your ability to prove geometric statements but also gain a deeper appreciation for the beauty of mathematics itself. The key is to practice consistently, build upon your knowledge step by step, and continuously refine your problem-solving approach. Remember, mastering triangle proofs is a journey of continuous learning and understanding geometric relationships.
What is the quickest way to identify similar triangles?
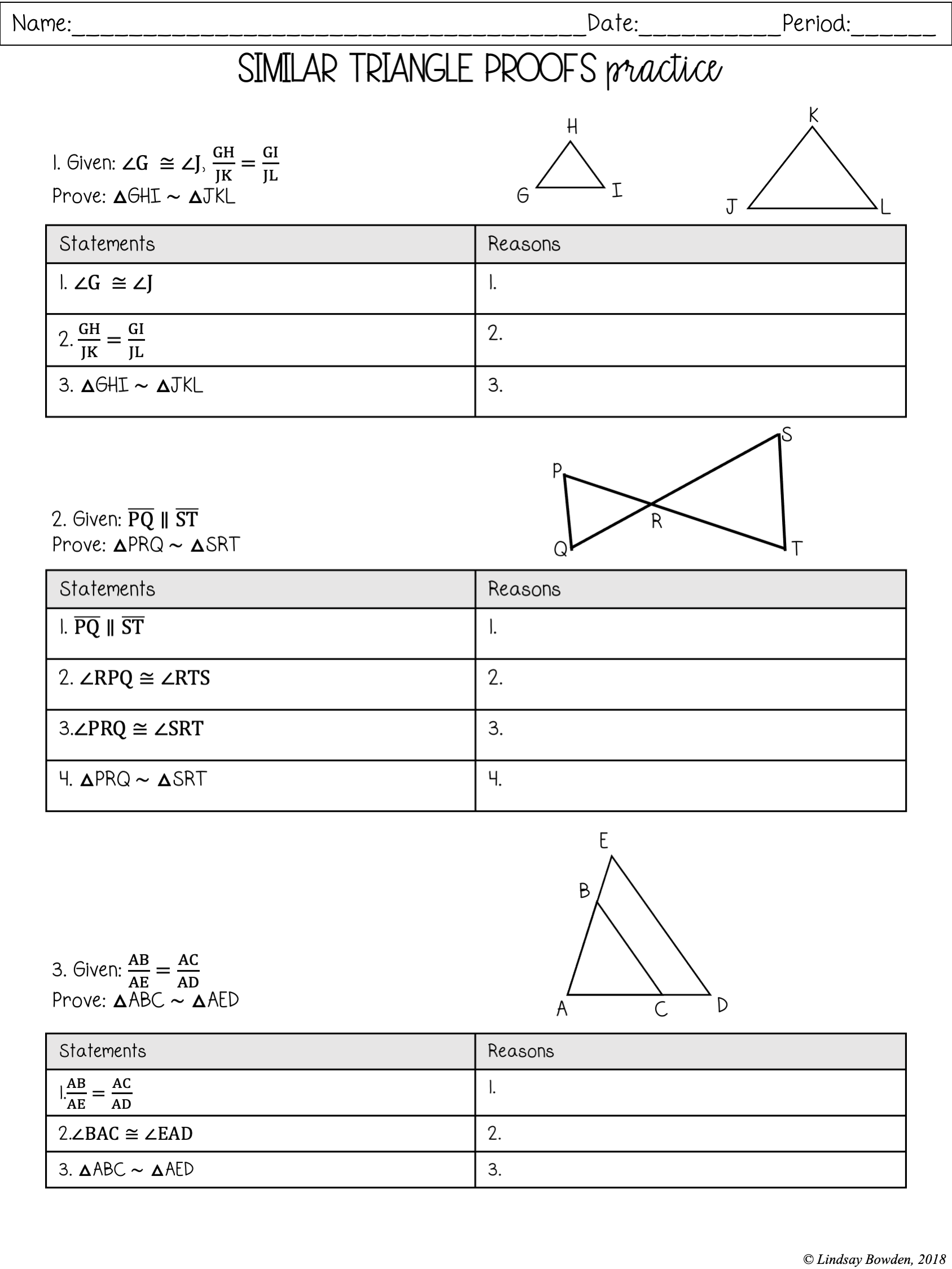
+
The quickest way often involves checking for Angle-Angle (AA) similarity. If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar.
How do I know if a triangle is congruent?

+
Triangles can be proven congruent through Side-Angle-Side (SAS), Angle-Side-Angle (ASA), Side-Side-Side (SSS), or Angle-Angle-Side (AAS) criteria.
Can you recommend resources for practicing triangle proofs?

+
Excellent resources include geometry textbooks like “Geometry: Seeing, Doing, Understanding” by Harold R. Jacobs, online platforms like Khan Academy, and dedicated geometry practice apps.