Triangle Inequality Theorem Worksheets for Quick Mastery

Understanding the Triangle Inequality Theorem
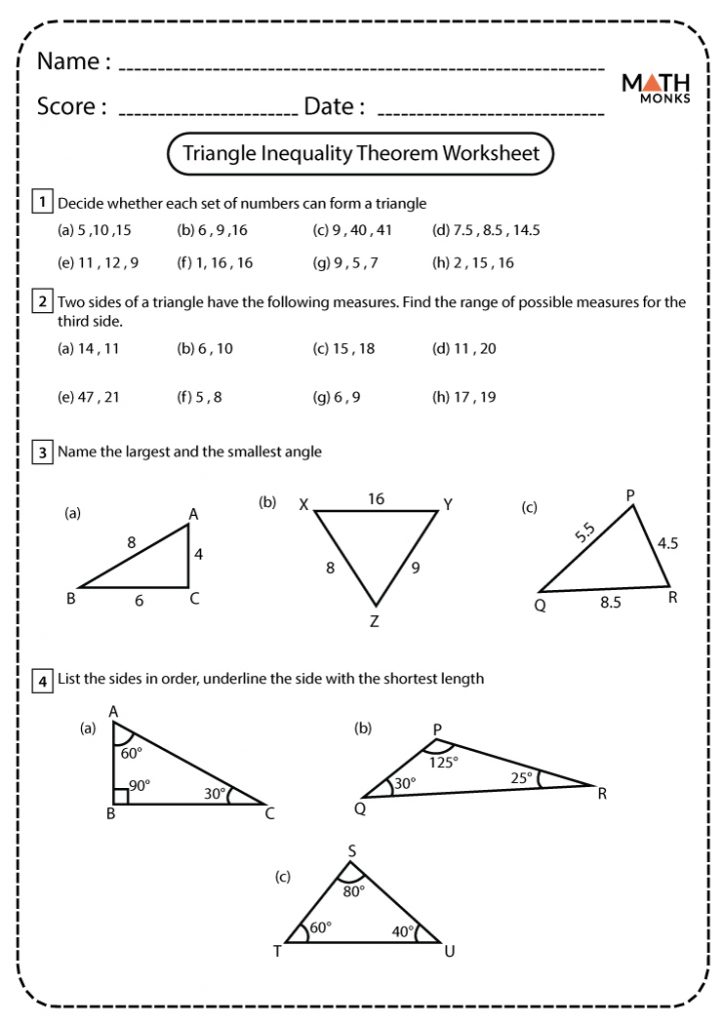
The Triangle Inequality Theorem is a fundamental principle in the study of geometry, particularly when learning about the properties and behaviors of triangles. This theorem provides essential insights into whether three lengths can form a valid triangle, laying down a simple yet crucial rule for triangle construction.
Here's how the theorem is stated:
- The sum of the lengths of any two sides of a triangle must be greater than the length of the remaining side.
This rule must be followed by all sets of three line segments for them to form a triangle. Let's dive into how this theorem is applied, why it's important, and how we can use Triangle Inequality Theorem worksheets to master this concept.
The Importance of the Triangle Inequality Theorem

The Triangle Inequality Theorem isn't just an abstract concept; it has practical applications:
- Geometry and Design: Engineers and architects use this theorem to ensure that structures are stable, ensuring that the sides of triangular components can support each other.
- Computing and Algorithms: It's used in algorithms for tasks like pathfinding, where ensuring paths form valid angles is necessary for efficient solutions.
- Physics: Forces and distances in physical systems can sometimes be analyzed through triangle configurations, where this theorem ensures stability.
Why Worksheets Are Beneficial

Worksheets specifically designed for the Triangle Inequality Theorem offer several advantages:
- Practice: Regular problem-solving helps solidify understanding and familiarity with the theorem.
- Visual Reinforcement: Worksheets often include diagrams, making it easier to visualize and remember the concept.
- Immediate Feedback: Typically, worksheets provide the opportunity to check answers, aiding in learning from mistakes.
- Varied Practice: They cover different scenarios, ensuring learners are prepared for a range of problems.
- Consistent Review: Regularly working through worksheets reinforces the theorem over time.
Types of Triangle Inequality Theorem Worksheets

To cater to various learners, worksheets come in different formats:
1. Fill in the Blank Worksheets

These require students to determine if given side lengths can form a triangle, filling in “Yes” or “No” based on the theorem:
| Side 1 | Side 2 | Side 3 | Can Form a Triangle? |
|---|---|---|---|
| 3 | 4 | 5 | |
| 1 | 1 | 3 |

🌟 Note: Remember, for a set of lengths to form a triangle, each pair must add up to more than the length of the third side.
2. Problem-Solving Worksheets

These challenge learners to solve problems where they must apply the theorem:
- Given side lengths, find all possible integer values for the third side.
- Calculate the range of possible lengths for one side when two sides are provided.
3. Proof-Based Worksheets

These encourage students to prove why the Triangle Inequality Theorem is true using geometric properties or inequalities.
4. Interactive Worksheets

Utilizing online tools or manipulatives, these allow for dynamic exploration and immediate feedback.
5. Error Detection Worksheets

Here, students must identify and correct errors in given triangle configurations or statements related to the theorem.
How to Use Triangle Inequality Theorem Worksheets Effectively

To maximize the benefits from these worksheets:
- Start Simple: Begin with basic problems to ensure the foundation is solid before moving to complex scenarios.
- Visualize: Use diagrams or manipulatives to aid in understanding the concept.
- Group Study: Learning in pairs or small groups can promote discussion and problem-solving skills.
- Use Mixed Practice: Engage with various types of worksheets to cover different aspects of the theorem.
- Self-Check: Always verify answers to learn from mistakes.
- Track Progress: Keep a record of your improvement over time.
💡 Note: If you're struggling with any part of the worksheet, don't hesitate to go back to basics or use resources like geometry software for additional visualization.
Summary of Key Points

The Triangle Inequality Theorem is a cornerstone of geometry, guiding the creation and analysis of triangles. Through consistent practice with specialized worksheets, students gain a deep understanding of this theorem, enhancing their problem-solving skills and geometric intuition. By integrating different types of worksheets into their learning routine, they ensure comprehensive coverage of the theorem's applications, making complex problems feel manageable. Remember, mastering the Triangle Inequality Theorem opens up a world of geometric exploration, paving the way for advanced mathematical concepts and real-world applications.
What is the Triangle Inequality Theorem?

+
The Triangle Inequality Theorem states that for any triangle, the sum of the lengths of any two sides must be greater than the length of the remaining side. If A, B, and C are the lengths of the sides, then A + B > C, A + C > B, and B + C > A.
Why are worksheets important for learning the Triangle Inequality Theorem?
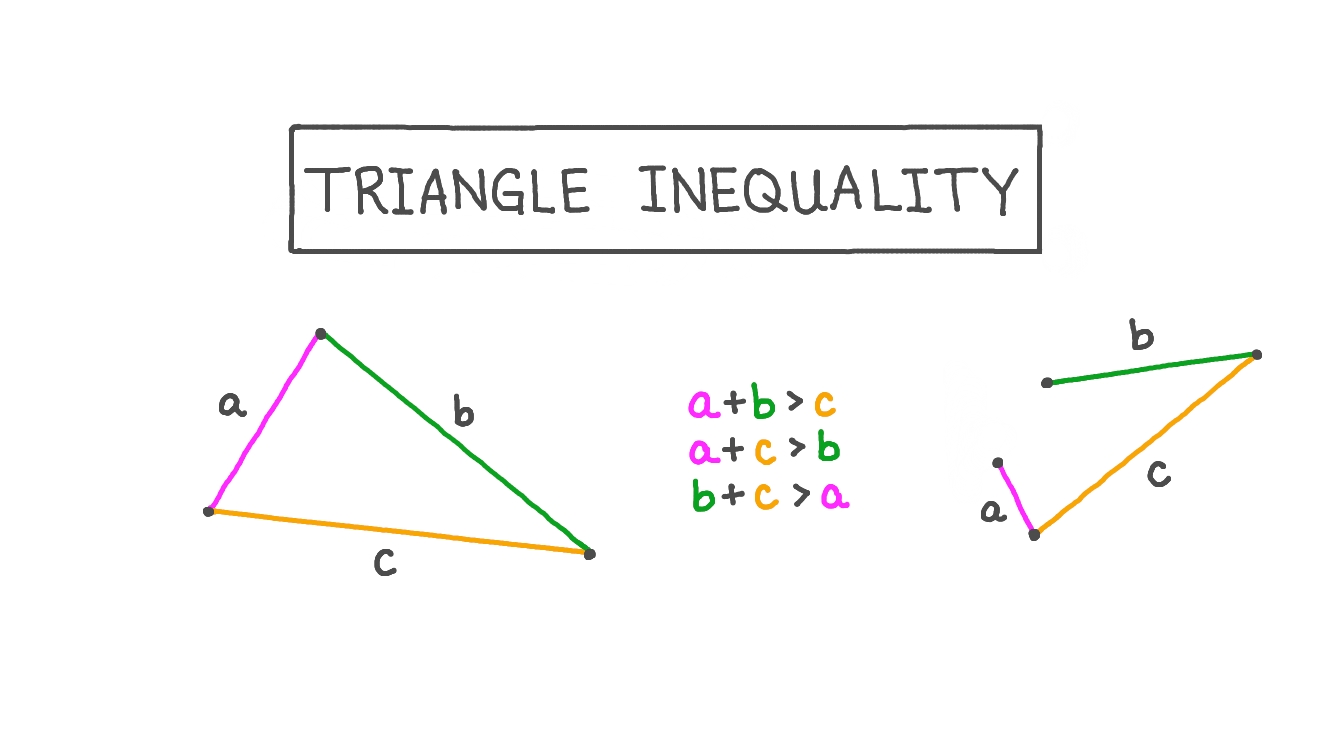
+
Worksheets provide structured practice that reinforces understanding. They promote conceptual clarity through problem-solving, offer visual reinforcement through diagrams, and allow for immediate feedback on errors, facilitating a deeper understanding of the theorem.
Can I use worksheets for other geometry concepts?
+
Yes, worksheets are incredibly versatile tools for learning. You can find or create worksheets on various geometry topics, such as angle properties, congruence, similarity, and even proofs, enhancing your understanding of different mathematical concepts.
How often should I practice with Triangle Inequality Theorem worksheets?

+
Regular practice is key to mastering any concept. Start with shorter, more frequent sessions and gradually increase the complexity and length of your practice as your understanding grows. Consistency over time yields better results than cramming.
Where can I find Triangle Inequality Theorem worksheets?

+
Many educational websites offer free downloadable worksheets, or you can create your own with the guidance of math education resources. Ensure they align with your learning objectives or curriculum.