Triangle Inequality Theorem: Practice Problems and Answers

The Triangle Inequality Theorem stands as a fundamental rule in Euclidean geometry, offering insight into the potential formation of triangles based on the lengths of their sides. This theorem is not just a statement of possibility but a guiding principle that helps in understanding the characteristics of triangles. Let's delve into the intricacies of this theorem, provide practical examples, and explore why understanding it is crucial for anyone studying geometry or solving geometric problems.
What is the Triangle Inequality Theorem?

The Triangle Inequality Theorem states that for any triangle, the sum of the lengths of any two sides must be greater than the length of the remaining side. Mathematically, for a triangle with sides of lengths a, b, and c, where a, b, and c are positive numbers:
- a + b > c
- a + c > b
- b + c > a
📌 Note: If any of these conditions are not met, it's impossible to construct a triangle with those side lengths.
Why is the Triangle Inequality Theorem Important?
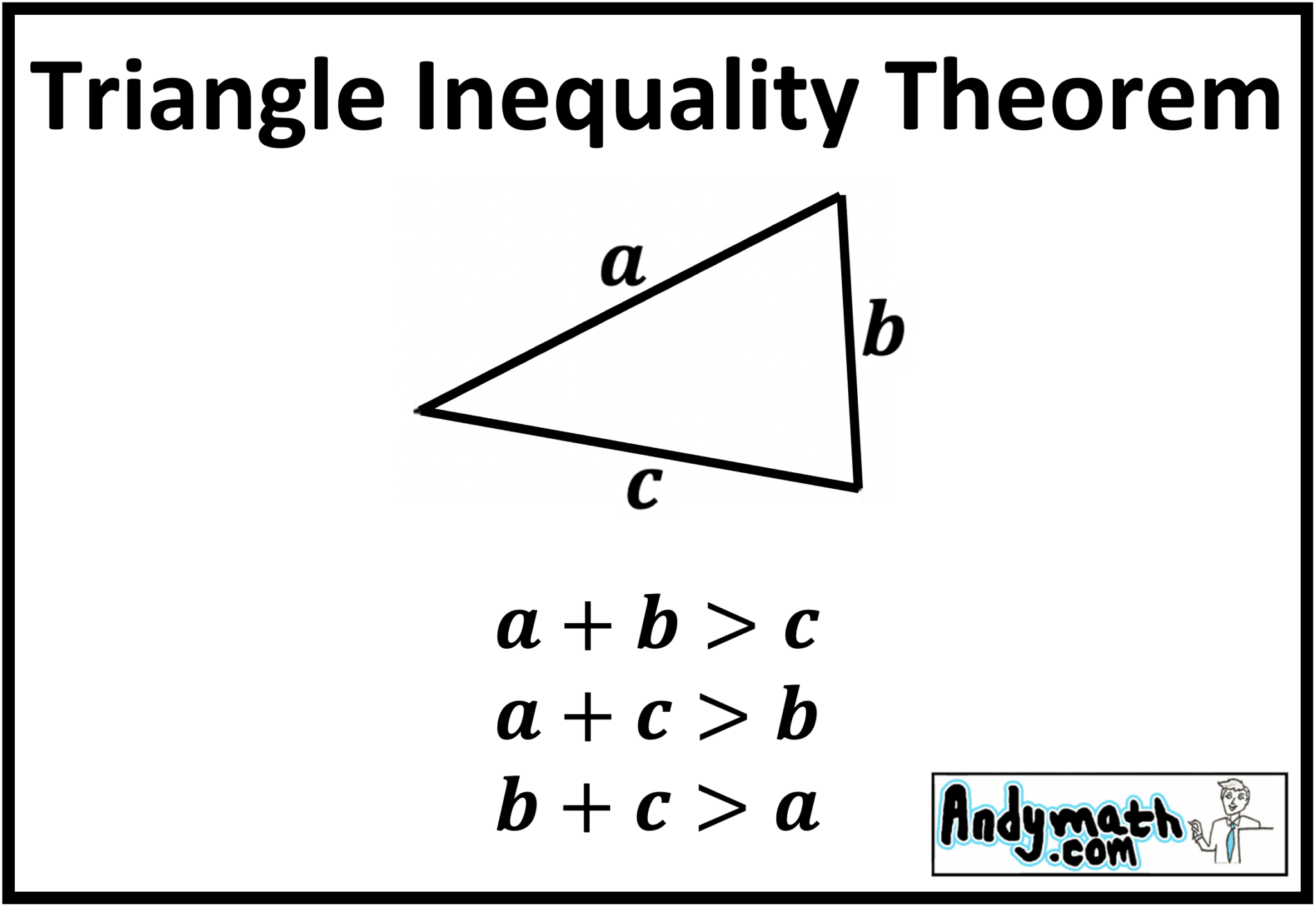
The theorem provides:
- Verification: A quick way to check if a set of side lengths can form a triangle.
- Understanding Triangle Stability: It shows that the sides of a triangle must be balanced in a certain way to maintain the structure's integrity.
- Applications in Real World: From architecture to engineering, this theorem is used to design structures that are stable and functional.
How to Apply the Triangle Inequality Theorem?

Here's a simple process to apply the theorem:
- List the side lengths of the triangle as a, b, and c.
- Check if a + b > c.
- Then verify a + c > b.
- Lastly, ensure b + c > a.
- If all inequalities are true, the sides can form a triangle.
📌 Note: These conditions must be true for any combination of sides to ensure triangle formation.
Practice Problems and Solutions

Problem 1

Can the sides of a triangle be 3, 4, and 8 units?
| Side | Length | Is it valid? |
|---|---|---|
| A | 3 | 3 + 4 = 7 > 8? No |
| B | 4 | 3 + 8 = 11 > 4? Yes |
| C | 8 | 4 + 8 = 12 > 3? Yes |

Since one of the conditions (A + B > C) fails, these side lengths cannot form a triangle.
Problem 2

Check if a triangle with sides of 6, 8, and 10 units is possible.
- 6 + 8 = 14 > 10 ? Yes
- 6 + 10 = 16 > 8 ? Yes
- 8 + 10 = 18 > 6 ? Yes
Since all conditions are met, these side lengths can form a triangle.
Problem 3

Can a triangle be formed with sides of 5, 6, and 12?
- 5 + 6 = 11 > 12? No
- 5 + 12 = 17 > 6? Yes
- 6 + 12 = 18 > 5? Yes
Since one condition fails, these lengths cannot form a triangle.
📌 Note: Remember, all three conditions must be met for a triangle to be valid.
By working through these problems, one can better understand the application of the Triangle Inequality Theorem, enabling them to make accurate predictions about triangle formations and to enhance their problem-solving skills in geometry.
Exploring Further
Beyond basic triangle verification, this theorem can be used in:
- Triangle Classification: Helping to classify triangles into scalene, isosceles, or equilateral based on side lengths.
- Construction and Design: In real-world applications, ensuring the stability and design of triangular structures like trusses, bridges, and frames.
In conclusion, understanding the Triangle Inequality Theorem not only deepens one's appreciation for the elegance of geometry but also equips them with practical knowledge for various applications. By practicing these problems and understanding the theory behind them, students and professionals alike can solve complex geometric problems more efficiently and confidently.
What are some common mistakes when applying the Triangle Inequality Theorem?

+
Common mistakes include: not checking all three conditions, incorrectly summing sides, and using the theorem to determine which triangle type a set of sides will form.
Can the triangle inequality be applied to non-planar geometries?

+
Yes, the principle of triangle inequality exists in other geometries like spherical and hyperbolic geometry, but with modified rules based on the curvature of the space.
How can one remember the Triangle Inequality Theorem easily?

+
An easy mnemonic could be: “The sum of any two must be more than the third”. Additionally, practicing visual examples can help in understanding the spatial implications of the theorem.
Can the Triangle Inequality Theorem help in understanding other geometric shapes?

+
Yes, the principles behind the theorem can extend to polygons where one needs to ensure that the sum of non-adjacent sides must exceed the length of a side to maintain shape stability.