5 Ways to Solve Triangle Congruence Proofs Easily

When it comes to geometry, proving that two triangles are congruent can be both fascinating and somewhat intimidating for many students. Understanding triangle congruence is fundamental to solving many geometric problems and enhancing one's spatial reasoning. Let's delve into five effective methods to make triangle congruence proofs easier and more intuitive.
Understand the Basic Congruence Postulates
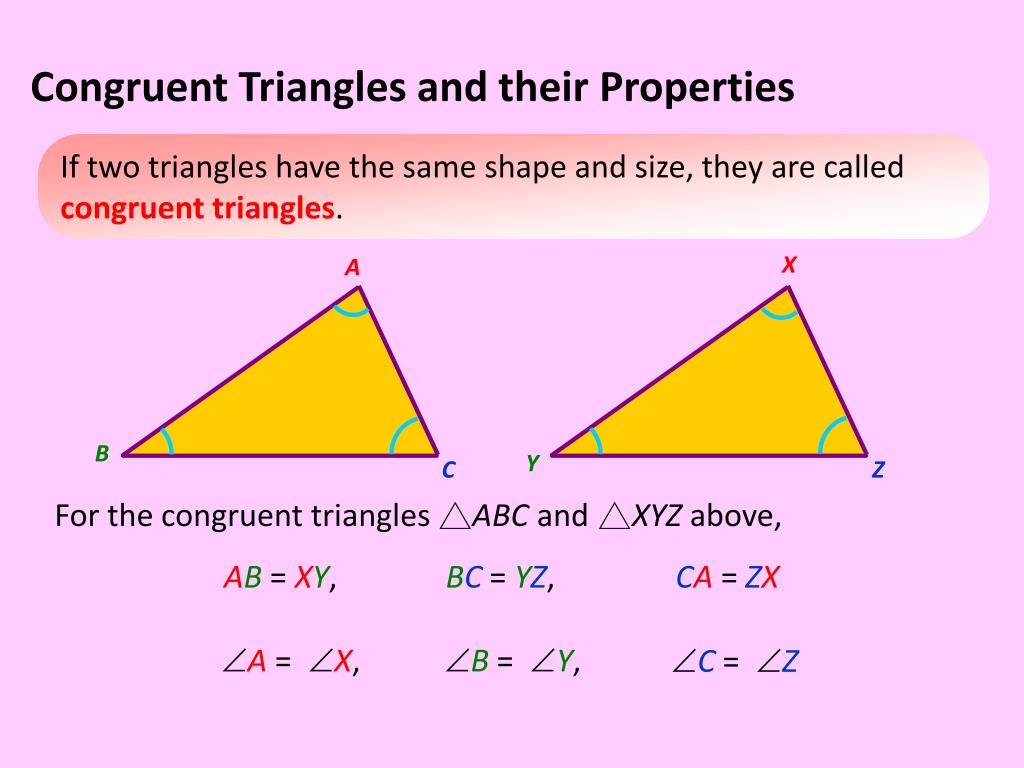
Before we delve into specific strategies, it’s crucial to have a firm grasp of the basic postulates that underpin triangle congruence:
- Side-Side-Side (SSS): If all three sides of one triangle are congruent to the corresponding sides of another triangle, then the triangles are congruent.
- Side-Angle-Side (SAS): If two sides and the included angle of one triangle are congruent to two sides and the included angle of another, the triangles are congruent.
- Angle-Side-Angle (ASA): If two angles and the included side of one triangle are congruent to two angles and the included side of another, the triangles are congruent.
- Angle-Angle-Side (AAS): If two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of another, the triangles are congruent.
- Hypotenuse-Leg (HL): In right triangles, if the hypotenuse and one leg of one triangle are congruent to the hypotenuse and one leg of another, the triangles are congruent.
💡 Note: Remember that these postulates are tools, not rules; they're the foundation upon which proofs are built.
1. Start with a Diagram

Visualizing the triangles you’re working with can drastically reduce complexity:
- Draw the triangles accurately and label all given information.
- Include any lines, angles, or labels that might help you recognize congruence.
- Use geometric figures to represent what’s given (e.g., marks for equal sides, arcs for angles).

By having a visual, it becomes easier to spot corresponding parts that might be equal, which can guide your proof.
2. Use Algebra and Properties

Geometry isn’t just about shapes; algebra plays a significant role:
- Identify common algebraic properties like transitivity of congruence, addition, subtraction, or division to relate sides or angles.
- Apply these properties to equalities within the triangles.
For example, if segment AB is equal to segment CD, and segment CD is equal to segment EF, then by transitivity, segment AB is equal to segment EF.
3. Leverage Symmetry and Rotations

Sometimes triangles might appear different but are just rotations or reflections of each other:
- Check if one triangle can be superimposed onto another through rotations or reflections.
- Use these symmetries to establish congruence by demonstrating identical parts.
✨ Note: Symmetry and rotation can simplify proofs by reducing the number of steps needed to show congruence.
4. Practice Deduction from Given Information

One of the core skills in proving congruence is making logical deductions from given information:
- List down what is known from the problem statement or diagram.
- Work backward from the conclusion you want to reach, identifying what needs to be true for that conclusion to be valid.
This backward reasoning often helps in discovering the necessary steps to prove the desired congruence.
5. Incorporate Multiple Congruence Postulates

Understanding when to use which congruence postulate:
- Sometimes you might need to use several postulates or theorems together. For instance, you might use AAS to show one pair of triangles are congruent, then use that result in an SSS proof for another set of triangles.
In summary, mastering triangle congruence proofs involves a blend of geometric intuition, algebraic manipulation, and logical deduction. Here are the key strategies we discussed:
- Understand the Congruence Postulates: This is your foundation. Know what each postulate requires to prove congruence.
- Use Visual Aids: Drawing out diagrams helps visualize the problem, making it easier to spot congruences.
- Apply Algebra: Use algebraic properties to relate parts of triangles.
- Leverage Symmetry: Sometimes, triangles are congruent through simple transformations.
- Make Logical Deductions: Work backward from what you want to prove to guide your proof steps.
With practice, these strategies will not only help you solve triangle congruence proofs more efficiently but also deepen your understanding of geometric concepts.
What if I can’t use any of the basic congruence postulates?

+
Sometimes, you need to use less common theorems like the Side-Angle-Side Angle (SASA) or Vertical Angles Theorem, or look for isosceles or equilateral properties.
Can triangles be congruent if they are not in the same position or orientation?

+
Yes, triangles can be congruent even if they are rotated, flipped, or translated. The key is that corresponding parts match in size and shape.
How can I use congruence to solve other geometry problems?

+
Triangle congruence can be applied to find missing angles, prove parallel lines, or even to solve for the area of triangles by establishing congruent bases or heights.