Triangle Angle Sum: 5 Answers to Boost Your Skills
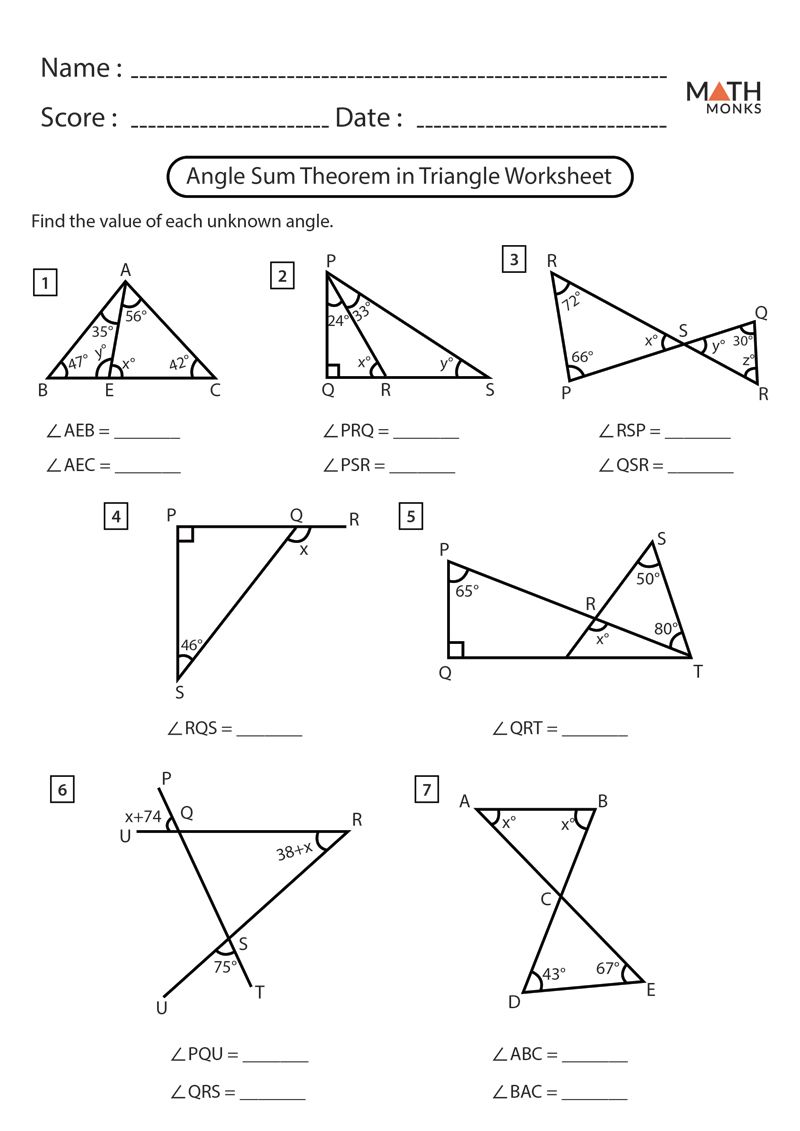
Mathematics is often described as the universal language of the universe, and understanding geometric properties can provide insights into patterns and solutions that are applicable in numerous fields. One fundamental concept in geometry is the Triangle Angle Sum Theorem, which states that the sum of the angles in any triangle always adds up to 180 degrees. This theorem is not only essential for understanding the properties of triangles but also serves as a gateway to deeper exploration in both geometry and trigonometry. Here, we delve into five answers that will help you master this theorem and boost your geometric skills.
The Basics: What is the Triangle Angle Sum Theorem?

Before we can dive into advanced applications, it’s crucial to grasp the basic premise of the theorem. The Triangle Angle Sum Theorem asserts that:
- The sum of the interior angles in a triangle is always 180 degrees.
- Given any triangle ABC, if ∠A, ∠B, and ∠C are the three angles, then ∠A + ∠B + ∠C = 180°.
💡 Note: This theorem holds true for all types of triangles: acute, right, obtuse, isosceles, equilateral, and scalene.
Understanding the Proof


Understanding why the sum of angles in a triangle equals 180° involves recognizing how triangles interact with straight lines:
- Draw a triangle ABC: Imagine any triangle and extend one of its sides beyond the triangle to form a straight line.
- Create another angle: Extend line BC to a point D, forming a straight line with ∠A and another angle, let's call it ∠ADC.
- Sum of angles on a straight line: We know from geometry that the angles on a straight line add up to 180°.
- Relating angles: ∠A + ∠ADC = 180°. Since ∠ADC is an exterior angle, ∠ADC = ∠B + ∠C.
- Conclusion: Therefore, ∠A + (∠B + ∠C) = 180°.
Practical Applications

| Field | Application |
|---|---|
| Surveying | Calculating land plots by ensuring the angles of a triangular plot sum up to 180 degrees. |
| Architecture | Designing stable structures and ensuring roof angles conform to the theorem. |
| Engineering | Analyzing forces in trusses and frameworks by understanding angle relationships. |

Troubleshooting Common Errors

Here are some common mistakes when working with the Triangle Angle Sum Theorem and how to avoid them:
- Misinterpreting exterior angles: Exterior angles are not included in the sum of 180°. Always focus on the interior angles.
- Overlooking supplementary angles: When dealing with straight lines, remember that supplementary angles add up to 180°.
- Ignoring different types of triangles: The theorem applies to all triangles, so ensure not to limit its application to one type.
👉 Note: Always double-check your angles when they don't sum to 180°. There might be an error in measurement or calculation.
Expanding into Trigonometry


Once familiar with the Triangle Angle Sum Theorem, trigonometry opens up new avenues for problem-solving and geometric analysis:
- Right Triangle Trigonometry: Understanding how the angles relate to the sides through sine, cosine, and tangent.
- Law of Sines and Cosines: These laws help solve triangles when you have more complex data.
- Applications in various fields: From physics to navigation, trigonometry provides tools for problem-solving.
🌐 Note: Trigonometry not only builds on the Triangle Angle Sum Theorem but also enhances our ability to solve real-world problems involving angles and distances.
Next Steps in Geometry

Here are some avenues to further explore geometry:
- Study different types of quadrilaterals: Parallelograms, trapezoids, and more; they often require an understanding of triangle properties.
- Investigate polygons: Understanding how to calculate their interior angles using the Triangle Angle Sum Theorem.
- Dive into Non-Euclidean Geometry: Explore how different geometries challenge traditional Euclidean concepts.
By mastering the Triangle Angle Sum Theorem, you're laying down a strong foundation in geometry. This theorem isn't just an isolated rule; it's a key to unlocking vast mathematical and practical knowledge. It helps you understand shapes, predict behavior in physical systems, and solve complex problems with elegance and precision. As we've seen, it's not just about triangles; it's about seeing the interconnectedness of geometric principles and how they can be applied in diverse contexts.
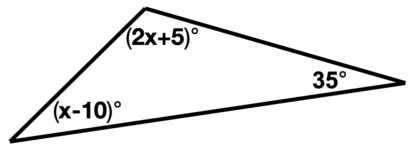
Why does the sum of angles in a triangle always equal 180°?
+
This phenomenon occurs because triangles are inherently flat or Euclidean shapes where the sum of angles on a straight line (which is what an extended triangle side would make) is 180°.
What happens if the angles in a triangle don’t add up to 180°?

+
This situation would suggest a measurement or calculation error or a move into non-Euclidean geometry where the sum of angles might differ from 180°.
Can you use the Triangle Angle Sum Theorem in non-Euclidean geometries?

+
No, this theorem specifically applies to Euclidean geometry. In spherical geometry, for example, the sum of angles is greater than 180°.
How does the Triangle Angle Sum Theorem help in real-world applications?

+
It’s fundamental in fields like architecture for designing stable structures, in surveying for measuring land plots, and in engineering for analyzing forces and stability.